I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on the different definitions on inverse functions that appear in Precalculus and Calculus.
Square Roots, nth Roots, and Rational Exponents
Part 1: Simplifying
Part 2: The difference between and solving
Part 3: Definition of an inverse function and the horizontal line test
Part 4: Why extraneous solutions may occur when solving algebra problems involving a square root
Part 5: Defining
Part 6: Consequences of the definition of : simplifying
Part 7: Defining if
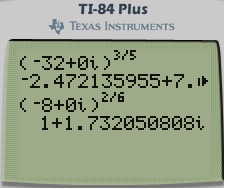
is odd or even
Part 8: Rational exponents if the denominator of the exponent is odd or even
Arcsine
Part 9: There are infinitely many solutions to
Part 10: Defining arcsine with domain
Part 11: Pedagogical thoughts on teaching arcsine.
Part 12: Solving SSA triangles: impossible case
Part 13: Solving SSA triangles: one way of getting a unique solution
Part 14: Solving SSA triangles: another way of getting a unique solution
Part 15: Solving SSA triangles: continuation of Part 14
Part 16: Solving SSA triangles: ambiguous case of two solutions
Part 17: Summary of rules for solving SSA triangles
Arccosine
Part 18: Definition for arccosine with domain
Part 19: The Law of Cosines and solving SSS triangles
Part 20: Identifying impossible triangles with the Law of Cosines
Part 21: The Law of Cosines provides an unambiguous angle, unlike the Law of Sines
Part 22: Finding the angle between two vectors
Part 23: A proof for why the formula in Part 22 works
Arctangent
Part 18: Definition for arctangent with domain
Part 24: Finding the angle between two lines
Part 25: A proof for why the formula in Part 24 works.
Arcsecant
Part 26: Defining arcsecant using
Part 27: Issues that arise in calculus using the domain
Part 28: More issues that arise in calculus using the domain
Part 29: Defining arcsecant using
Logarithm
Part 30: Logarithms and complex numbers