Another Poorly Written Word Problem: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series poorly written word problem, taken directly from textbooks and other materials from textbook publishers.

Part 1: Addition and estimation.

Part 2: Estimation and rounding.

Part 3: Probability.

Part 4: Subtraction and estimation.

Part 5: Algebra and inequality.

Part 6: Domain and range of a function.

Part 7: Algebra and inequality.

Part 8: Algebra and inequality.

Part 9: Geometric series.

Part 10: Currently infeasible track and field problem.

Part 11: Another currently infeasible track and field problem.

Another Poorly Written Word Problem: Index

Part 1: Addition and estimation.

Part 2: Estimation and rounding.

Part 3: Probability.

Part 4: Subtraction and estimation.

Part 5: Algebra and inequality.

Part 6: Domain and range of a function.

Part 7: Algebra and inequality.

Part 8: Algebra and inequality.

Part 9: Geometric series.

Another poorly written word problem (Part 9)

Textbooks have included the occasional awful problem ever since Pebbles Flintstone and Bamm-Bamm Rubble chiseled their homework on slate tablets while attending Bedrock Elementary. But even with the understanding that there have been children have been doing awful homework problems since the dawn of time (and long before the advent of the Common Core), this one is a doozy.

While the ball is on the 20-yard line, a defensive end is suddenly cursed so that he commits a penalty every down that causes the following:

a. The ball is moved half the distance to the goal line, and
b. The down is replayed.

Show that the ball will eventually travel the entire 20-yard distance to the goal.

Sigh. The textbook expects students to use the formula for an infinite geometric series

$\displaystyle \sum_{n=0}^\infty ar^n = \displaystyle \frac{a}{1-r}$

with $a = 10$ and $r = 0.5$ . However, this series only works if there are an infinite number of terms, so that any finite partial sum will be less than 20. Therefore, saying that the ball “will eventually travel” all 20 yards is misleading, as this implies that this happens after a finite amount of time.

Another Poorly Written Word Problem: Index

Part 1: Addition and estimation.

Part 2: Estimation and rounding.

Part 3: Probability.

Part 4: Subtraction and estimation.

Part 5: Algebra and inequality.

Part 6: Domain and range of a function.

Part 7: Algebra and inequality.

Part 8: Algebra and inequality.

Another poorly written word problem (Part 8)

There’s no sense having a debate about standards for elementary mathematics if textbook publishers can’t construct sentences that can be understood by students (or their parents).

On its face, problems 11 and 12 don’t look so bad. For #11, the appropriate inequality is

$1400 + 243 + w \le 2000$

$1643 + w \le 2000$

$w \le 357$

For #12, the inequality is

$7 + g \le 15$

$g \le 8$ .

These indeed are the answers that the textbook is expecting. However, both answers are wrong because both $w$ and $g$ have to be positive. So the answers should be $0 \le w \le 357$ and $0 \le g \le 8$ . Which would be no big deal — except that these problems appeared before compound inequalities were introduced. (Notice that problems 7 through 10 only contain a single inequality.)

So, in a nutshell, the correct answers for these problems require skills that students have not yet learned at the time that they would attempt these problems.

Another poorly written word problem (Part 7)

There’s no sense having a debate about standards for elementary mathematics if textbook publishers can’t construct sentences that can be understood by students (or their parents).

Based only on how the questions are worded, should the answers to #53 and #54 be

$5x - 10 < 6x -8 \qquad \hbox{and} \qquad x + 20 < 4x - 1$ ?

Or should they be

$5x - 10 < 6(x -8) = 6x - 48 \qquad \hbox{and} \qquad x + 20 < 4(x - 1) = 4x -4$ ?

My answer: I have no idea. An argument could be made for either interpretation. And if a problem can be read two different ways by reasonable readers, then it should never be published in a textbook.

Another poorly written word problem (Part 6)

There’s no sense having a debate about standards for elementary mathematics if textbook publishers can’t construct sentences that can be understood by students (or their parents).

This one makes my blood boil. According to its advocates, the whole point of the Common Core standards was to increase the rigor in secondary mathematics. However, this one is SIMPLY WRONG.

The textbook does correctly note that the proper definition of a function is a set of ordered pairs. The “correct” answer, according to the textbook, is answer G — the plotted points do not match the ordered pairs.

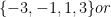However, answer H is also wrong. The textbook would have students believe that order is important when listing the elements of a set. However, order is not important — the domain of $\{-3, 1, -1, 3\}$ is the same as $\{-3, -1, 1, 3\} or$ latex \{3, -3, -1, 1\}$. This is standard mathematical notation — in an ordered pair (or ordered $n-$ tuple), the order is important. For a set, the order is not important.

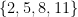Specifying that the domain is $\{-3,-1,1,3\}$ and the range is $\{2,5,8,11\}$ does not uniquely determine the function. In fact, there are 24 different functions that have this domain and range (where we distinguish between the range of a function and its codomain).

In other words, in trying to be clever about properly defining a function and showing different representations of a function, the textbook promotes a misconception about sets… which makes me wonder if the textbook’s attempt at trying to be ultra-careful about the definition of a function is really worth it.

Another poorly written word problem (Part 5)

There’s no sense having a debate about standards for elementary mathematics if textbook publishers can’t construct sentences that can be understood by students (or their parents).

This one really annoys me. The area is less than 55 square inches, and so the appropriate inequality is

$\frac{1}{2} (5)(2x+3) < 55$

$5(2x+3) < 110$

$2x + 3 < 22$

$2x < 19$

$x < 9.5$

However, part (c) asks for the maximum height of the triangle. But there isn’t a maximum possible height. If the height was actually equal to 9.5 inches, then the area would be equal to 55 square inches, which is too big! Also, if any height less than 9.5 is chosen (for the sake of argument, say 9.499), then there is another acceptable height that’s larger (say 9.4995).

Technically, the problem should ask for the greatest upper bound (or supremum) of the height of the triangle, but that’s too much to expect of middle school or high school students learning algebra.

This problem could have been salvaged if it had stated that the area is less than or equal to 55 square inches. However, in its present form, part (c) of this problem is unforgivably awful.

Another poorly written word problem (Part 4)

There’s no sense having a debate about standards for elementary mathematics if textbook publishers can’t write reasonable homework problems.

My reaction to this problem is pretty much echoed by the following post: http://www.patheos.com/blogs/friendlyatheist/2015/10/22/sometimes-estimating-is-better-than-getting-the-exact-answer/:

Yes, this is an awful word problem. This should never have appeared in a math textbook or workbook. But if it appeared in a workbook, then it should never have been assigned by a teacher. And if it accidentally got assigned by a teacher, then the teacher should have extended some grace in the grading of the problem.
Even with all that said, estimation has been in the elementary curriculum for decades and is not an invention of the Common Core. Furthermore, estimation is an important skill for students to acquire. From the above website:

Suppose you’re buying groceries. You have four items in your cart that cost $1.99, $4.93, $6.03, and $5.14.

If all you have is $20 in your wallet, is that enough to pay for the items?

I think that’s a very realistic question.

It would take you at least a little bit of time to add up those numbers individually and get an exact number. Would it answer your question? Absolutely. But you don’t need an exact answer.

The smarter thing to do would be to simply round the numbers. We should be saying to ourselves, “2 + 5 + 6 + 5 equals 18… throw in some tax… and I should still be under $20.”

Why is that better? Because the exact amount doesn’t really make a difference. You just need to be close enough.

I have deep and profound theological differences with the author of this post. But on this math issue, he’s right on the money (pardon the pun).

Another poorly written word problem (Part 3)

There’s no sense having a debate about standards for elementary mathematics if textbook publishers can’t construct sentences that can be understood by elementary students.