Inverse Function

View this post on Instagram

A post shared by Math Memes (@miss_mathmemes)

My Favorite One-Liners: Part 63

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

I’ll use today’s one-liner to explain why mathematicians settled on a particular convention that could have been chosen differently. For example, let’s consider the definition of $y = \sin^{-1} x$ by first looking at the graph of $f(x) = \sin x$ .

Of course, we can’t find an inverse for this function; colloquially, the graph of $f$ fails the horizontal line test. More precisely, there exist two numbers $x_1$ and $x_2$ so that $x_1 \ne x_2$ but $f(x_1) = f(x_2)$ . Indeed, there are infinitely many such pairs.

So how will we find the inverse of $f$ ? Well, we can’t. But we can do something almost as good: we can define a new function $g$ that’s going look an awful lot like $f$ . We will restrict the domain of this new function $g$ so that $g$ satisfies the horizontal line test.

For the sine function, there are plenty of good options from which to choose. Indeed, here are four legitimate options just using the two periods of the sine function shown above. The fourth option is unorthodox, but it nevertheless satisfies the horizontal line test (as long as we’re careful with $\pm 2\pi$ .

So which of these options should we choose? Historically, mathematicians have settled for the interval $[-\pi/2, \pi/2]$ .

So, I’ll ask my students, why have mathematicians chosen this interval? That I can answer with one word: tradition.

For further reading, see my series on inverse functions.

My Favorite One-Liners: Part 16

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

One of the basic notions of functions that’s taught in Precalculus and in Discrete Mathematics is the notion of an inverse function: if $f: A \to B$ is a one-to-one and onto function, then there is an inverse function $f^{-1}: B \to A$ so that

$f^{-1}(f(a)) = a$ for all $a \in A$ and

$f(f^{-1}(b)) = b$ for all $b \in B$ .

If $A = B = \mathbb{R}$ , this is commonly taught in high school as a function that satisfies the horizontal line test.

In other words, if the function $f$ is applied to $a$ , the result is $f(a)$ . When the inverse function is applied to that, the answer is the original number $a$ . Therefore, I’ll tell my class, “By applying the function $f^{-1}$ , we uh-uh-uh-uh-uh-uh-uh-undo it.”

If I have a few country music fans in the class, this always generates a bit of a laugh.

See also the amazing duet with Carrie Underwood and Steven Tyler at the 2011 ACM awards:

My Favorite One-Liners: Part 9

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

Today, I’d like to discuss a common mistake students make in trigonometry… as well as the one-liner that I use to (hopefully) help students not make this mistake in the future.

Question. Find all solutions (rounded to the nearest tenth of a degree) of $\sin x = 0.8$ .

Erroneous Solution. Plugging into a calculator, we find that $x \approx 53.1^o$ .

arcsine1

The student correctly found the unique angle $x$ between $-90^o$ and $90^o$ so that $\sin x = 0.8$ . That’s the definition of the arcsine function. However, there are plenty of other angles whose sine is equal to $0.7$ . This can happen in two ways.

First, if $\sin x > 0$, then the angle $x$ could be in either the first quadrant or the second quadrant (thanks to the mnemonic All Scholars Take Calculus). So $x$ could be (accurate to one decimal place) equal to either $53.1^o$ or else $180^o - 53.1^o = 126.9^o$ . Students can visualize this by drawing a picture, talking through each step of its construction (first black, then red, then brown, then green, then blue).

However, most students don’t really believe that there’s a second angle that works until they see the results of a calculator.

Second, any angle that’s coterminal with either of these two angles also works. This can be drawn into the above picture and, as before, confirmed with a calculator.

So the complete answer (again, approximate to one decimal place) should be $53.1^{\circ} + 360n^o$ and $126.9 + 360n^{\circ}$ , where $n$ is an integer. Since integers can be negative, there’s no need to write $\pm$ in the solution.

Therefore, the student who simply answers $53.1^o$ has missed infinitely many solutions. The student has missed every nontrivial angle that’s coterminal with $53.1^o$ and also every angle in the second quadrant that also works.

Here’s my one-liner — which never fails to get an embarrassed laugh — that hopefully helps students remember that merely using the arcsine function is not enough for solving problems such as this one.

You’ve forgotten infinitely many solutions. So how many points should I take off?

For further reading, here’s my series on inverse functions.

Engaging students: Inverse trigonometric functions

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Joe Wood. His topic, from Precalculus: inverse trigonometric functions.

What are the contributions of various cultures to this topic?

Trig functions have a very long history spanning many countries and cultures. Greek astronomers such as Aristarchus, Claudius, and Ptolemy first used trigonometry; however, according to the University of Connecticut, these Greek astronomers were primarily concerned with “the length of the chord of a circle as a function of the circular arc joining its endpoints.” Many of these astronomers, Ptolemy especially, were concerned with planetary and celestial body’s rotations, so this made sense.

While the Greeks first studied trigonometric concepts, it was the Indian people who really studied sine and cosine functions with the angle as a variable. The information was then brought to the Arabic and Persian cultures. One significant figure, a Persian by the name Abu Rayhan Biruni, used trig to accurately estimate the circumference of Earth and its radius before the end of the 11^th century.

Fast-forward about 700 years, a Swiss mathematician, Daniel Bernoulli, used the “A.sin” notation to represent the inverse of sine. Shortly after, another Swiss mathematician used “A t” to represent the inverse of tangent. That man was none other than Leonhard Euler. It was not until 1813 that the notation sin^-1 and tan^-1 were introduced by Sir John Fredrick William Herschel, an English mathematician.

As we can see, the development of inverse trigonometric functions took quite the cultural rollercoaster ride before stopping some place we see being familiar. It took many cultures, and even more years to develop this sophisticated branch of mathematics.

How could you as a teacher create an activity or project that involves your topic?

Last Semester I taught a lesson on the trigonometric identities. I found this cool cut and paste activity for the students that allowed them to warm up to the trig identities by not having to do the process themselves, but still having to see every step of converting one trig function into another with the identities. Below, you will find the activity, then the instructions, and finally how to modify the activity to fit inverse trig identities specifically.

Directions:
1.) Begin by cutting out all the pieces.
2.) Students will take any of the four puzzle pieces with the black squiggly line.
3.) Find an equivalent puzzle piece by using some trig identity.
4.) Repeat step 3 until there are no more equivalent pieces.
5.) Grab the next puzzle pieces with the black squiggly line.
6.) Repeat steps 3-5 until all puzzle pieces have been used.
Ex.) Begin with cscx-sinx. Lay next to that piece, the piece that reads =1/sinx – sinx, then the piece that reads =1/sinx – sin²x/sinx. Contiue the trend until you reach =cotx * cosx. Then move to the next squiggly lined piece.

Modify:
This game can be modified using inverse trig functions. Start with pieces such as sin^-1(sin(30⁰)) in squiggles. Have a piece showing sin^-1(sin(30⁰)) with a line through the sines. Then a piece that just shows 30⁰. Next a piece in a squiggly line that is sin^-1(sqrt(2)/2) that connects to a piece of 45⁰, but make them write why this works.

How does this topic extend what your students should have learned in previous courses?

Obviously, by this time students should know what trigonometric functions are and how to use this. Students should also know from previous classes what inverse functions are. Studying inverse trig functions then is a continuation of these topics. As I teacher I would begin relating inverse trig functions by refreshing the students on what inverse functions are. The class would then move into the concept that the trig expression of an angle returns a ratio of two sides of a triangle. We would slowly move into what happens then if you know the sides of a triangle but need the angle. From there we would discuss trigonometric expressions using the angles as variables. Finally, we would make the connection that that is a function, and on the proper interval should have an inverse function. That is when the extension into the new topic of inverse trigonometric functions would seriously begin.

Undo It

$f^{-1}(f(a)) = a$ for all $a \in A$ and

$f(f^{-1}(b)) = b$ for all $b \in B$ .

If $A = B = \mathbb{R}$ , this is commonly taught in high school as a function that satisfies the horizontal line test.

If I have a few country music fans in the class, this always generates a bit of a laugh.

See also the amazing duet with Carrie Underwood and Steven Tyler at the 2011 ACM awards:

Engaging students: Computing inverse functions

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Carissa Birdsong. Her topic, from Algebra: computing inverse functions.

How can this topic be used in your students’ future courses in mathematics or science?

When students are learning any algorithm in math, it helps keep their interest if they know what this can be possibly used for in the future. In pre-calculus, students need to find the inverse of cosine, sine, tangent, etc. to find certain angles. In order to grasp the students’ attention, the teacher can show videos of bottle rockets being shot off at different angles. Then the teacher will explain that in order to find most of these angles, one must use the inverse property. Then the teacher can go into depth of how to find the inverse of a function. But, the students must understand that using inverse to find angle measurements will not happen in this curriculum, but in future classes such as pre-calculus, trigonometry and physics.

How could you as a teacher create an activity or project that involves your topic?

Human Representation of Inverse Function

Move the desks to the sides of the room, making a big open space in the middle.
Assign each student a partner.
Have a strip of tape down the middle of the room prior to class. Have the students line up facing their partner with the strip of tape in between them.
Have the side on the “right” be side A and the side on the “left” be side B. (The teacher will choose which side is the right or left, depending on where the front of the classroom is)
Side A will pick a position to stand in (the teacher must monitor to make sure the students are being appropriate). The students are encouraged to change their face, arms, head, etc. to pick the most creative position possible.
Now side B will mimic their specific partner on side A.
Once the students have locked in their position, the teacher will point out that side B is reflective of side A. Therefore, side B is the inverse function of A.

*Make sure that the students understand that side B is not doing the exact same thing that side A is doing, but the opposite, the reflection. The inverse of a function “undoes” the function itself. If someone were to take away side A, and bring in a new crop of people to reflect side B, it should be EXACTLY what side A had done. The inverse of the inverse of a function must take you back to the original function.

*After the teacher teaches how to find the inverse of a function, and can elaborate on the graphing of each function, he or she can refer back to this activity and show that there is an invisible line between the function and the inverse function, making clear that they reflect each other, just as the students did.

How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?

Even though most students probably haven’t seen Top Secret, they will probably appreciate watching any sort of movie or television during class. In the making of Top Secret, the actors film a scene walking backwards and saying lines in reverse order. In the movie, this scene is played in reverse, so they look like they were just speaking gibberish and walking forward. They did this so Val Kilmer can do cool tricks like throw a book on the top shelve and slide up a pole.

The teacher could show his or her class the original scene, straight from the movie.

Then ask, “How do you think the actors did this?” “What language are they speaking?” Hopefully a student will catch on fast and say that they just filmed it backwards. Then the teacher can show the scene played forwards.

These two scenes are inverse each other. Going from the beginning to the end of one takes you to the beginning of the other. And going from the beginning to the end of the other, takes you to the beginning of one. Most functions have an inverse function. This means there is a function that is reverse of its inverse. This does NOT mean that the inverse of a function is just the original backwards (i.e. y=3+x and x+3=y). The function of f has the input x and the output y, whereas the inverse of the function f has the input y and the output x.

Resources:

https://www.youtube.com/watch?v=jXlucE4iUDE

https://www.youtube.com/watch?v=2Mr_XAM8CMw

Inverse Functions: Index

I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on the different definitions on inverse functions that appear in Precalculus and Calculus.

Square Roots, nth Roots, and Rational Exponents

Part 1: Simplifying $\sqrt{x^2}$

Part 2: The difference between $\sqrt{t}$ and solving $x^2 = t$

Part 3: Definition of an inverse function and the horizontal line test

Part 4: Why extraneous solutions may occur when solving algebra problems involving a square root

Part 5: Defining $\sqrt{x}$

Part 6: Consequences of the definition of $\sqrt{x}$ : simplifying $\sqrt{x^2}$

Part 7: Defining $\sqrt[n]{x}$ if $n$ is odd or even

Part 8: Rational exponents if the denominator of the exponent is odd or even

Arcsine

Part 9: There are infinitely many solutions to $\sin x = 0.8$

Part 10: Defining arcsine with domain $[-\pi/2,\pi/2]$

Part 11: Pedagogical thoughts on teaching arcsine.

Part 12: Solving SSA triangles: impossible case

Part 13: Solving SSA triangles: one way of getting a unique solution

Part 14: Solving SSA triangles: another way of getting a unique solution

Part 15: Solving SSA triangles: continuation of Part 14

Part 16: Solving SSA triangles: ambiguous case of two solutions

Part 17: Summary of rules for solving SSA triangles

Arccosine

Part 18: Definition for arccosine with domain $[0,\pi]$

Part 19: The Law of Cosines and solving SSS triangles

Part 20: Identifying impossible triangles with the Law of Cosines

Part 21: The Law of Cosines provides an unambiguous angle, unlike the Law of Sines

Part 22: Finding the angle between two vectors

Part 23: A proof for why the formula in Part 22 works

Arctangent

Part 18: Definition for arctangent with domain $(-\pi/2,\pi/2)$

Part 24: Finding the angle between two lines

Part 25: A proof for why the formula in Part 24 works.

Arcsecant

Part 26: Defining arcsecant using $[0,\pi/2) \cup (\pi/2,\pi]$

Part 27: Issues that arise in calculus using the domain $[0,\pi/2) \cup (\pi/2,\pi]$

Part 28: More issues that arise in calculus using the domain $[0,\pi/2) \cup (\pi/2,\pi]$

Part 29: Defining arcsecant using $[0,\pi/2) \cup [pi,3\pi/2)$

Logarithm

Part 30: Logarithms and complex numbers

Inverse Functions: Logarithms and Complex Numbers (Part 30)

Ordinarily, there are no great difficulties with logarithms as we’ve seen with the inverse trigonometric functions. That’s because the graph of $y = a^x$ satisfies the horizontal line test for any $0 < a < 1$ or $a > 1$ . For example,

$e^x = 5 \Longrightarrow x = \ln 5$ ,

and we don’t have to worry about “other” solutions.

However, this goes out the window if we consider logarithms with complex numbers. Recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta) = r e^{i \theta}$

where $r = |z| = \sqrt{a^2 + b^2}$ and $\tan \theta = b/a$ , with $\theta$ in the appropriate quadrant. This is analogous to converting from rectangular coordinates to polar coordinates.

Over the past few posts, we developed the following theorem for computing $e^z$ in the case that $z$ is a complex number.

Definition. Let $z = r e^{i \theta}$ be a complex number so that $-\pi < \theta \le \theta$ . Then we define

$\log z = \ln r + i \theta$ .

Of course, this looks like what the definition ought to be if one formally applies the Laws of Logarithms to $r e^{i \theta}$ . However, this complex logarithm doesn’t always work the way you’d think it work. For example,

$\log \left(e^{2 \pi i} \right) = \log (\cos 2\pi + i \sin 2\pi) = \log 1 = \ln 1 = 0 \ne 2\pi i$ .

This is analogous to another situation when an inverse function is defined using a restricted domain, like

$\sqrt{ (-3)^2 } = \sqrt{9} = 3 \ne -3$

$\sin^{-1} (\sin \pi) = \sin^{-1} 0 = 0 \ne \pi$ .

The Laws of Logarithms also may not work when nonpositive numbers are used. For example,

$\log \left[ (-1) \cdot (-1) \right] = \log 1 = 0$ ,

but

$\log(-1) + \log(-1) = \log \left( e^{\pi i} \right) + \log \left( e^{\pi i} \right) = \pi i + \pi i = 2\pi i$ .

This material appeared in my previous series concerning calculators and complex numbers: https://meangreenmath.com/2014/07/09/calculators-and-complex-numbers-part-21/

Inverse Functions: Arcsecant (Part 29)

We now turn to a little-taught and perhaps controversial inverse function: arcsecant. As we’ve seen throughout this series, the domain of this inverse function must be chosen so that the graph of $y = \sec x$ satisfies the horizontal line test. It turns out that the choice of domain has surprising consequences that are almost unforeseeable using only the tools of Precalculus.

The standard definition of $y = \sec^{-1} x$ uses the interval $[0,\pi]$ — or, more precisely, $[0,\pi/2) \cup (\pi/2, \pi]$ to avoid the vertical asymptote at $x = \pi/2$ — in order to approximately match the range of $\cos^{-1} x$ . However, when I was a student, I distinctly remember that my textbook chose $[0,\pi/2) \cup [\pi,3\pi/2)$ as the range for $\sec^{-1} x$ .

I believe that this definition has fallen out of favor today. However, for the purpose of today’s post, let’s just run with this definition and see what happens. This portion of the graph of $y = \sec x$ is perhaps unorthodox, but it satisfies the horizontal line test so that the inverse function can be defined.

Let’s fast-forward a couple of semesters and use implicit differentiation (see also https://meangreenmath.com/2014/08/08/different-definitions-of-logarithm-part-8/ for how this same logic is used for other inverse functions) to find the derivative of $y = \sec^{-1} x$ :

$x = \sec y$

$\displaystyle \frac{d}{dx} (x) = \displaystyle \frac{d}{dx} (\sec y)$

$1 = \sec y \tan y \displaystyle \frac{dy}{dx}$

$\displaystyle \frac{1}{\sec y \tan y} = \displaystyle \frac{dy}{dx}$

At this point, the object is to convert the left-hand side to something involving only $x$ . Clearly, we can replace $\sec y$ with $x$ . As it turns out, the replacement of $\tan y$ is a lot simpler than we saw in yesterday’s post. Once again, we begin with one of the Pythagorean identities:

$1 + \tan^2 y = \sec^2 y$

$\tan^2 y = \sec^2 y - 1$

$\tan^2 y = x^2 - 1$

$\tan y = \sqrt{x^2 - 1} \qquad \hbox{or} \tan y = -\sqrt{x^2 - 1}$

So which is it, the positive answer or the negative answer? In yesterday’s post, the answer depended on whether $x$ was positive or negative. However, with the current definition of $\sec^{-1} x$ , we know for certain that the answer is the positive one! How can we be certain? The angle $y$ must lie in either the interval $[0,\pi/2)$ or else the interval $[\pi,3\pi/2)$ . In either interval, $\tan y$ is positive. So, using this definition of $\sec^{-1} x$ , we can simply say that

$\displaystyle \frac{d}{dx} \sec^{-1} x = \displaystyle \frac{1}{x \sqrt{x^2-1}}$ ,

and we don’t have to worry about $|x|$ that appeared in yesterday’s post.

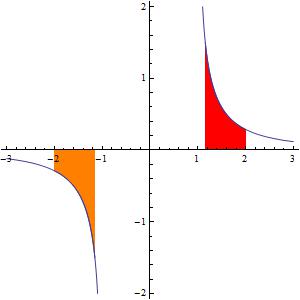Turning to integration, we now have the simple formula

$\displaystyle \int \frac{dx}{x \sqrt{x^2 -1}} = \sec^{-1} x + C$

that works whether $x$ is positive or negative. For example, the orange area can now be calculated correctly:

$\displaystyle \int_{-2}^{-2\sqrt{3}/3} \frac{dx}{x \sqrt{x^2 -1}} = \sec^{-1} \left( - \displaystyle \frac{2\sqrt{3}}{3} \right) - \sec^{-1} (-2)$

$= \displaystyle \frac{7\pi}{6} - \frac{4\pi}{3}$

$= \displaystyle -\frac{\pi}{6}$

So, unlike yesterday’s post, this definition of $\sec^{-1} x$ produces a simple integration formula.

So why isn’t this the standard definition for $\sec^{-1} x$ ? I’m afraid the answer is simple: with this definition, the equation

$\sec^{-1} x = \cos^{-1} \left( \displaystyle \frac{1}{x} \right)$

is no longer correct if $x < -1$ . Indeed, I distinctly remember thinking, back when I was a student taking trigonometry, that the definition of $\sec^{-1} x$ seemed really odd, and it seemed to me that it would be better if it matched that of $\cos^{-1} x$ . Of course, at that time in my mathematical development, it would have been almost hopeless to explain that the range $[0,\pi/2) \cup [\pi,3\pi/2)$ had been chosen to simplify certain integrals from calculus.

So I suppose that The Powers That Be have decided that it’s more important for this identity to hold than to have a simple integration formula for $\displaystyle \int \frac{dx}{x \sqrt{x^2 -1}}$