My Favorite One-Liners: Part 111

I tried a new wise-crack in class recently, and it was a rousing success. My math majors had trouble recalling basic facts about tests for convergent and divergent series, and so I projected onto the front screen the Official Repository of all Knowledge (www.google.com) and searched for “divergent series” to “help” them recall their prior knowledge.

Worked like a charm.

https://www.google.com/search?q=divergent+series

My Favorite One-Liners: Part 35

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

Every once in a while, I’ll discuss something in class which is at least tangentially related to an unsolved problems in mathematics. For example, when discussing infinite series, I’ll ask my students to debate whether or not this series converges:

$1 + \frac{1}{10} + \frac{1}{100} + \frac{1}{1000} + \dots$

Of course, this one converges since it’s an infinite geometric series. Then we’ll move on to an infinite series that is not geometric:

$1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \dots$ ,

where the denominators are all perfect squares. I’ll have my students guess about whether or not this one converges. It turns out that it does, and the answer is exactly what my students should expect the answer to be, $\pi^2/6$ .

Then I tell my students, that was a joke (usually to relieved laughter).

Next, I’ll put up the series

$1 + \frac{1}{8} + \frac{1}{27} + \frac{1}{64} + \dots$ ,

where the denominators are all perfect cubes. I’ll have my students guess about whether or not this one converges. Usually someone will see that this one has to converge since the previous one converged and the terms of this one are pairwise smaller than the previous series — an intuitive use of the Dominated Convergence Test. Then, I’ll ask, what does this converge to?

The answer is, nobody knows. It can be calculated to very high precision with modern computers, of course, but it’s unknown whether there’s a simple expression for this sum.

So, concluding the story whenever I present an unsolved problem, I’ll tell my students,

If you figure out the answer, call me, and call me collect.

My Favorite One-Liners: Part 12

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

Often in mathematics, one proof is quite similar to another proof. For example, in Precalculus or Discrete Mathematics, students encounter the theorem

$\sum_{k=1}^n (a_k + b_k) = \sum_{k=1}^n a_k + \sum_{k=1}^n b_k$ .

The formal proof requires mathematical induction, but the “good enough” proof is usually convincing enough for most students, as it’s just the repeated use of the commutative and associative properties to rearrange the terms in the sum:

$\sum_{k=1}^n (a_k + b_k)= (a_1 + b_1) + (a_2 + b_2) + \dots + (a_n + b_n)$

$= (a_1 + a_2 + \dots + a_n) + (b_1 + b_2 + \dots + b_n)$

$= \sum_{k=1}^n a_k + \sum_{k=1}^n b_k$ .

Next, I’ll often present the new but closely related theorem

$\sum_{k=1}^n (a_k - b_k) = \sum_{k=1}^n a_k -\sum_{k=1}^n b_k$ .

The proof of this would take roughly the same amount of time as the first proof, but there’s often little pedagogical value in doing all the steps over again in class. So here’s the line I’ll use: “At this point, I invoke the second-most powerful word in mathematics…” and then let them guess what this mysterious word is.

After a few seconds, I tell them the answer: “Similar.” The proof of the second theorem exactly parallels the proof of the first except for some sign changes. So I’ll tell them that mathematicians often use this word in mathematical proofs when it’s dead obvious that the proof can be virtually copied-and-pasted from a previous proof.

Eventually, students will catch on to my deliberate choice of words and ask, “What the most powerful word in mathematics?” As any mathematician knows, the most powerful word in mathematics is “Trivial”… the proof is so easy that it’s not necessary to write the proof down. But I warn my students that they’re not allowed to use this word when answering exam questions.

The third most powerful phrase in mathematics is “It is left for the student,” thus saving the professor from writing down the proof in class and encouraging students to figure out the details on their own.

What I Learned by Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post.

When I was researching for my series of posts on conditional convergence, especially examples related to the constant 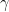$\gamma$ , the reference Gamma: Exploring Euler’s Constant by Julian Havil kept popping up. Finally, I decided to splurge for the book, expecting a decent popular account of this number. After all, I’m a professional mathematician, and I took a graduate level class in analytic number theory. In short, I don’t expect to learn a whole lot when reading a popular science book other than perhaps some new pedagogical insights.

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites along with the page numbers in the book — while giving the book a very high recommendation.

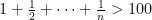Part 1: The smallest value of $n$ so that $1 + \frac{1}{2} + \dots + \frac{1}{n} > 100$ (page 23).

Part 2: Except for a couple select values of $m<n$ , the sum $\frac{1}{m} + \frac{1}{m+1} + \dots + \frac{1}{n}$ is never an integer (pages 24-25).

Part 3: The sum of the reciprocals of the twin primes converges (page 30).

Part 4: Euler somehow calculated $\zeta(26)$ without a calculator (page 41).

Part 5: The integral called the Sophomore’s Dream (page 44).

Part 6: St. Augustine’s thoughts on mathematicians — in context, astrologers (page 65).

Part 7: The probability that two randomly selected integers have no common factors is $6/\pi^2$ (page 68).

Part 8: The series for quickly computing 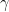$\gamma$ to high precision (page 89).

Part 9: An observation about the formulas for $1^k + 2^k + \dots + n^k$ (page 81).

Part 10: A lower bound for the gap between successive primes (page 115).

Part 11: Two generalizations of 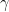$\gamma$ (page 117).

Part 12: Relating the harmonic series to meteorological records (page 125).

Part 13: The crossing-the-desert problem (page 127).

Part 14: The worm-on-a-rope problem (page 133).

Part 15: An amazingly nasty formula for the $n$ th prime number (page 168).

Part 16: A heuristic argument for the form of the prime number theorem (page 172).

Part 17: Oops.

Part 18: The Riemann Hypothesis can be stated in a form that can be understood by high school students (page 207).

Lessons from teaching gifted elementary school students: Index (updated)

I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on various lessons I’ve learned while trying to answer the questions posed by gifted elementary school students. (This is updated from my previous index.)

Part 1: A surprising pattern in some consecutive perfect squares.

Part 2: Calculating 2 to a very large exponent.

Part 3a: Calculating 2 to an even larger exponent.

Part 3b: An analysis of just how large this number actually is.

Part 4a: The chance of winning at BINGO in only four turns.

Part 4b: Pedagogical thoughts on one step of the calculation.

Part 4c: A complicated follow-up question.

Part 5a: Exponentiation is multiplication as multiplication is to addition. So, multiplication is to addition as addition is to what? (I offered the answer of incrementation, but it was rejected: addition requires two inputs, while incrementation only requires one.)

Part 5b: Why there is no binary operation that completes the above analogy.

Part 5c: Knuth’s up-arrow notation for writing very big numbers.

Part 5d: Graham’s number, reputed to be the largest number ever to appear in a mathematical proof.

Part 6a: Calculating $(255/256)^x$.

Part 6b: Solving $(255/256)^x = 1/2$ without a calculator.

Part 7a: Estimating the size of a 1000-pound hailstone.

Part 7b: Estimating the size a 1000-pound hailstone.

Part 8a: Statement of an usually triangle summing problem.

Part 8b: Solution using binomial coefficients.

Part 8c: Rearranging the series.

Part 8d: Reindexing to further rearrange the series.

Part 8e: Rewriting using binomial coefficients again.

Part 8f: Finally obtaining the numerical answer.

Part 8g: Extracting the square root of the answer by hand.

What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 18

The Riemann Hypothesis (see here, here, and here) is perhaps the most famous (and also most important) unsolved problems in mathematics. Gamma (page 207) provides a way of writing down this conjecture in a form that only uses notation that is commonly taught in high school:

If $\displaystyle \sum_{r=1}^\infty \frac{(-1)^r}{r^a} \cos(b \ln r) = 0$ and $\displaystyle \sum_{r=1}^\infty \frac{(-1)^r}{r^a} \sin(b \ln r) = 0$ for some pair of real numbers $a$ and $b$ , then $a = \frac{1}{2}$ .

As noted in the book, “It seems extraordinary that the most famous unsolved problem in the whole of mathematics can be phrased so that it involves the simplest of mathematical ideas: summation, trigonometry, logarithms, and [square roots].”

When I researching for my series of posts on conditional convergence, especially examples related to the constant $\gamma$ , the reference Gamma: Exploring Euler’s Constant by Julian Havil kept popping up. Finally, I decided to splurge for the book, expecting a decent popular account of this number. After all, I’m a professional mathematician, and I took a graduate level class in analytic number theory. In short, I don’t expect to learn a whole lot when reading a popular science book other than perhaps some new pedagogical insights.

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.

What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 15

I did not know — until I read Gamma (page 168) — that there actually is a formula for generating $n$ th prime number by directly plugging in $n$ . The catch is that it’s a mess:

$p_n = 1 + \displaystyle \sum_{m=1}^{2^n} \left[ n^{1/n} \left( \sum_{i=1}^m \cos^2 \left( \pi \frac{(i-1)!+1}{i} \right) \right)^{-1/n} \right]$ ,

where the outer brackets $[~ ]$ represent the floor function.

This mathematical curiosity has no practical value, as determining the 10th prime number would require computing $1 + 2 + 3 + \dots + 2^{10} = 524,800$ different terms!

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.

What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 14

I hadn’t heard of the worm-on-a-rope problem until I read Gamma (page 133). From Cut-The-Knot:

A worm is at one end of a rubber rope that can be stretched indefinitely. Initially the rope is one kilometer long. The worm crawls along the rope toward the other end at a constant rate of one centimeter per second. At the end of each second the rope is instantly stretched another kilometer. Thus, after the first second the worm has traveled one centimeter, and the length of the rope has become two kilometers. After the second second, the worm has crawled another centimeter and the rope has become three kilometers long, and so on. The stretching is uniform, like the stretching of a rubber band. Only the rope stretches. Units of length and time remain constant.

It turns out that, after $n$ seconds, that the fraction of the band that the worm has traveled is $H_n/N$ , where

$H_n = \displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}$

and $N$ is the length of the rope in centimeters. Using the estimate $H_n \approx \ln n + \gamma$ , we see that the worm will reach the end of the rope when

$H_n = N$

$\ln n + \gamma \approx N$

$\ln n \approx N - \gamma$

$n \approx e^{N - \gamma}$ .

If $N = 100,000$ (since the rope is initially a kilometer long), it will take a really long time for the worm to reach its destination!

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.

What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 13

I hadn’t heard of the crossing-the-desert problem until I read Gamma (page 127). From Wikipedia:

There are n units of fuel stored at a fixed base. The jeep can carry at most 1 unit of fuel at any time, and can travel 1 unit of distance on 1 unit of fuel (the jeep’s fuel consumption is assumed to be constant). At any point in a trip the jeep may leave any amount of fuel that it is carrying at a fuel dump, or may collect any amount of fuel that was left at a fuel dump on a previous trip, as long as its fuel load never exceeds 1 unit…

The jeep must return to the base at the end of every trip except for the final trip, when the jeep travels as far as it can before running out of fuel…

[T]he objective is to maximize the distance traveled by the jeep on its final trip.

The answer is, if $n$ fuel dumps are used, the jeep can go a distance of

$H_n = \displaystyle 1 + \frac{1}{3} + \frac{1}{5} + \dots + \frac{1}{2n-1}$ .

Since the right-hand side approaches infinity as $n$ gets arbitrarily large, it is possible to cross an arbitrarily long desert according the rules of this problem.

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.

What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 12

Let $X_1, X_2, X_3, \dots$ be a sequence of independent and identically distributed random variables, and let $H_n$ be the number of “record highs” upon to and including event $n$ . For example, each $X_i$ can represent the amount of rainfall in a year, where $X_1$ is amount of rainfall recorded the first time that records were kept. As shown in Gamma (page 125), the expected number of record highs is

$H_n = \displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}$ .

As noted in Gamma,

Two arbitrary chosen examples are revealing. The Radcliffe Meteorological Station in Oxford has data for rainfall in Oxford between 1767 and 2000 and there are five record years; this is a span of 234 recorded years and $H_{234} = 6.03$ . For Central Park, New York City, between 1835 and 1994 there are six record years over the 160-year period and $H_{160} = 5.65$ , providing good evidence that English weather is that bit more unpredictable.

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.