Factoring Mersenne “primes”

I love hearing and telling tales of legendary mathematicians. Today’s tale comes from Frank Nelson Cole and definitely comes from the era before calculators or computers. From Wikipedia:

On October 31, 1903, Cole famously made a presentation to a meeting of the American Mathematical Society where he identified the factors of the Mersenne number 2⁶⁷ − 1, or M₆₇. Édouard Lucas had demonstrated in 1876 that M₆₇ must have factors (i.e., is not prime), but he was unable to determine what those factors were. During Cole’s so-called “lecture”, he approached the chalkboard and in complete silence proceeded to calculate the value of M₆₇, with the result being 147,573,952,589,676,412,927. Cole then moved to the other side of the board and wrote 193,707,721 × 761,838,257,287, and worked through the tedious calculations by hand. Upon completing the multiplication and demonstrating that the result equaled M₆₇, Cole returned to his seat, not having uttered a word during the hour-long presentation. His audience greeted the presentation with a standing ovation. Cole later admitted that finding the factors had taken “three years of Sundays.”

My Favorite One-Liners: Part 92

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

This is one of my favorite quote from Alice in Wonderland that I’ll use whenever discussing the difference between the ring axioms (integers are closed under addition, subtraction, and multiplication, but not division) and the field axioms (closed under division except for division by zero):

‘I only took the regular course [in school,’ said the Mock Turtle.]

‘What was that?’ inquired Alice.

‘Reeling and Writhing, of course, to begin with,’ the Mock Turtle replied; ‘and then the different branches of Arithmetic — Ambition, Distraction, Uglification, and Derision.’

Abbott and Costello and division

See also the similar post by Ma and Pa Kettle.

Seventy Times Seven

I normally hate these math-is-hard jokes, but this one made me laugh. Forgiving somebody is harder than computing $70 \times 7$ ?

I don’t know who created this cartoon; I’ll be happy to credit it if anybody knows.

Teaching multiplication

I absolutely love this. There’s more to teaching multiplication than rote memorization, but this is wonderful reinforcement for what happens inside of a classroom.

And also this:

Source: https://www.facebook.com/RealDLHughley/photos/a.247216605320684.53846.219856014723410/1096551810387155/?type=3&theater

My Mathematical Magic Show: Part 5d

Last March, on Pi Day (March 14, 2015), I put together a mathematical magic show for the Pi Day festivities at our local library, compiling various tricks that I teach to our future secondary teachers. I was expecting an audience of junior-high and high school students but ended up with an audience of elementary school students (and their parents). Still, I thought that this might be of general interest, and so I’ll present these tricks as well as the explanations for these tricks in this series. From start to finish, this mathematical magic show took me about 50-55 minutes to complete. None of the tricks in this routine are original to me; I learned each of these tricks from somebody else.

Though this wasn’t part of my Pi Day magic show, I recently read an interesting variant on my fourth trick. The next time I do a mathematical show, I’ll do this trick next — not to amaze and stun my audience, but to see if my audience can figure out why it works. Each member of the audience will need to have a calculator (a basic four-function calculator will suffice). Here’s the patter:

I want you to take out your calculator. Using only the digits 1 through 9, there are three rows, three columns, and two diagonals. I want you to pick either a row, a column, or a diagonal. Then I want you to enter a three digit number using those numbers. For example, if you chose the first row, you can enter 123 or 312 or 231 or any three-digit number using each digit once.

Now, I want you to multiply this number by another three-digit number. So hit the times button.

(pause)

Now, choose another row, column, or diagonal and type in another three-digit number, using each of the three digits once.

(pause)

Now hit the equals button to multiply those two numbers together.

(pause)

Is everyone done? The product you just computed should have either five or six digits. I want you to concentrate on one of those digits. Just make sure that you concentrate on a digit other than zero, because zero is boring. So concentrate on a nonzero digit.

(pause)

(I point to someone.) Without telling me the digit you chose, please tell me the other digits in your product.

The audience member will say something like, “3, 7, 9, and 2.” To which I’ll reply in three seconds or less, “The number you chose was 6.”

Then I’ll turn to someone else and ask which numbers were not scratched out. She’ll say something like, “1, 1, 9, 7, and 2.” I’ll answer, “The number you chose was 7.”

And then I’ll repeat this a few times, and everyone’s amazed that I knew the different numbers that were chosen.

Clearly this works using the same logic as my fourth magic trick: the product is always a multiple of 9, and so I can add the digits to figure out the missing digit. The more interesting question is: Why is the product always a multiple of 9?

This works because each of the factors of the product is a multiple of 3. Let’s take another look at the calculator.

If the first row is chosen, the sum of the digits is 1+2+3 = 6, a multiple of 3. And it doesn’t matter if the number is 123 or 312 or 231… the order of the digits is unimportant.

If the second row is chosen, the sum of the digits is 4+5+6 = 15, a multiple of 3.

If the third row is chosen, the sum of the digits is 7+8+9 = 24, a multiple of 3.

If the first column is chosen the sum of the digits is 1+4+7=12, a multiple of 3.

If the second column is chosen, the sum of the digits is 2+5+8 = 15, a multiple of 3.

If the third column is chosen, the sum of the digits is 3+6+9 = 18, a multiple of 3.

If one diagonal is chosen, the sum of the digits is 1+5+9 = 15, a multiple of 3.

If the other diagonal is chosen, the sum of the digits is 3+5+7 = 15, a multiple of 3.

This can be stated more succinctly using algebra. The digits in each row, column, and diagonal form an arithmetic sequence. For each row, the common difference is 1. For each column, the common difference is 3. And for a diagonal, the common difference is either 2 or 4. If I let $a$ be the first term in the sequence and let $d$ be the common difference, then the three digits are $a$ , $a + d$ , and $a + 2d$ , and their sum is

$a + (a+d) + (a+ 2d) = 3a + 3d = 3(a+d)$ ,

which is a multiple of 3. (Indeed, the sum is 3 times the middle number.)

So each factor is a multiple of 3. That means the product has to be a multiple of $9$ . In other words, if the first factor is $3m$ and the second factor is $3n$ , where $m$ and $n$ are integers, their product is equal to

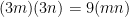$(3m)(3n) = 9(mn)$ ,

which is clearly a multiple of 9. Therefore, I can use the same adding-the-digits trick to identify the missing digit.

My Mathematical Magic Show: Part 5c

I want you to take out your calculator. Using only the digits 1 through 9, there are three rows, three columns, and two diagonals. I want you to pick either a row, a column, or a diagonal. Then I want you to enter a three digit number using those numbers. For example, if you chose the first row, you can enter 123 or 312 or 231 or any three-digit number using each digit once.

Now, I want you to multiply this number by another three-digit number. So hit the times button.

(pause)

Now, choose another row, column, or diagonal and type in another three-digit number, using each of the three digits once.

(pause)

Now hit the equals button to multiply those two numbers together.

(pause)

Is everyone done? The product you just computed should have either five or six digits. I want you to concentrate on one of those digits. Just make sure that you concentrate on a digit other than zero, because zero is boring. So concentrate on a nonzero digit.

(pause)

(I point to someone.) Without telling me the digit you chose, please tell me the other digits in your product.

The audience member will say something like, “3, 7, 9, and 2.” To which I’ll reply in three seconds or less, “The number you chose was 6.”

Then I’ll turn to someone else and ask which numbers were not scratched out. She’ll say something like, “1, 1, 9, 7, and 2.” I’ll answer, “The number you chose was 7.”

And then I’ll repeat this a few times, and everyone’s amazed that I knew the different numbers that were chosen.

Clearly this works using the same logic as yesterday’s post: the product is always a multiple of 9, and so I can add the digits to figure out the missing digit. The more interesting question is: Why is the product always a multiple of 9? I’ll address this in tomorrow’s post.

Multiplication and Animaniacs

One of my guilty pleasures in the 1990s, when I was far too old to be watching children’s cartoons, was the fantastic show “Animaniacs.” In the clip below, Yakko Warner describes how to multiply 47 and 83.

Arithmetic with big numbers: Index

I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on doing basic arithmetic with very large numbers that exceed the character displays of most calculators.

Part 1: Addition

Part 2: Multiplication

Part 3: Division

Math Coach’s Corner

I found the following blogpost very intriguing. This sounds like an engaging way of teaching children how to multiply, whether or not the Common Core was the educational fashion of the day: http://mathcoachscorner.blogspot.com/2014/08/a-peek-inside-theres-nothing-alien.html.