Posted in honor of the upcoming North American solar eclipse.

Source: https://xkcd.com/2769
Explaining the "whys" of mathematics
A brief aside from the current series on general relativity — and the mysterious 43 seconds of arc per century in Mercury’s orbit — that turned into further discussion about angle measurement.
A few months ago, I received this clever postcard from someone visiting Spokane, Washington. The sender clearly knew the recipient (me) well: rather than sending me a postcard showing the jaw-dropping beauty of the Spokane area, I was impressed with the mathematical precision given for Spokane’s location.

I started wondering about exactly how precisely the postcard was measuring the location of Spokane — was it the location of City Hall or some other important landmark? — and I went to Google Maps to find out. (For what it’s worth, xkcd had a comic about this some time ago.)
And then it finally hit me, after far longer than it should have taken, that the postcard is utterly nonsensical.
We would never say that someone’s height is 4 feet, 20 inches. There are 12 inches in a foot, and so we would instead say that the height is 5 feet, 8 inches.
Likewise, when specifying an angle with minutes and seconds, there are (just like with ordinary time) 60 seconds in a minute and 60 minutes in a degree (so that there are 3600 seconds in a degree). Therefore, specifying an angle with 67′ or 66″, as in the postcard, makes absolutely no sense.
Furthermore, if converted into standard notation, we obtain a location of north,
west, which is about 40 miles NNW of Spokane. (Images made by https://www.gps-coordinates.net/). Note on the conversion into decimal:
and

It’s a shame that the designer of the postcard made this error, as I genuinely thought this was a clever and aesthetically pleasing design idea for a postcard.
While I’m not sure how this mistake happened, my best guess is that the designer used the location of north,
west — which is indeed in Spokane — and then misconverted from decimal notation to minutes and seconds.


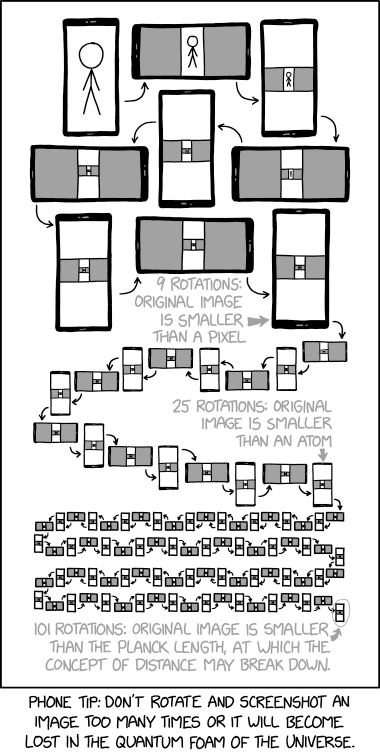
Source: https://xkcd.com/2671/

Source: https://xkcd.com/2687/
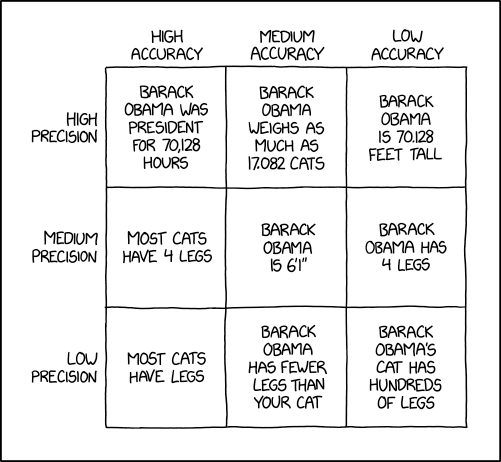
Source: https://xkcd.com/2696/
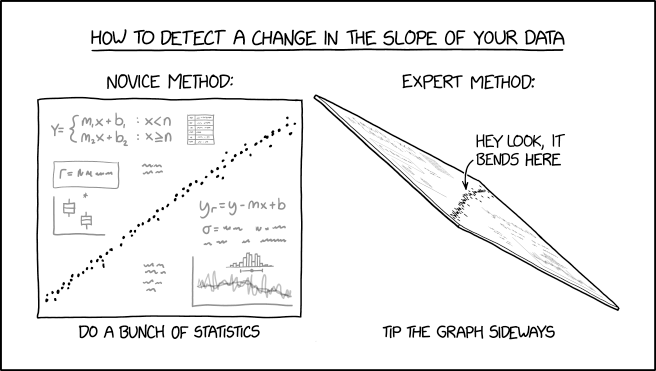
Source: https://xkcd.com/2701/

Source: https://xkcd.com/2711/
