What is your go-to dance move?

This is frivolous but fun, and it made me smile. Well done.

View this post on Instagram

A post shared by DaleDuo (@dale.duo)

Engaging students: Deriving the double angle formulas for sine, cosine, and tangent

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place. I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course). This student submission comes from my former student Morgan Mayfield. His topic, from Precalculus: deriving the double angle formulas for sine, cosine, and tangent.

How could you as a teacher create an activity or project that involves your topic? I want to provide some variety for opportunities to make this an engaging opportunity for Precalculus students and some Calculus students. Here are my three thoughts: IDEA 1: For precalculus students in a regular or advanced class, have them derive this formula in groups. After students are familiar with the Pythagorean identities and with angle sum identities, group students and ask them to derive a formula for double angles Sin(2θ), Cos(2θ), Tan(2θ). Let them struggle a bit, and if needed give them some hints such as useful formulas and ways to represent multiplication so that it looks like other operations. From here, encourage students to simplify when they can and challenge students to find the other formulas of Cos(2θ). Ask students to speculate instances when each formula for Cos(2θ) would be advantageous. This gives students confidence in their own abilities and show how math is interconnected and not just a bunch of trivial formulas. Lastly, to challenge students, have them come up with an alternative way to prove Tan(2θ), notably Sin(2θ)/Cos(2θ). This would make an appropriate activity for students while having them continue practicing proving trigonometric identities. IDEA 2: This next idea should be implemented for an advanced Precal class, and only when there is some time to spare. Euler was an intelligent man and left us with the Euler’s Formula: $e^{ix}=\cos x + i \sin x$ . Have Precalculus students suspend their questions about where it comes from and what it is used for. This is not something they would use in their class. Reassure them that for what they will do, all they need to understand is imaginary numbers, multiplying imaginary numbers, and laws of exponents. Have them plug in x = A + B and simplify the right-hand side of the equation so that we get: $\cos(A+B)+i\sin(A+B)= a + bi$ where $a$ and $b$ are two real numbers. The goal here is to get $\cos(A+B)+i\sin(A+B)= \cos \theta \cos \theta - \sin \theta \sin \theta + (\sin \theta \cos \theta + \cos \theta \sin \theta)i$ . All the steps to get to this point is Algebra, nothing out of their grasp. Now, the next part is to really get their brains going about what meaning we can make of this. If they are struggling, have them think about the implications of two imaginary numbers being equal; the coefficient of the real parts and imaginary parts must be equal to each other. Lastly, ask them if these equations seem familiar, where are they from, and what are they called…the angle sum formulas. From here, this can lead into what if x=2A? Students will either brute force the formula again, and others will realize x = A + A and plug it in to the equation they just derived and simplify. This idea is a 2-in-1 steal for the angle sum formulas and double angle formulas. It’s biggest downside is this is for Sin(2θ) and Cos(2θ). IDEA 3: Take IDEA 2, and put it in a Calculus 2 class. Everything that the precalculus class remains, but now have the paired students prove the Euler’s Formula using Taylor Series. Guide them through using the Taylor Series to figure out a Taylor Series representation of $e^x$ , $sin x$ , and $cos x$ . Then ask students to find an expanded Taylor Series of to 12 terms with ellipses, no need to evaluate each term, just the precise term. Give hints such as $i^2= -1$ and to consider $i^3=i^2 \cdot i = -i$ and other similar cases. Lastly, ask students to separate the extended series in a way that mimics $a + bi$ using ellipses to shows the series goes to infinity. What they should find is something like this:

Look familiar? Well it is the addition of two Taylor Series that represent Sin(x) and Cos(x). This is the last connection students need to make. Give hints to look through their notes to see why the “a” and “b” in the imaginary number look so familiar. This, is just one way to prove Euler’s Formula, then you can continue with IDEA 2 until your students prove the angle sum formulas and double angle formulas.

How does this topic extend what your students should have learned in previous courses? Students in Texas will typically be exposed to the Pythagorean Theorem in 8^th grade. At this stage, students use $a^2+b^2=c^2$ to find a missing side length. Students may also be exposed to Pythagorean triples at this stage. Then at the Geometry level or in a Trigonometry section, students will be exposed to the Pythagorean Identity. The Identity is $\sin^2 \theta + \cos^2 \theta = 1$ . I think that this is not fair for students to just learn this identity without connecting it to the Pythagorean Theorem. I think it would be a nice challenge student to solve for this identity by using a right triangle with hypotenuse c so that Sin (θ) = b/c and cos (θ) = a/c, one could then show either $c^2 \sin^2 \theta + c^2 \cos^2 \theta = c^2$ and thus $c^2(\sin^2 \theta + \cos^2 \theta) = c^2$ or one could show $(a/c)^2 + (b/c)^2 = (c/c)^2 = 1$ (using the Pythagorean theorem). From here, students learn about the angle addition and subtraction formulas in Precalculus. This is all that they need to derive the double angle formulas.

$\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$

$\sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta$

$\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$

$\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$

$\tan(\alpha + \beta) = \displaystyle \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}$

$\tan(\alpha - \beta) = \displaystyle \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta}$

This would be a good challenge exercise for students to do in pairs. Sin(2θ) = Sin(θ + θ), Cos(2 θ) = Cos(θ + θ), Tan(2θ) = Tan(θ + θ). Now we can apply the angle sum formula where both angles are equal: Sin(2θ) = sin(θ)cos(θ) + cos(θ)sin(θ) = 2sin(θ)cos(θ) Cos(2θ) = cos(θ)cos(θ) – sin(θ)sin(θ) = (We use a Pythagorean Identity here) Tan(2θ) = $\displaystyle \frac{\tan \theta + \tan \theta}{1 - \tan^2 \theta} = \frac{2 \tan \theta}{1-\tan^2 \theta}$ Bonus challenge, use Sin(2θ) and Cos(2θ) to get Tan(2θ). Well, if $\tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta}$ , then

$\tan 2\theta = \displaystyle \frac{\sin 2\theta}{\cos 2\theta}$

$= \displaystyle \frac{2 \sin \theta \cos \theta}{\cos^2 \theta - \sin^2 \theta}$

$= \displaystyle \frac{ \frac{2 \sin \theta \cos \theta}{\cos^2 \theta} }{ \frac{\cos^2 \theta - \sin^2 \theta}{\cos^2 \theta} }$

$= \displaystyle \frac{2 \tan \theta}{1 - \tan^2 \theta}$

The derivations are straight forward, and I believe that many students get off the hook by not being exposed to deriving many trigonometric identities and taking them as facts. This is in the grasp of an average 10^th to 12^th grader.

What are the contributions of various cultures to this topic? I have included four links that talk about the history of Trigonometry. It seemed that ancient societies would need to know about the Pythagorean Identities and the angles sum formulas to know the double angle formulas. Here is our problem, it’s hard to know who “did it first?” and when “did they know it?”. Mathematical proofs and history were not kept as neatly written record but as oral traditions, entertainment, hobbies, and professions. The truth is that from my reading, many cultures understood the double angle formula to some extent independently of each other, even if there was no formal proof or record of it. Looking back at my answer to B2, it seems that the double angle formula is almost like a corollary to knowing the angle sum formulas, and thus to understand one could imply knowledge of the other. Perhaps, it was just not deemed important to put the double angle formula into a category of its own. Many of the people who figured out these identities were doing it because they were astronomers, navigators, or carpenters (construction). Triangles and circles are very important to these professions. Knowledge of the angle sum formula was known in Ancient China, Ancient India, Egypt, Greece (originally in the form of broken chords theorem by Archimedes), and the wider “Medieval Islamic World”. Do note that that Egypt, Greece, and the Medieval Islamic World were heavily intertwined as being on the east side of the Mediterranean and being important centers of knowledge (i.e. Library of Alexandria.) Here is the thing, their knowledge was not always demonstrated in the same way as we know it today. Some cultures did have functions similar to the modern trigonometric functions today, and an Indian mathematician, Mādhava of Sangamagrāma, figured out the Taylor Series approximations of those functions in the 1400’s. Greece and China for example relayed heavily on displaying knowledge of trigonometry in ideas of the length of lines (rods) as manifestations of variables and numbers. Ancient peoples didn’t have calculators, and they may have defined trigonometric functions in a way that would be correct such as the “law of sines” or a “Taylor series”, but still relied on physical “sine tables” to find a numerical representation of sine to n numbers after the decimal point. How we think of Geometry and Trigonometry today may have come from Descartes’ invention of the Cartesian plane as a convenient way to bridge Algebra and Geometry. References: https://www.mathpages.com/home/kmath205/kmath205.htm https://en.wikipedia.org/wiki/History_of_trigonometry https://www.ima.umn.edu/press-room/mumford-and-pythagoras-theorem

Engaging students: Defining sine, cosine and tangent in a right triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Jessica Williams. Her topic, from Precalculus: defining sine, cosine and tangent in a right triangle.

How could you as a teacher create an activity or project that involves your topic?

I know of a good project/activity for the students to do that will be extremely engaging. You could either do this for an elaborate activity for your students or maybe an opening activity for day 2 of a lesson. For my class, I would get a square cookie cake, and have the slices cut into right triangles. I would allow each student to have a piece (but not eat it just yet). The students will be provided with rulers and a protractor. The students will each measure the hypotenuse of their cookie cake and the degree of whichever angle you would like them to measure, however each student should be measuring the same parts so do this unanimously). As a class, decide on an average for the measurements for everyone to use so that the data is not off. Then take the supplies away from the students and ask the students to find the rest of the missing sides and angles of their piece of cookie cake. They will also be provided with a worksheet to go along with this activity. This is a good review activity or al elaborate activity to allow further practice of real world application of right triangle trigonometry. Then go over as a class step by step how they solved for their missing angles and side lengths and make each group be accountable for sharing one of them. This allows the students to all be actively participating. Through out the lesson, make sure to tell the kids as long as they are all participating they will get to eat their slice when the lesson is done. Lastly, allow the students to eat their slice of cookie cake.

How does this topic extend what your students should have learned in previous courses?

Prior to learning about right triangle trigonometry the students will know how to use the Phythagorean Theorem to find how long the missing side length is of a right triangle. The students know basic triangle information such as, the sum of the angles in a triangle is 180 degrees. The students already know the difference between the hypotenuse and the other two legs. The students know that hypotenuse will be the longest leg and the leg across from the 90 degree angle. The students will also know the meaning of a fraction or ratio. The students may need some refreshing of memory on some parts of prior knowledge, but as teachers we know this is an extremely important part of a lesson plan. Even as teacher we tend to forget things and require a jog of memory. A simple activity such as headbands or a kahoot with vocabulary would be an excellent idea for accessing the students prior knowledge. This allows the students to formally assess themselves and where they stand with the knowledge. Also, it allows the teacher to formally assess the students and see what they remember or parts they are struggling on. This allows the teacher to know what things to spend more time on.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

Technology is always an amazing aspect of the classroom. Like stated above, a vocab review using headbands or kahoot would be a good idea for this type of lesson that DEFINITELY needs prior knowledge to be applied in order to succeed. Also, showing the students how to plug in sine, cosine, and tangent is crucial. They have seen these buttons on the calculator but they do not know what they mean or how to use them. Using an online TI on display for the class is great. I had to do this with my 10th grade students to make sure they understood how to use the 3 buttons. Also, when using arcsin, arccos, and arctan it can be confusing. Using technology to show the class as a whole is the best route to go. Also, technology can used as review for a homework assignment or even extra credit for the students. It benefits them by getting extra review and extra credit points. I found a website called http://www.learnalberta.ca/content/mejhm/index.html?l=0&ID1=AB.MATH.JR.SHAP&ID2=AB.MATH.JR.SHAP.TRI&lesson=html/object_interactives/trigonometry/use_it.html , which is a golf game that requires review of triangles and trigonometry. It allows the students to practice the ratios of SOH-CAH-TOA using a given triangle.

Engaging students: Defining sine, cosine and tangent in a right triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Jessica Williams. Her topic, from Geometry: defining sine, cosine and tangent in a right triangle.

How could you as a teacher create an activity or project that involves your topic?

I’ve actually had the opportunity to teach this lesson to my 10th graders last semester. It is a difficult concept for the students to understand, however if you teach it in a way the students are actively engaged, it helps extremely. Prior to this lesson, the students knew about the hypotenuse and knew the other sides lengths as “legs.” We started by calling 3 students up to the front to hold up our three triangle posters. (triangle cut outs with the 90 degree angle showing and then there was an agle missing). We asked the students how we could find a missing angle given only one side length. For starters, I demonstrated on one triangle by placing a spray water bottle at the missing angle given, and spray the water across.
I will then ask one student to come up to help me demonstrate on the other two triangles. We asked the student where the water is spraying. All of them said words along the lines of “across, away from the angle.” We eventually got to the word opposite. Then we called two students up to demonstrate with the water bottle to determine which side is opposite. If we always know the hypotenuse is the leg across from 90 degree angle, and the opposite side is the one across from the missing angle, then we discovered the last leg must be the adjacent side. Which adjacent means, “next to” or “beside”. Next, we teacher-lead the students through a SOH-CAH-TOA foldable under the doc cam. This was important because they used to later to answer multiple questions using smart pals. Smart pal questions on the board, allowed for EACH student to have to answer and show their work on their smart pal in order to hold it up once we asked for answers. This allowed for formative assessment for the teachers and for the students to see if they were correctly answering the questions. Next we incorporated a “find someone who” Kagan structure tool, which allowed the students to all be actively engaged and answering questions regarding the task. Then we explained and went over misconceptions as a class. It was a very successful lesson overall, and the students were all actively engaged the entire time!

What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?

Trigonometry was originally developed for the use of sailing as a navigation method. The origins can be traced back to ancient Egypt, the Indus Valley, and Mesopotamia. This was over 4000 years ago. Measuring angles in degrees, minutes, and seconds comes from the Babylonian’s base 60 system of numbers. In 150 B.C.E, Hipparchus made a trigonometric table using sine to solve triangles. Later on, Ptolemy extended the trig calculations in 100 C.E. Also, in interesting fact is the ancient Sinhalese used trig to calculate for water flow. Persian mathematician Abul Wafa introduced the angle addition identities. As you can see, there are MANY different mathematicians who distributed to the topic of trigonometry. A lot of them built upon previous work and discovered new formulas, identities, etc. It’s amazing to see how even trigonometry is used to every day life. You always hear people say, “When will I ever use this is life?” and it bugs me to hear this. However, I always have examples of how math is used in our everyday world and from a past long ago that advanced us to where we are today.

How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?

I would show this video that I found on youtube. I would exclude the first movie example that involves shooting, however the rest are great examples.

Showing movie clips to students is always a great way to grab their attention. Visually showing them that math is a part of movies, and every day life shows them that it is important. This video would also be great to use as practice problem, but blur out one of the side lengths or angles missing. You could play the movie scene then pause it on the part with the triangle and have the students solve for missing angle or side length. It would be a fun activity for the students and involve great practice. You could even make this a homework assignment. It’s engaging to watch and keeps the student’s attention while doing homework. The video shows that math is involved in dancing, buildings, etc. This activity also can excite students to try to find math in the movies or tv shows that the watch. You could assign the students to pay attention to to the next couple of shows or movies the watch and to bring back to class an example or two of how math was incorporated in it. Mathematics goes unnoticed because it is honestly part of our everyday norm/lifestyle.

References: https://www.youtube.com/watch?v=LYNN0OYDUB4

http://www.newworldencyclopedia.org/entry/Trigonometry

I Have a Tan

Source: https://www.facebook.com/WowSoPunny/photos/a.985057168177019.1073741829.984774068205329/1634769573205772/?type=3&theater

Trigonometry pun

Source: https://www.facebook.com/743378802479548/photos/a.743768985773863.1073741828.743378802479548/792810117536416/?type=3&theater

Engaging students: Deriving the double angle formulas for sine, cosine, and tangent

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Daniel Adkins. His topic, from Precalculus: deriving the double angle formulas for sine, cosine, and tangent.

How does this topic extend what your students should have already learned?

A major factor that simplifies deriving the double angle formulas is recalling the trigonometric identities that help students “skip steps.” This is true especially for the Sum formulas, so a brief review of these formulas in any fashion would help students possibly derive the equations on their own in some cases. Listed below are the formulas that can lead directly to the double angle formulas.

A list of the formulas that students can benefit from recalling:

Sum Formulas:
- sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
- cos(a+b) = cos(a)cos(b) – sin(a)sin(b)
- tan(a+b) = [tan(a) +tan(b)] / [1-tan(a)tan(b)]

Pythagorean Identity:
- Sin² (a) + Cos²(a) = 1

This leads to the next topic, an activity for students to attempt the equation on their own.

How could you as a teacher create an activity or project that involves your topic?

I’m a firm believer that the more often a student can learn something of their own accord, the better off they are. Providing the skeletal structure of the proofs for the double angle formulas of sine, cosine, and tangent might be enough to help students reach the formulas themselves. The major benefit of this is that, even though these are simple proofs, they have a lot of variance on how they may be presented to students and how “hands on” the activity can be.

I have an example worksheet demonstrating this with the first two double angle formulas attached below. This is in extremely hands on format that can be given to students with the formulas needed in the top right corner and the general position where these should be inserted. If needed the instructor could take this a step further and have the different Pythagorean Identities already listed out (I.e. Cos²(a) = 1 – Sin²(a), Sin²(a) = 1 – Cos²(a)) to emphasize that different formats could be needed. This is an extreme that wouldn’t take students any time to reach the conclusions desired. Of course a lot of this information could be dropped to increase the effort needed to reach the conclusion.

A major benefit with this also is that even though they’re simple, students will still feel extremely rewarded from succeeding on this paper on their own, and thus would be more intrinsically motivated towards learning trig identities.

How can Technology be used to effectively engage students with this topic?

When it comes to technology in the classroom, I tend to lean more on the careful side. I know me as a person/instructor, and I know I can get carried away and make a mess of things because there was so much excitement over a new toy to play with. I also know that the technology can often detract from the actual math itself, but when it comes to trigonometry, and basically any form of geometric mathematics, it’s absolutely necessary to have a visual aid, and this is where technology excels.

The Wolfram Company has provided hundreds of widgets for this exact purpose, and below, you’ll find one attached that demonstrates that sin(2a) appears to be equal to its identity 2cos(a)sin(a). This is clearly not a rigorous proof, but it will help students visualize how these formulas interact with each other and how they may be similar. The fact that it isn’t rigorous may even convince students to try to debunk it. If you can make a student just irritated enough that they spend a few minutes trying to find a way to show you that you’re wrong, then you’ve done your job in that you’ve convinced them to try mathematics for a purpose.

After all, at the end of the day, it doesn’t matter how you begin your classroom, or how you engage your students, what matters is that they are engaged, and are willing to learn.

Wolfram does have a free cdf reader for its demonstrations on this website: http://demonstrations.wolfram.com/AVisualProofOfTheDoubleAngleFormulaForSine/

References

My Favorite One-Liners: Part 106

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

Years ago, when I first taught Precalculus at the college level, I was starting a section on trigonometry by reminding my students of the acronym SOHCAHTOA for keeping the trig functions straight:

$\sin \theta = \displaystyle \frac{\hbox{Opposite}}{\hbox{Hypotenuse}}$ ,

$\cos \theta = \displaystyle \frac{\hbox{Adjacent}}{\hbox{Hypotenuse}}$ ,

$\tan \theta = \displaystyle \frac{\hbox{Opposite}}{\hbox{Adjacent}}$ .

At this point, one of my students volunteered that a previous math teacher had taught her an acrostic to keep these straight: Some Old Hippie Caught Another Hippie Tripping On Acid.

Needless to say, I’ve been passing this pearl of wisdom on to my students ever since.

My Favorite One-Liners: Part 69

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

This story, that I’ll share with my Precalculus students, comes from Fall 1996, my first semester as a college professor. I was teaching a Precalculus class, and the topic was vectors. I forget the exact problem (believe me, I wish I could remember it), but I was going over the solution of a problem that required finding $\tan^{-1}(7)$ . I told the class that I had worked this out ahead of time, and that the approximate answer was $82^o$ . Then I used that angle for whatever I needed it for and continued until obtaining the eventual solution.

(By the way, I now realize that I was hardly following best practices by computing that angle ahead of time. Knowing what I know now, I should have brought a calculator to class and computed it on the spot. But, as a young professor, I was primarily concerned with getting the answer right, and I was petrified of making a mistake that my students could repeat.)

After solving the problem, I paused to ask for questions. One student asked a good question, and then another.

Then a third student asked, “How did you know that $\tan^{-1}(7)$ was $82^o$ ?

Suppressing a smile, I answered, “Easy; I had that one memorized.”

The class immediately erupted… some with laughter, some with disbelief. (I had a terrific rapport with those students that semester; part of the daily atmosphere was the give-and-take with any number of exuberant students.) One guy in the front row immediately challenged me: “Oh yeah? Then what’s $\tan^{-1}(9)$ ?

I started to stammer, “Uh, um…”

“Aha!” they said. “He’s faking it.” They start pulling out their calculators.

Then I thought as fast as I could. Then I realized that I knew that $\tan 82^o \approx 7$ , thanks to my calculation prior to class. I also knew that $\displaystyle \lim_{x \to 90^-} \tan x = \infty$ since the graph of $y = \tan x$ has a vertical asymptote at $x = \pi/2 = 90^o$ . So the solution to $\tan x = 9$ had to be somewhere between $82^o$ and $90^o$ .

So I took a total guess. “ $84^o$ ,” I said, faking complete and utter confidence.

Wouldn’t you know it, I was right. (The answer is about $83.66^o$ .)

In stunned disbelief, the guy who asked the question asked, “How did you do that?”

I was reeling in shock that I guessed correctly. But I put on my best poker face and answered, “I told you, I had it memorized.” And then I continued with the next example. For the rest of the semester, my students really thought I had it memorized.

To this day, this is my favorite stunt that I ever pulled off in front of my students.

Engaging students: Defining sine, cosine and tangent in a right triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Loc Nguyen. His topic, from Geometry: defining sine, cosine and tangent in a right triangle.

What interesting (i.e., uncontrived) word problems using this topic can your students do now?

There are many real world applications that involve in this topic and I will incorporate some problems in real life to engage the students. Suppose I have a classroom that has the shape of rectangular prism. I will begin my lesson by challenging the students to find the height of the classroom and of course I will award them with something cool. I believe this will ignite students’ curiosity and excitement to participate into the problem. In the process of finding the height, I will gradually introduce the concept of right triangle trigonometry. The students will learn the relationship of ratios of the sides in the triangle. Eventually, the students will realize that they need this concept for finding the height of the classroom. I will pose some guiding questions to drive them toward the solution. Such questions could be: what can I measure? Can we measure the angle from our eyes to the opposite corner of the ceiling point? What formula will help me to find the height?

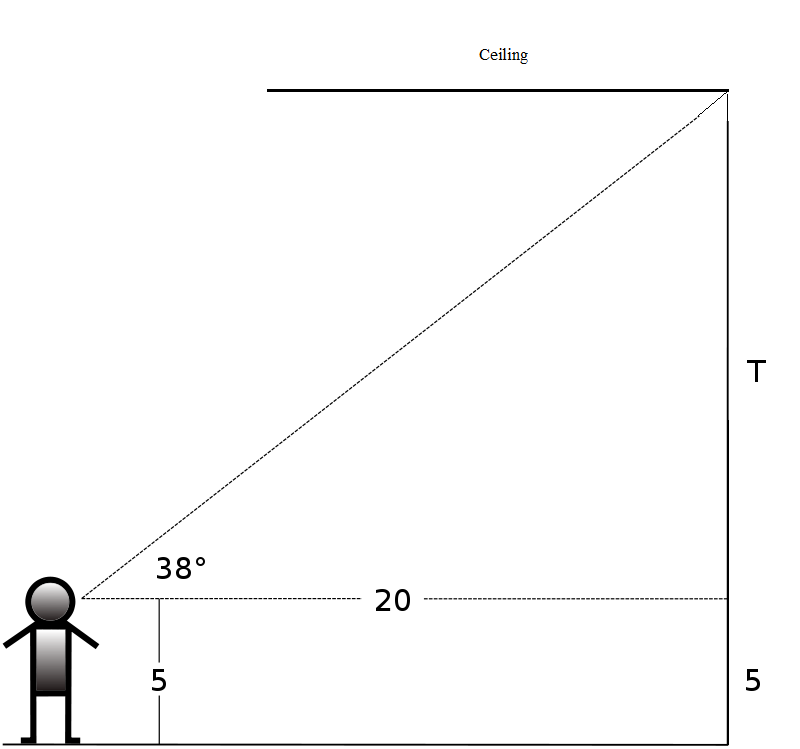
After this problem I will provide them many different real world problems to practice such as:

How can this topic be used in your students’ future courses in mathematics or science?

Knowing how to compute sine, cosine or tangent in the right triangle will help students a lot when they get to higher level math or other science class, especially Physics. In higher level math, students will always have the chance to encounter this concept. For example, in Pre-Calculus, the students will likely learn about polar system. This requires students to have the strong fundamental understandings of sine, cosine and tangent in a right triangle. Students will be asked to convert from the Cartesian system to polar system, or vice versa. If they do not grasp the ideas of this topic, they will eventually encounter huge obstacles in future. In science, especially physics, the students will learn a lot about the motions of an objects. This will involve concepts of force, velocity, speed, momentum. The students will need to understand the how to compute sine, cosine and tangent in the right triangle so that they can easily know how to approach the problems in physics.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

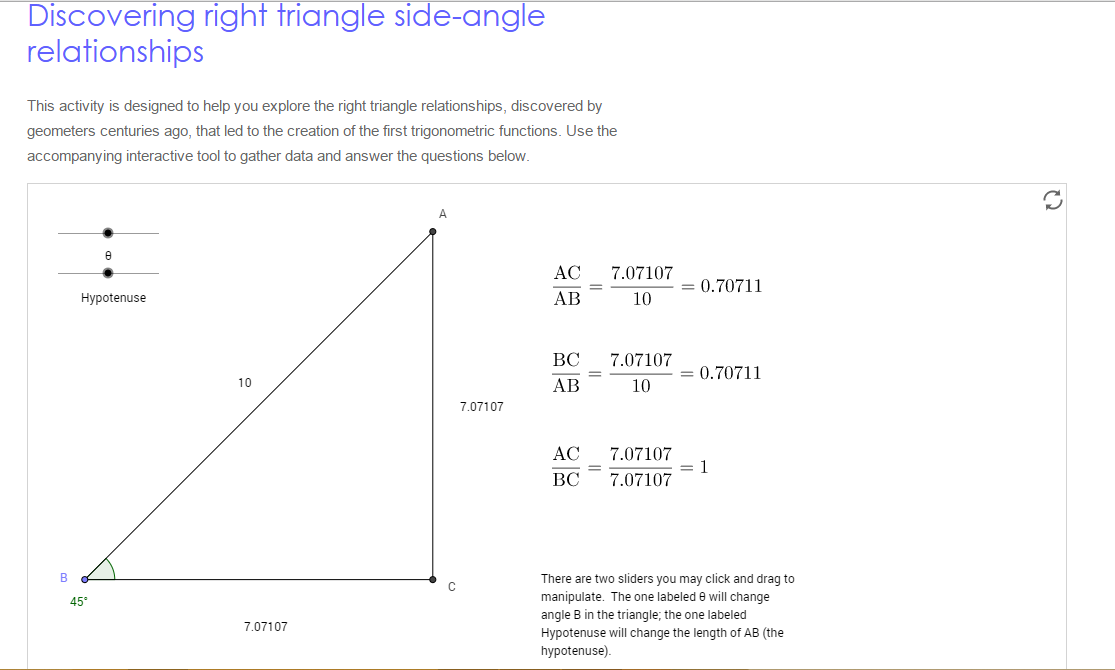
This website, https://www.geogebra.org/material/simple/id/48148 , can be a great tool for the students to understand the relationships of the sides in the right triangle. The website creates an activity for students to explore the ratios of the sides such as AC/BC, AC/AB, and BC/AB. The students will observe the changes of the ratios based on the changes of theta and side BC which is the hypotenuse. At this point, the students will be introduced the name of each side of the right triangle which corresponds to theta such as opposite, adjacent and hypotenuse. This activity allows the students to visualize what happens to the triangle when we change the angle or its side lengths. The students will then explore the activity to find interesting facts about the side ratios. I will pose some questions to help the students understand the relationships of side ratios. Such questions could be: What type of triangle is it? Tell me how the triangle changes as we change the hypotenuse or angle. If we know one side length and the angle, how can we find the other side lengths? Those questions allow me to introduce the terms sine, cosine, and tangent in the right triangle.

References

https://en.wikibooks.org/wiki/High_School_Trigonometry/Applications_of_Right_Triangle_Trigonometry

https://www.geogebra.org/material/simple/id/48148