Inverse Functions: nth Roots (Part 7)

In the previous posts of this series, I carefully considered the definition of $f(x) = \sqrt{x} = x^{1/2}$ . Let’s now repeat this logic to consider the definition of $f(x) = \sqrt[n]{x} = x^{1/n}$ , where $n \ge 3$ is an integer. We begin with $n$ even.

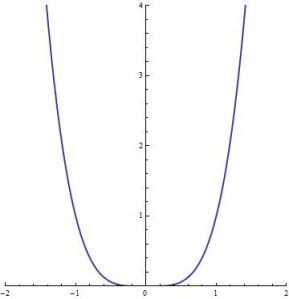
A typical case is $n =4$ ; the graph of $y = x^4$ is shown below.

The full graph of $y= x^n$ fails the horizontal line test if $n$ is even. Therefore, we need to apply the same logic that we used earlier to define $y = \sqrt[n]{x}$ . In particular, we essentially erase the left half of the graph. By restricting the domain to $[0,\infty)$ , we create a new function that does satisfy the horizontal line test, so that the graph of $y = \sqrt[n]{x}$ is found by reflecting through the line $y = x$ .

Written in sentence form,

If $n$ is even, then $y = \sqrt[n]{x}$ means that $x = y^n$ and $y \ge 0$ . In particular, this is impossible for real $y$ if $x < 0$ .

green line
We now turn to the case of $n$ odd. Unlike before, the full graph of $y= x^n$ (in thick blue) satisfies the horizontal line test. Therefore, there is no need to restrict the domain to define the inverse function. (shown in thin purple).

In other words,

If $n$ is odd, then $y = \sqrt[n]{x}$ means that $x = y^n$ . There is no need to give a caveat on the possible values of $y$ .

In particular, $\sqrt{-8}$ and $\sqrt[4]{-8}$ are both undefined since there is no (real) number $x$ so that $x^2 = -8$ or $x^4 = -8$ . However, $\sqrt[3]{-8}$ is defined and is equal to $-2$ since $(-2)^3 = -8$ .