Difference of Two Powers (Index)

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on getting students to discover the formula for factoring $x^n - y^n$ .

Part 1: A numerical way of discovering the formula for $x^2 - y^2$ .

Part 2: A geometric way of discovering the formula for $x^2 - y^2$ .

Part 3: Pedagogical thoughts on the importance of students discovering the formula for $x^3 - y^3$ .

Part 4: A geometric way of discovering the formula for $x^3 - y^3$ .

Part 5: Guiding students to the formula for $x^n - y^n$ .

Langley’s Adventitious Angles: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my short series on a couple of easily stated but remarkably difficult geometry problems.

Part 1: The world’s second hardest easy geometry problem.

Part 2: The world’s hardest easy geometry problem.

The Shortest Known Paper Published in a Serious Math Journal

Source: http://www.openculture.com/2015/04/shortest-known-paper-in-a-serious-math-journal.html

Euler’s conjecture, a theory proposed by Leonhard Euler in 1769, hung in there for 200 years. Then L.J. Lander and T.R. Parkin came along in 1966, and debunked the conjecture in two swift sentences. Their article — which is now open access and can be downloaded here — appeared in the Bulletin of the American Mathematical Society.

Predicate Logic and Popular Culture: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on using examples from popular culture to illustrate principles of predicate logic.

Unlike other series that I’ve made, this series didn’t have a natural chronological order. So I’ll list these by concept illustrated from popular logic.

Logical and $\land$ : Part 1

Part 1: “You Belong To Me,” by Taylor Swift
Part 21: “Do You Hear What I Hear,” covered by Whitney Houston
Part 31: The Godfather (1972)
Part 45: The Blues Brothers (1980)
Part 53: “What Does The Fox Say,” by Ylvis
Part 54: “Billie Jean,” by Michael Jackson

Logical or $\lor$ :

Part 1: Shawshank Redemption (1994)

Logical negation $\lnot$ :

Part 1: Richard Nixon
Part 32: “Satisfaction!”, by the Rolling Stones
Part 39: “We Are Never Ever Getting Back Together,” by Taylor Swift

Logical implication $\Rightarrow$ :

Part 1: Field of Dreams (1989), and also “Roam,” by the B-52s
Part 2: “Word Crimes,” by Weird Al Yankovic
Part 7: “I’ll Be There For You,” by The Rembrandts (Theme Song from Friends)
Part 43: “Kiss,” by Prince
Part 50: “I’m Still A Guy,” by Brad Paisley

For all $\forall$ :

Part 3: Casablanca (1942)
Part 4: A Streetcar Named Desire (1951)
Part 34: “California Girls,” by The Beach Boys
Part 37: Fellowship of the Ring, by J. R. R. Tolkien
Part 49: “Buy Me A Boat,” by Chris Janson
Part 57: “Let It Go,” by Idina Menzel and from Frozen (2013)

For all and implication:

Part 8 and Part 9: “What Makes You Beautiful,” by One Direction
Part 13: “Safety Dance,” by Men Without Hats
Part 16: The Fellowship of the Ring, by J. R. R. Tolkien
Part 24 : “The Chipmunk Song,” by The Chipmunks
Part 55: The Quiet Man (1952)

There exists $\exists$ :

Part 10: “Unanswered Prayers,” by Garth Brooks
Part 15: “Stand by Your Man,” by Tammy Wynette (also from The Blues Brothers)
Part 36: Hamlet, by William Shakespeare
Part 57: “Let It Go,” by Idina Menzel and from Frozen (2013)

Existence and uniqueness:

Part 14: “Girls Just Want To Have Fun,” by Cyndi Lauper
Part 20: “All I Want for Christmas Is You,” by Mariah Carey
Part 23: “All I Want for Christmas Is My Two Front Teeth,” covered by The Chipmunks
Part 29: “You’re The One That I Want,” from Grease
Part 30: “Only You,” by The Platters
Part 35: “Hound Dog,” by Elvis Presley

DeMorgan’s Laws:

Part 5: “Never Gonna Give You Up,” by Rick Astley
Part 28: “We’re Breaking Free,” from High School Musical (2006)

Simple nested predicates:

Part 6: “Everybody Loves Somebody Sometime,” by Dean Martin
Part 25: “Every Valley Shall Be Exalted,” from Handel’s Messiah
Part 33: “Heartache Tonight,” by The Eagles
Part 38: “Everybody Needs Somebody To Love,” by Wilson Pickett and covered in The Blues Brothers (1980)
Part 46: “Mean,” by Taylor Swift
Part 56: “Turn! Turn! Turn!” by The Byrds

Maximum or minimum of a function:

Part 12: “For the First Time in Forever,” by Kristen Bell and Idina Menzel and from Frozen (2013)
Part 19: “Tennessee Christmas,” by Amy Grant
Part 22: “The Most Wonderful Time of the Year,” by Andy Williams
Part 48: “I Got The Boy,” by Jana Kramer
Part 60: “I Loved Her First,” by Heartland

Somewhat complicated examples:

Part 11 : “Friends in Low Places,” by Garth Brooks
Part 27 : “There is a Castle on a Cloud,” from Les Miserables
Part 41: Winston Churchill
Part 44: Casablanca (1942)
Part 51: “Everybody Wants to Rule the World,” by Tears For Fears
Part 58: “Fifteen,” by Taylor Swift
Part 59: “We Are Never Ever Getting Back Together,” by Taylor Swift
Part 61: “Style,” by Taylor Swift

Fairly complicated examples:

Part 17 : Richard Nixon
Part 47: “Homegrown,” by Zac Brown Band
Part 52: “If Ever You’re In My Arms Again,” by Peabo Bryson

Really complicated examples:

Part 18: “Sleigh Ride,” covered by Pentatonix
Part 26: “All the Gold in California,” by the Gatlin Brothers
Part 40: “One of These Things Is Not Like the Others,” from Sesame Street
Part 42: “Take It Easy,” by The Eagles

The antiderivative of 1/(x^4+1): Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on the computation of

$\displaystyle \int \frac{dx}{x^4+1}$

Part 1: Introduction.

Part 2: Factoring the denominator using De Moivre’s Theorem.

Part 3: Factoring the denominator using the difference of two squares.

Part 4: The partial fractions decomposition of the integrand.

Part 5: Partial evaluation of the resulting integrals.

Part 6: Evaluation of the remaining integrals.

Part 7: An apparent simplification using a trigonometric identity.

Part 8: Discussion of the angles for which the identity holds.

Part 9: Proof of the angles for which the identity holds.

Part 10: Implications for using this identity when computing definite integrals.

Different Ways of Solving a Contest Problem: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on different ways of solving the contest problem “If $3 \sin \theta = \cos \theta$ , what is $\sin \theta \cos \theta$ ?”

Part 1: Drawing the angle $\theta$

Part 2: A first attempt using a Pythagorean identity.

Part 3: A second attempt using a Pythagorean identity and the original hypothesis for $\theta$ .

Is 2i less than 3i? (Index)

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on why it doesn’t make sense to say one complex number is less than another complex number (using the usual definition of “less than”).

Part 1: A sketch of a direct proof based on the order axioms proving that $i$ is not an element of a number system that has the usual definition of inequality.

Part 2: An indirect proof.

Part 3: Discussion about the lexicographic ordering, which almost works.

Part 4: Two other partial orderings which almost work.

Thoughts on Infinity (Part 3a)

Last summer, Math With Bad Drawings had a nice series on the notion of infinity that I recommend highly. This topic is a perennial struggle for math majors to grasp, and I like the approach that the author uses to sell this difficult notion.

Part 3 on infinite series and products that are conditionally convergent discusses a head-scratching fact: according to the Riemann series theorem, the commutative and associative laws do not apply to conditionally convergent series.

An infinite series $\displaystyle \sum_{n=1}^\infty a_n$ converges conditionally if it converges to a finite number but $\displaystyle \sum_{n=1}^\infty |a_n|$ diverges. Indeed, by suitably rearranging the terms, the sum can be changed so that the (rearranged) series converges to any finite value. Even worse, the terms can be rearranged so that the sum converges to either $\infty$ or $-\infty$ . (Of course, this can’t happen for finite sums, and rearrangements of an absolutely convergent series do not change the value of the sum.)

I really like Math With Bad Drawing’s treatment of the subject, as it starts with an infinite product for $\pi/2$ :

The top line is correct. However, the bottom line has to be incorrect since $\pi/2 > 1$ but each factor on the right-hand side is less than 1. The error, of course, stems from conditional convergence (the terms in the top product cannot be rearranged).

Conditional convergence is typically taught but glossed over in Calculus II since these rearrangements are such a head-scratching topic. I really like the above example because the flaw in the logic is made evidence after only three steps.

In tomorrow’s post, I’ll continue with another example of rearranging the terms in a conditionally convergent series.

Thoughts on Infinity (Part 2b)

Here’s Part 2 on the harmonic series, which is extremely well-written and which I recommend highly. Here’s a brief summary: the infinite harmonic series

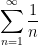
$\displaystyle \sum_{n=1}^\infty \frac{1}{n}$

diverges. However, if you eliminate from the harmonic series all of the fractions whose denominator contains a 9, then the new series converges! This series has been called the Kempner series, named after the mathematician who first published this result about 100 years ago.

Source: http://smbc-comics.com/index.php?id=3777

To prove this, we’ll examine the series whose denominators are between 1 and 8, between 10 and 88, between 100 and 888, etc. First, each of the terms in the partial sum

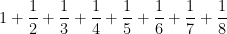
$\displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}$

is less than or equal to $1$ , and so the sum of the above eight terms must be less than $8$ .

Next, each of the terms in the sum

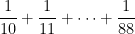
$\displaystyle \frac{1}{10} + \frac{1}{11} + \dots + \frac{1}{88}$

is less than 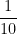$\displaystyle \frac{1}{10}$ . Notice that there are 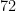$72$ terms in this sum since there are 8 possibilities for the first digit of the denominator (1 through 8) and 9 possibilities for the second digit (0 through 8). So the sum of these 72 terms must be less than $\displaystyle 8 \times \frac{9}{10}$ .

Next, each of the terms in the sum

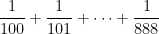
$\displaystyle \frac{1}{100} + \frac{1}{101} + \dots + \frac{1}{888}$

is less than $\displaystyle \frac{1}{100}$ . Notice that there are $8 \times 9 \times 9$ terms in this sum since there are 8 possibilities for the first digit of the denominator (1 through 8) and 9 possibilities for the second and third digits (0 through 8). So the sum of these $8 \times 9 \times 9$ terms must be less than $8 \times \displaystyle \frac{9^2}{100}$ .

Continuing, we see that the Kempner series is bounded above by

$\displaystyle 8 + 8 \times \frac{9}{10} + 8 \times \frac{9^2}{10^2} + \dots$

Using the formula for an infinite geometric series, we see that the Kempner series converges, and the sum of the Kempner series must be less than $8 \times \displaystyle \frac{1}{1-9/10} = 80$ .

Using the same type of reasoning, much sharper bounds for the sum of the Kempner series can also be found. This 100-year-old article from the American Mathematical Monthly demonstrates that the sum of the Kempner series is between $22.4$ and $23.3$ . For more information about approximating the sum of the Kempner series, see Mathworld and Wikipedia.

It should be noted that there’s nothing particularly special about the number $9$ in the above discussion. If all denominators containing $314159265$ , or any finite pattern, are eliminated from the harmonic series, then the resulting series will always converge.

Thoughts on Infinity (Part 2a)

Here’s Part 2 on the harmonic series, which is extremely well-written and which I recommend highly. Here’s a brief summary: the infinite harmonic series

$\displaystyle \sum_{n=1}^\infty \frac{1}{n}$

diverges. This is a perennial head-scratcher for students, as the terms become smaller and smaller yet the infinite series diverges.

To show this, notice that

$\displaystyle \frac{1}{3} + \frac{1}{4} > \displaystyle \frac{1}{4} + \frac{1}{4} = \displaystyle \frac{1}{2}$ ,

$\displaystyle \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} > \displaystyle \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \displaystyle \frac{1}{2}$ ,

and so on. Therefore,

$\displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} > \displaystyle 1 + \frac{1}{2} + \frac{1}{2} = 2$ ,

$\displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} +\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} > \displaystyle 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \displaystyle \frac{5}{2}$ ,

and, in general,

$\displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{2^n} > \displaystyle 1+\frac{n}{2}$ .

Since $\displaystyle \lim_{n \to \infty} \left(1 + \frac{n}{2} \right) = \infty$ , we can conclude that the harmonic series diverges.

However, here’s an amazing fact which I hadn’t known before the Math With Bad Drawings post: if you eliminate from the harmonic series all of the fractions whose denominator contains a 9, then the new series converges!

I’ll discuss the proof of this fact in tomorrow’s post. Until then, here’s a copy of the comic used in the Math With Bad Drawings post.

Source: http://smbc-comics.com/index.php?id=3777