Why do we still require students to rationalize denominators?

Which answer is simplified: $\displaystyle \frac{1}{2 \sqrt{2}}$ or $\displaystyle \frac{ \sqrt{2} }{4}$ ? From example, here’s a simple problem from trigonometry:

Suppose $\theta$ is an acute angle so that $\sin \theta = \displaystyle \frac{1}{3}$ . Find $\tan \theta$ .

To solve, we make a right triangle whose side opposite of $\theta$ has length $1$ and hypotenuse with length $3$ . The adjacent side has length $\sqrt{3^2 - 1^2} = \sqrt{8} = 2\sqrt{2}$ . Therefore,

$\tan \theta = \displaystyle \frac{ \hbox{Opposite} }{ \hbox{Adjacent} } = \displaystyle \frac{1}{2 \sqrt{2}}$

This is the correct answer, and it could be plugged into a calculator to obtain a decimal approximation. However, in my experience, it seems that most students are taught that this answer is not yet simplified, and that they must rationalize the denominator to get the “correct” answer:

$\tan \theta = \displaystyle \frac{1}{2 \sqrt{2}} \cdot \frac{ \sqrt{2} }{ \sqrt{2} } = \displaystyle \frac{ \sqrt{2} }{4}$

Of course, this is equivalent to the first answer. So my question is philosophical: why are students taught that the first answer isn’t simplified but the second is? Stated another way, why is a square root in the numerator so much more preferable than a square root in the denominator?

Feel free to correct me if I’m wrong, but it seems to me that rationalizing denominators is a vestige of an era before cheap pocket calculators. Let’s go back in time to an era before pocket calculators… say, 1927, when The Jazz Singer was just released and stars of silent films, like Don Lockwood, were trying to figure out how to act in a talking movie.

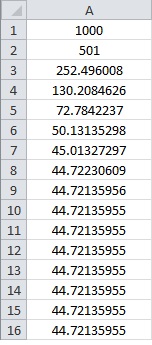
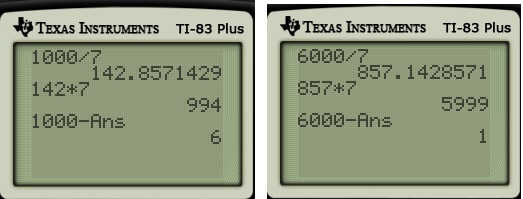
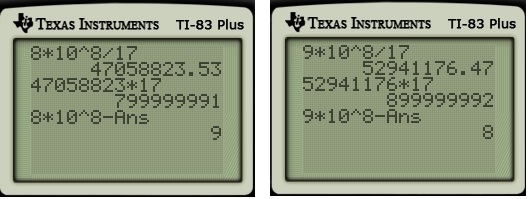
Before cheap pocket calculators, how would someone find $\displaystyle \frac{1}{2 \sqrt{2}} ~~$ or $~~ \displaystyle \frac{ \sqrt{2} }{4}$ to nine decimal places? Clearly, the first step is finding $\sqrt{2}$ by hand, which I discussed in a previous post. So these expressions reduce to

$\displaystyle \frac{1}{2 (1.41421356\dots)}$ or $\displaystyle \frac{1.41421356\dots}{4}$

Next comes the step of dividing. If you don’t have a calculator and had to use long division, which would rather do: divide by $4$ or divide by $2.82842712\dots$ ?

Clearly, long division with $4$ is easier.

It seems to me that ease of computation was the reason that rationalizing denominators was required of students in previous generations. So I’m a little bemused why rationalizing denominators is still required of students now that cheap calculators are so prevalent.

Lest I be misunderstood, I absolutely believe that all students should be able to convert $\displaystyle \frac{1}{2 \sqrt{2}}$ into $\displaystyle \frac{ \sqrt{2} }{4}$ . But I see no compelling reason why the “simplified” answer to the above trigonometry problem should be the second answer and not the first.

Collaborative Mathematics: Challenge 07

My colleague Jason Ermer has posted his 7th challenge video, shown below. It’s both an experiment and an exercise in probability.

Video responses can be posted to his website, http://www.collaborativemathematics.org. In the words of his website, this is a unique forum for connecting a worldwide community of mathematical problem-solvers, and I think these unorthodox but simply stated problems are a fun way for engaging students with the mathematical curriculum.

Engaging students: Vectors in two dimensions

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Derek Skipworth. His topic, from Precalculus: vectors in two dimensions.

A. How could you as a teacher create an activity or project that involves your topic?

While it may be a cop-out to use this example since I am developing it for an actual lesson plan, I will go ahead and use it because I feel it is a strong activity. I am developing a series of 21 problems that will be the base for forming the students’ treasure maps. There will be three jobs: Cartographer, the map maker; Lie Detector, who checks for orthogonality; and Calculator, who will solve the vector problems. The 21 problems will be broken down into 7 per page, and the students will switch jobs after each page. The rule is that any vectors that are orthogonal with each other cannot be included in your map. There are three of these on each page, so each group should end up with a total of 12 vectors on their map. Once orthogonality is checked by the Lie Detector, the Calculator will do the expressed operations on the vector pairs to come up with the vector to be drawn. The map maker will then draw the vector, as well as the object the vector leads to. Each group will have their directions in different orders so that every group has their own unique map. The idea is for the students to realize (if they checked orthogonality correctly) that, even though every map is different, the sum of all vectors still leads you to the same place, regardless of order.

B. How does this topic extend what your students should have learned in previous courses?

Vectors build upon many topics from previous courses. For one, it teaches the student to use the Cartesian plane in a new way than they have done previously. Vectors can be expressed in terms of force in the $x$ and $y$ directions, which result in a representation very similar to an ordered pair. It gets expanded to teach the students that unlike an ordered pair, which represents a distinct point in space, a vector pair represents a specific force that can originate from any point on the Cartesian Plane.

Vectors also build on previous knowledge of triangles. When written as $\langle x,y \rangle$ , we can find the magnitude of the vector by using the Pythagorean Theorem. It gives them a working example of when this theorem can be applied on objects other than triangles. It also reinforces the students trigonometry skills since the direction of a vector can also be expressed using magnitude and angles.

E. How can technology be used to effectively engage students with this topic?

The PhET website has one of the best tools I’ve seen for basic knowledge of two dimensional vector addition, located at http://phet.colorado.edu/en/simulation/vector-addition. This is a java-based program that lets you add multiple vectors (shown in red) in any direction or magnitude you want to get the sum of the vectors (shown in green). Also shown at the top of the program is the magnitude and angle of the vector, as well as its corresponding $x$ and $y$ values.

What’s great about this program is it puts the power in the student’s hands. They are not forced to draw multiple sets of vectors themselves. Instead, they can quickly throw them in the program and manipulate them without any hassle. This effectively allows the teacher to cover the topic quicker and more effectively due to the decreased amount of time needed to combine all vectors on a graph.

Collaborative Mathematics: Challenge 05

My colleague Jason Ermer is back from summer hiatus and has posted his fifth challenge video, shown below.

Thoughts on 1/7 and other rational numbers (Part 10)

In the previous post, I showed a quick way of obtaining a full decimal representation using a calculator that only displays ten digits at a time. To review: here’s what a TI-83 Plus returns as the (approximate) value of $8/17$ :

Using this result and the Euler totient function, we concluded that the repeating block had length $16$ . So we multiply twice by $10^8$ (since $10^8 \times 10^8 = 10^{16}$ ) to deduce the decimal representation, concluding that

$\displaystyle \frac{8}{17} = 0.\overline{4705882352941176}$

Though this is essentially multi-digit long division, most students are still a little suspicious of this result on first exposure. So here’s a second way of confirming that we did indeed get the right answer. The calculators show that

$8 \times 10^8 = 17 \times 47058823 + 9$ and $9 \times 10^8 = 17 \times 52941176 + 8$

Therefore,

$8 \times 10^{16} = 17 \times (47058823 \times 10^8) + 9 \times 10^8$ and $9 \times 10^8 = 17 \times 52941176 + 8$

so that

$8 \times 10^{16} = 17 \times (47058823 \times 10^8) + 17 \times 52941176 + 8$

$8 \times 10^{16} = 17 \times 4705882352941176 + 8$

$8 \times 10^{16} - 8 = 17 \times 4705882352941176$

$8 (10^{16}-1) = 17 \times 4705882352941176$

$\displaystyle \frac{8}{17} = \displaystyle \frac{4705882352941176}{10^{16}-1}$

Using the rule for dividing by $10^k -1$ , we conclude that

$\displaystyle \frac{8}{17} = 0.\overline{4705882352941176}$

Thoughts on 1/7 and other rational numbers (Part 9)

Let’s now consider the decimal representation of $\displaystyle \frac{8}{17}$ .

There’s no obvious repeating pattern. But we know that, since 17 has neither 2 nor 5 as a factor, that there has to be a repeating decimal pattern.

So… what is it?

When I ask this question to my students, I can see their stomachs churning a slow dance of death. They figure that the calculator didn’t give the answer, and so they have to settle for long division by hand.

That’s partially correct.

However, using the ideas presented below, we can perform the long division extracting multiple digits at once. Through clever use of the calculator, we can quickly obtain the full decimal representation even though the calculator can only give ten digits at a time.

Let’s now return to where this series began… the decimal representation of $\displaystyle \frac{1}{7}$ using long division. As shown below, the repeating block has length $6$ , which can be found in a few minutes with enough patience. By the end of this post, we’ll consider a modification of ordinary long division that facilitates the computation of really long repeating blocks.

Because we arrived at a repeated remainder, we know that we have found the repeating block. So we can conclude that $\displaystyle \frac{1}{7} = 0.\overline{142857}$ .

Students are taught long division in elementary school and are so familiar with the procedure that not much thought is given to the logic behind the procedure. The underlying theorem behind long division is typically called the division algorithm. From Wikipedia:

Given two integers $a$ and $b$ , with $b \ne 0$ , there exist unique integers $q$ and $r$ such that $a = bq+r$ and $0 \le r < |b|$, where $|b|$ denotes the absolute value of $b$ .

The number $q$ is typically called the quotient, while the number $r$ is called the remainder.

Repeated application of this theorem is the basis for long division. For the example above:

Step 1.

$10 = 1 \times 7 + 3$ . Dividing by $10$ , $1 = 0.1 \times 7 + 0.3$

Step 2.

$30 = 4 \times 7 + 2$ . Dividing by $100$ , $0.3 = 0.04 \times 7 + 0.02$

Returning to the end of Step 1, we see that

$1 = 0.1 \times 7 + 0.3 = 0.1 \times 7 + 0.04 \times 7 + 0.02 = 0.14 \times 7 + 0.02$

Step 3.

$20 = 2 \times 7 + 6$ . Dividing by $1000$ , $0.02 = 0.002 \times 7 + 0.006$

Returning to the end of Step 2, we see that

$1 = 0.14 \times 7 + 0.02 = 0.14 \times 7 + 0.0002 \times 7 + 0.006 = 0.142 \times 7 + 0.006$

And so on.

By adding an extra zero and using the division algorithm, the digits in the decimal representation are found one at a time. That said, it is possible (with a calculator) to find multiple digits in a single step by adding extra zeroes. For example:

Alternate Step 1.

$1000 = 142 \times 7 + 6$ . Dividing by $1000$ , $1 = 0.142 \times 7 + 0.006$

Alternate Step 2.

$6000 = 587 \times 7 + 1$ . Dividing by $100000$ , $0.006 = 0.000587 \times 7 + 0.000001$

Returning to the end of Alternate Step 1, we see that

$1 = 0.142 \times 7 + 0.006= 0.142 \times 7 + 0.000587\times 7 + 0.000001 = 0.142857 \times 7 + 0.000001$

So, with these two alternate steps, we arrive at a remainder of $1$ and have found the length of the repeating block.

The big catch is that, if $a = 1000$ or $a = 6000$ and $b = 7$ , the appropriate values of $q$ and $r$ have to be found. This can be facilitated with a calculator. The integer part of $1000/7$ and $6000/7$ are the two quotients needed above, and subtraction is used to find the remainders (which must be less than $7$ , of course).

At first blush, it seems silly to use a calculator to find these values of $q$ and $r$ when a calculator could have been used to just find the decimal representation of $1/7$ in the first place. However, the advantage of this method becomes clear when we consider fractions who repeating blocks are longer than 10 digits.

Let’s now return to the question posed at the top of this post: finding the decimal representation of $\displaystyle \frac{8}{17}$ . As noted in Part 6 of this series, the length of the repeating block must be a factor of $\phi(17)$ , where $\phi$ is the Euler toitent function, or the number of integers less than $17$ that are relatively prime with $17$ . Since $17$ is prime, we clearly see that $\phi(17) = 16$ . So we can conclude that the length of the repeating block is a factor of $16$ , or either $1$ , $2$ , $4$ , $8$ , or $16$ .

Here’s the result of the calculator again:

We clearly see from the calculator that the repeating block doesn’t have a length less than or equal to $8$ . By process of elimination, the repeating block must have a length of $16$ digits.

Now we perform the division algorithm to obtain these digits, as before. This can be done in two steps by multiplying by $10^8 = 100,000,000$ .

So, by the same logic used above, we can conclude that

$\displaystyle \frac{8}{17} = 0.\overline{4705882352941176}$

In other words, through clever use of the calculator, the full decimal representation can be quickly found even if the calculator itself returns only ten digits at a time… and had rounded the final $2941176$ of the repeating block up to $3$ .

Calculator errors: When close isn’t close enough (Part 2)

In the previous post, I gave a simple classroom demonstration to illustrate that some calculators only approximate an infinite decimal expansion with a terminating decimal expansion, and hence truncation errors can propagate. This example addresses the common student question, “What’s the big deal if I round off to a few decimal places?”

(For what it’s worth, I’m aware that some current high-end calculators are miniature computer algebra systems and can formally handle an answer of $\displaystyle \frac{1}{3}$ instead of its decimal expansion.)

Students may complain that the above exercise is artificial and unlikely to occur in real life. I would suggest following up with a real-world, non-artificial, and tragic example of an accident that happened in large part due to truncation error. This incident occurred during the first Gulf War in 1991 (perhaps ancient history to today’s students). I’m going to quote directly from the website http://www.ima.umn.edu/~arnold/disasters/patriot.html, published by Dr. Douglas Arnold at the University of Minnesota. Perhaps students don’t need to master the details of this explanation (a binary expansion as opposed to a decimal expansion might be a little abstract), but I think that this example illustrates truncation error vividly.

On February 25, 1991, during the Gulf War, an American Patriot Missile battery in Dharan, Saudi Arabia, failed to track and intercept an incoming Iraqi Scud missile. The Scud struck an American Army barracks, killing 28 soldiers and injuring around 100 other people. A report of the General Accounting office, GAO/IMTEC-92-26, entitled Patriot Missile Defense: Software Problem Led to System Failure at Dhahran, Saudi Arabia reported on the cause of the failure.

It turns out that the cause was an inaccurate calculation of the time since boot due to computer arithmetic errors. Specifically, the time in tenths of second as measured by the system’s internal clock was multiplied by $1/10$ to produce the time in seconds. This calculation was performed using a 24 bit fixed point register. In particular, the value $1/10$ , which has a non-terminating binary expansion, was chopped at 24 bits after the radix point. The small chopping error, when multiplied by the large number giving the time in tenths of a second, led to a significant error.

Indeed, the Patriot battery had been up around 100 hours, and an easy calculation shows that the resulting time error due to the magnified chopping error was about $0.34$ seconds.

The number $1/10$ equals

$\displaystyle \frac{1}{2^4} + \frac{1}{2^5} +\frac{1}{2^8} + \frac{1}{2^9} + \frac{1}{2^{12}} + \frac{1}{2^{13}} + \dots$

In other words, the binary expansion of $1/10$ is

$0.0001100110011001100110011001100....$

Now the 24 bit register in the Patriot stored instead

$0.00011001100110011001100$

introducing an error of

$0.0000000000000000000000011001100...$ binary,

or about $0.000000095$ decimal. Multiplying by the number of tenths of a second in $100$ hours gives

$0.000000095 \times 100 \times 60 \times 60 \times 10=0.34$ .

A Scud travels at about $1,676$ meters per second, and so travels more than half a kilometer in this time. This was far enough that the incoming Scud was outside the “range gate” that the Patriot tracked.

Ironically, the fact that the bad time calculation had been improved in some parts of the code, but not all, contributed to the problem, since it meant that the inaccuracies did not cancel.

The following paragraph is excerpted from the GAO report.

The range gate’s prediction of where the Scud will next appear is a function of the Scud’s known velocity and the time of the last radar detection. Velocity is a real number that can be expressed as a whole number and a decimal (e.g., 3750.2563…miles per hour). Time is kept continuously by the system’s internal clock in tenths of seconds but is expressed as an integer or whole number (e.g., 32, 33, 34…). The longer the system has been running, the larger the number representing time. To predict where the Scud will next appear, both time and velocity must be expressed as real numbers. Because of the way the Patriot computer performs its calculations and the fact that its registers are only 24 bits long, the conversion of time from an integer to a real number cannot be any more precise than 24 bits. This conversion results in a loss of precision causing a less accurate time calculation. The effect of this inaccuracy on the range gate’s calculation is directly proportional to the target’s velocity and the length of the the system has been running. Consequently, performing the conversion after the Patriot has been running continuously for extended periods causes the range gate to shift away from the center of the target, making it less likely that the target, in this case a Scud, will be successfully intercepted.

A quick note of clarification. To verify the binary expansion of $1/10$ , we use the formula for an infinite geometric series.

$S = \displaystyle \left(\frac{1}{2^4} + \frac{1}{2^5}\right) +\left(\frac{1}{2^8} + \frac{1}{2^9}\right) + \left(\frac{1}{2^{12}} + \frac{1}{2^{13}}\right) + \dots$

$S = \displaystyle \frac{3}{2^5} + \frac{3}{2^9} + \frac{3}{2^{13}} + \dots$

$S = \displaystyle \frac{\displaystyle \frac{3}{2^5}}{\quad \displaystyle 1 - \frac{1}{2^4} \quad}$

$S = \displaystyle \frac{\displaystyle \frac{3}{32}}{\quad \displaystyle \frac{15}{16} \quad}$

$S = \displaystyle \frac{3}{32} \times \frac{16}{15}$

$S = \displaystyle \frac{1}{10}$

OK, that verifies the answer. Still, a curious student may wonder how one earth one could directly convert $1/10$ into binary without knowing the above series ahead of time. I will address this question in a future post.

Calculator errors: When close isn’t close enough (Part 1)

Far too often, students settle for a numerical approximation of a solution that can be found exactly. To give an extreme example, I have met quite intelligent college students who were convinced that $\displaystyle \frac{1}{3}$ was literally equal to $0.3$ .

That’s an extreme example of something that nearly all students do — round off a complicated answer to a fixed number of decimal places. In trigonometry, many students will compute $\sin \left( \cos^{-1} 0.3 \right)$ by plugging into a calculator and reporting the first three to six decimal places, like $0.95394$ . This is especially disappointing when there are accessible techniques for getting the exact answer (in this case, $\displaystyle \frac{\sqrt{91}}{10}$ ) without using a calculator at all.

Unfortunately, even maintaining eight, nine, or ten decimal places of accuracy may not be good enough, as errors tend to propagate as a calculation continues. I’m sure every math teacher has an example where the correct answer was exactly $\displaystyle\frac{3}{2}$ but students returned an answer of $1.4927$ or $1.5031$ because of roundoff errors.

Students may ask, “What’s the big deal if I round off to five decimal places?” Here’s a simple example — which can be quickly demonstrated in a classroom — of how such truncation errors can propagate. I’m going to generate a recursive sequence. I will start with $\displaystyle \frac{1}{3}$ . Then I will alternate multiplying by $1000$ and then subtracting $333$ . More mathematically,

$a_1 = \displaystyle \frac{1}{3}$

$a_{2n} = 1000 a_{2n-1}$

$a_{2n+1} = a_{2n} - 333$ if $n > 0$

Here’s what happens exactly:

$1000 \times \displaystyle \frac{1}{3} = \displaystyle \frac{1000}{3} = \displaystyle 333\frac{1}{3} = 333.\overline{3}$

$\displaystyle 333\frac{1}{3} - 333 = \displaystyle \frac{1}{3} = 0.\overline{3}$

So, repeating these two steps, the sequence alternates between $\displaystyle \frac{1}{3}$ and $\displaystyle 333\frac{1}{3}$ .

But looks what happens if I calculate the first twelve terms of this sequence on a calculator.

Notice that by the time I reach $a_{11}$ , the terms of the sequence are negative, which is clearly incorrect.

So what happened?

This is a natural by-product of the finite storage of a calculator. The calculator doesn’t store infinitely many digits of $\displaystyle \frac{1}{3}$ in memory because a calculator doesn’t possess an infinite amount of memory. Instead, what gets stored is something like the terminating decimal $0.33333333333333$ , with about fourteen $3$ s. (Of course, only the first ten digits are actually displayed.)

So multiplying by $1000$ and then subtracting $333$ produces a new and different terminating decimal with three less $3$ s. Do this enough times, and you end up with negative numbers.

Square roots with a calculator (Part 11)

This is the last in a series of posts about square roots and other roots, hopefully providing a deeper look at an apparently simple concept. However, in this post, we discuss how calculators are programmed to compute square roots quickly.

Today’s movie clip, therefore, is set in modern times:

So how do calculators find square roots anyway? First, we recognize that $\sqrt{a}$ is a root of the polynomial $f(x) = x^2 - a$ . Therefore, Newton’s method (or the Newton-Raphson method) can be used to find the root of this function. Newton’s method dictates that we begin with an initial guess $x_1$ and then iteratively find the next guesses using the recursively defined sequence

$x_{n+1} = x_n - \displaystyle \frac{f(x_n)}{f'(x_n)}$

For the case at hand, since $f'(x) = 2x$ , we may write

$x_{n+1} = x_n - \displaystyle \frac{x_n^2 -a}{2 x_n}$ ,

which reduces to

$x_{n+1} = \displaystyle \frac{2x_n^2 - (x_n^2 -a)}{2 x_n} = \frac{x_n^2 + a}{2x_n} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right)$

This algorithm can be programmed using C++, Python, etc.. For pedagogical purposes, however, I’ve found that a spreadsheet like Microsoft Excel is a good way to sell this to students. In the spreadsheet below, I use Excel to find $\sqrt{2000}$ . In cell A1, I entered $1000$ as a first guess for $\sqrt{2000}$ . Notice that this is a really lousy first guess! Then, in cell A2, I typed the formula

=1/2*(A1+2000/A1)

So Excel computes

$x_2 = \frac{1}{2} \left( x_1 + \displaystyle \frac{2000}{x_1} \right) = \frac{1}{2} \left( 1000 + \displaystyle \frac{2000}{1000} \right) = 501$ .

Then I filled down that formula into cells A3 through A16.

Notice that this algorithm quickly converges to $\sqrt{2000}$ , even though the initial guess was terrible. After 7 steps, the answer is only correct to 2 significant digits ( $45$ ). After 8 steps, the answer is correct to 4 significant digits ( $44.72$ ). On the 9th step, the answer is correct to 9 significant digits ( $44.7213595$ ).

Indeed, there’s a theorem that essentially states that, when this algorithm converges, the number of correct digits basically doubles with each successive step. That’s a lot better than the methods shown at the start of this series of posts which only produced one extra digit with each step.

This algorithm works for finding $k$ th roots as well as square roots. Since $\sqrt[k]{a}$ is a root of $f(x) = x^k - a$ , Newton’s method reduces to

$x_{n+1} = x_n - \displaystyle \frac{x_n^k - a}{k x_n^{k-1}} = \displaystyle \frac{(k-1) x_n^k + a}{k x_n^{k-1}} = \displaystyle \frac{k-1}{k} x_k + \frac{1}{k} \cdot \frac{a}{x_n}$ ,

which reduces to the above sequence if $k =2$ .

See also this Wikipedia page for further historical information as well as discussion about how the above recursive sequence can be obtained without calculus.

Engaging students: Box and whisker plots

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This submission comes from my former student Jesse Faltys. Her topic: how to engage students when teaching box and whisker plots.

A. Applications – How could you as a teacher create an activity or project that involves your topic?

Students can take a roster of a professional basketball team and create a box and whiskers plot by using the players’ stats of height and weight. As the teacher, you can provide these numbers to them. The weight should be left in pounds, but change the height measurement to inches. The students could be placed in groups of 3 or 4 and given different team rosters. First, have the student calculate the minimum, maximum, lower quartile, upper quartile, and median for their roster for both the weight and height. Then, have the students place the plots on large sheets of paper and present to the class. As the students compare their plots, they can begin to see what effects the range of data has on the construction of each box and whisker plot. Depending on the knowledge of the students you might want them to all working on the same team. As the teacher, you can remove one player’s stats from each group effectively changing the box and whiskers plots and having the students analyzing the data’s effect on the plot constructed from the same roster.

I actually used this in a lesson during my Step II class in a middle school classroom. I used information from the Illuminations website at http://illuminations.nctm.org/LessonDetail.aspx?ID=L737.

B. Curriculum – How can this topic be used in your students’ future courses in mathematics or science?

Any science course with a lab will require you to complete a formal lab write-up. The data collected from your experiment will need to be represented in an organized manner. The features of a box-and-whiskers plot will allow you to gather all your information and make observations off the data that your group and the class as a whole collected. This information can be combined into one plot or the individual lab groups can be compared for any inconsistencies. A box-and-whisker plot can be useful for handling many data values. It shows only certain statistics rather than all the data. Five-number summary is another name for the visual representations of the box-and-whisker plot. The five-number summary consists of the median, the quartiles, and the smallest and greatest values in the distribution. Immediate visuals of a box-and-whisker plot are the center, the spread, and the overall range of distribution. This documentation will allow the student to make a formal analysis while putting together their formal lab write-up.

E. Technology – How can technology be used to effectively engage students with this topic?

1. Khan Academy provides a video titled “Reading Box-and-Whisker Plots” which shows an example of a collection of data on the age of trees. The instructor on the video goes through the representations of the different parts of the structure of the box and whiskers plot. For our listening learners, this reiterates to the student what the plot is summarizing. http://www.khanacademy.org/math/probability/descriptive-statistics/Box-and-whisker%20plots/v/reading-box-and-whisker-plots

2. Math Warehouse allows you to enter the data you are using and it will calculate the plot for you. After having the students work on their own plots, you can have them check their work for themselves. This will allow for immediate confirmation if the student is creating the graph correctly with the data provided. Also, this is allowing the visual learners to see what happens to the length of the box or whiskers when changes are made to the minimum, maximum or median. http://www.mathwarehouse.com/charts/box-and-whisker-plot-maker.php#boxwhiskergraph

3. The Brainingcamp is another website that allows for interaction between the different parts of the plot and the student. This website allows for the students to see a group of data and the matching box-and-whiskers plot. The student can then explore by manually changing different values and instantly seeing a change in the graph. This involvement can stimulate questions to direct the student to complete understanding of the subject. As a hands on learner, it allows the students to manipulate the plot immediately in different “what if” situations. http://www.brainingcamp.com/resources/math/box-plots/interactive.php