In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.
I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).
This student submission again comes from my former student Chais Price. His topic, from Algebra: the quadratic formula.
What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?
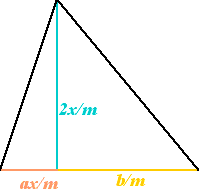
What is the quadratic formula you ask? It is basically a tool used to find roots of the quadratic equation. It all started around 3000 BC,when the Ancient Babylonians needed a method for calculating how much to pay the tax collector. Imagine that you are an Ancient Babylonian farmer with a square field that is placed in the middle of your farm. On this field you plan to plant some crops. After some experimenting you discover that if you double the length of each side of the square field, you end up with 4 times as many crops as before. This observation demonstrated the area of the field and the amount of crops that you can grow and the square of one of the side lengths are all proportional. From here we come up with the first quadratic equation. Let “x” represent the length of a side and “m” be the amount of crops you can grow on a square field of side length 1. Then we have “c” which is the entire area of crop that can be grown. Thus c= mx^2. It is now April 15 in Babylonia and the tax collector comes and says to give him “c” crops to pay your taxes. Now you ask yourself, how big does your square field need to be to grow that amount of crops? Well as it turns out, we just take x= (c/m)^1/2. The Babylonians however, did not have a way to solve square roots accurately. They were just estimations. This square field representation is just a basic representation. Let’s say that your field was not a square but a triangle divided into 2 right triangles where a and b are the amount of crops that you can grow in each field.
To calculate the amount of crops, you being a very intelligent Babylonian farmer, you come up with the equation
.
The next step is to divide by “a” and then complete the square yielding
Now we substitute into the previous equation. We now have an equation of the form
Solving again for the tax collector, we need to solve for “x.” This gives us what we know as the quadratic formula:
Something worth noting since you are an Ancient Babylonian farmer, is that all the roots you find are positive since negative numbers have not been discovered yet. In addition, the quadratic formula shown above is just an illustration broken down step by step. The Babylonians had no general formula for the quadratic formula, but there method for the quadratic formula can be closely associated with the method of completing the square.
How has this topic appeared in the news?
There is a pretty interesting article I read which had to do with the quadratic equation. A teacher provided a list of quadratic equations that the students would pick from. This equation was to be to model for a parabolic device that the student was responsible for building. The student was instructed to spend no more than 12 dollars on this project. They would use the equation to calculate a positional focus which suspended a marshmallow which would cook slowly due to the rays of the sun reflected upon it. This lesson stretched using a quadratic equation to form a focus. Then the student would graph the data and calculate the rate of temperature increase. Student were also asked to make predictions on what temperature the marshmallow would get to. Once the experiment is complete, the student is anxious to see how accurate their model is to the actual equation they chose. This is a very good lesson that covers a pretty broad range of topics.
So the concept of the quadratic formula would develop beyond what the Ancient Babylonians discovered. 1500 years after the Babylonians, the Egyptians came along with a different approach for similar type problems where the quadratic formula was used. The mathematics behind the calculations were known to be very complicated. However, they recorded these calculation on a table ( much like our multiplication tables) so that when a farmer or an engineer required some kind of proportion or dimensional measurement using the quadratic formula, rather than solving the problem again, they would just look it up on the table that had already been calculated. They reproduced this table and made it a master look up guide to follow for such solutions.
Then the Babylonians would reappear in time and discover the method of completing the square. This method still required somewhat of an educated guess. However, since the Babylonians had a 60 base numerical system ( which the Egyptians did not) addition and multiplication were easier to compute and check calculations. Even still there was not a general formula or equation established. Then Pythagoras and Euclid came along and developed a general formula to solve the quadratic equation. Pythagoras argued that the ratio of the area of a square and the length of a side does not always produce an integer and indeed can have a rational solution. Euclid advanced beyond Pythagoras and claimed you could have irrational results. These were logical claims made from a theoretical point of view because at that time there was no way to calculate the square root of a number by hand. Finally in 700 AD, a mathematician named Brahmagupta from India came up with a general solution to the quadratic equation using numbers. He also was on board with Euclid and his irrationals as well as an equation producing 2 roots. His work more than likely inspired another Hindu Mathematician named Baskhara who around 1100 AD formulated the complete solution we are familiar with today. He was also the first to acknowledge that any number greater than 0 has 2 square roots. It was around this same time in history that a Jewish mathematician Abraham bar Hiyya derived the quadratic formula and brought it to Europe. It wouldn’t be until another 500 years that the quadratic formula would be adopted into the formula we know today.
Works Cited
Budd, Chris, and Chris Sangwin. “101 Uses of the Quadratic Equation.” Plus Math. Plus Magazine… Living Mathematics , 01 Mar 2004. Web. 10 Sep 2014. http://plus.maths.org/content/101-uses-quadratic-equation
Tracey, Wong Briggs. “Students use quadratic equations to cook marshmallows.” USA Today. USA Today, 05 Mar 2007. Web. 10 Sep 2014. http://usatoday30.usatoday.com/news/education/2007-03-04-teacher-parabola-side_N.htm?csp=34
Hell, Dr. . “The History Behind the Quadratic Formula .” . BBC H2G2, 13 October 2004. Web. 10 Sep 2014. http://news.bbc.co.uk/dna/place-lancashire/plain/A2982567