Category: Humor

My Favorite One-Liners: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The links below show my series on my favorite one-liners.

Mathematical Wisecracks for Almost Any Occasion: Part 2,  Part 7, Part 8, Part 12, Part 21, Part 28, Part 29, Part 41, Part 46, Part 53, Part 60, Part 63, Part 65, Part 71, Part 79, Part 84, Part 85, Part 100, Part 101,  Part 108, Part 109, Part 114, Part 118, Part 121

All-Purpose Anecdotes: Part 38, Part 50, Part 64, Part 70, Part 92, Part 94

Addressing Misconceptions: Part 3, Part 4, Part 11, Part 14, Part 15, Part 18, Part 30, Part 32, Part 33, Part 37, Part 45, Part 59

Tricky Steps in a Calculation: Part 5, Part 6

Greek alphabet and choice of variables: Part 40, Part 43, Part 56

Homework and exams: Part 39, Part 47, Part 55, Part 57, Part 58, Part 66, Part 77, Part 78, Part 91, Part 96, Part 97, Part 107

Inequalities: Part 99

Simplification: Part 10, Part 102, Part 103

Polynomials: Part 19, Part 48, Part 49, Part 81, Part 90

Inverses: Part 16

Exponential and Logarithmic Functions: Part 1, Part 42, Part 68, Part 80, Part 110

Trigonometry: Part 9, Part 69, Part 76, Part 106, Part 120

Complex numbers: Part 54, Part 67, Part 86, Part 112, Part 113

Sequences and Series: Part 20, Part 35, Part 111

Combinatorics: Part 27

Statistics: Part 22, Part 23, Part 36, Part 51, Part 52, Part 61, Part 95, Part 116

Probability: Part 26, Part 31, Part 62, Part 93, Part 122

Calculus: Part 24, Part 25, Part 72, Part 73, Part 74, Part 75, Part 83, Part 87, Part 88, Part 104, Part 115, Part 117

Logic and Proofs: Part 13, Part 17, Part 34, Part 44, Part 89, Part 98, Part 119

Differential Equations: Part 82, Part 105

A Postcard from Spokane

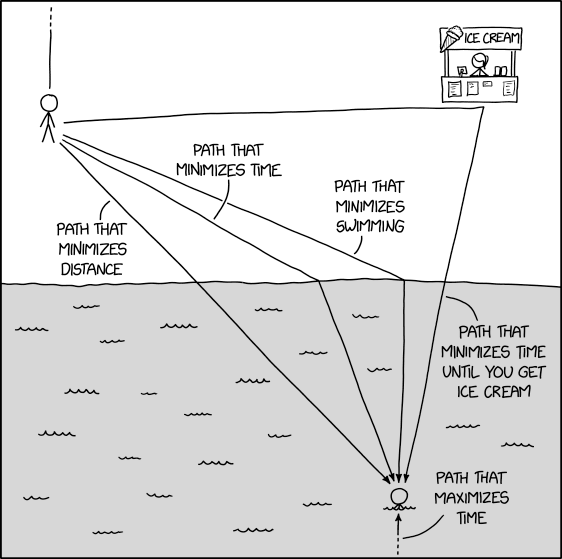
A brief aside from the current series on general relativity — and the mysterious 43 seconds of arc per century in Mercury’s orbit — that turned into further discussion about angle measurement.

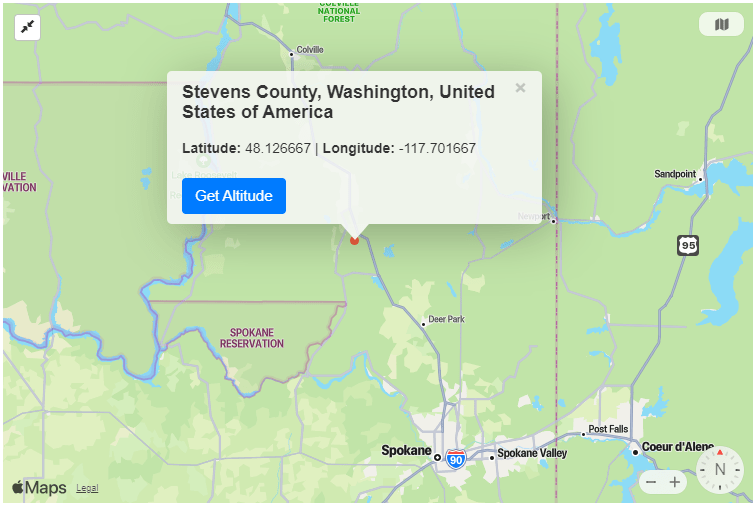
A few months ago, I received this clever postcard from someone visiting Spokane, Washington. The sender clearly knew the recipient (me) well: rather than sending me a postcard showing the jaw-dropping beauty of the Spokane area, I was impressed with the mathematical precision given for Spokane’s location.

I started wondering about exactly how precisely the postcard was measuring the location of Spokane — was it the location of City Hall or some other important landmark? — and I went to Google Maps to find out. (For what it’s worth, xkcd had a comic about this some time ago.)

And then it finally hit me, after far longer than it should have taken, that the postcard is utterly nonsensical.

We would never say that someone’s height is 4 feet, 20 inches. There are 12 inches in a foot, and so we would instead say that the height is 5 feet, 8 inches.

Likewise, when specifying an angle with minutes and seconds, there are (just like with ordinary time) 60 seconds in a minute and 60 minutes in a degree (so that there are 3600 seconds in a degree). Therefore, specifying an angle with 67′ or 66″, as in the postcard, makes absolutely no sense.

Furthermore, if converted into standard notation, we obtain a location of 48^{\circ} 7' 36'' north, 117^{\circ} 42' 6'' west, which is about 40 miles NNW of Spokane. (Images made by https://www.gps-coordinates.net/). Note on the conversion into decimal:

47 + \displaystyle \frac{67}{60} + \displaystyle \frac{36}{3600} = 48 + \displaystyle \frac{7}{60} + \displaystyle \frac{36}{3600} = 48.12666\dots

and

117 + \displaystyle \frac{41}{60} + \displaystyle \frac{66}{3600} = 117 + \displaystyle \frac{42}{60} + \displaystyle \frac{6}{3600} = 117.701666\dots

It’s a shame that the designer of the postcard made this error, as I genuinely thought this was a clever and aesthetically pleasing design idea for a postcard.

While I’m not sure how this mistake happened, my best guess is that the designer used the location of 47.6736^\circ north, 117.4166^\circ west — which is indeed in Spokane — and then misconverted from decimal notation to minutes and seconds.