Category: Elementary

Lessons from teaching gifted elementary school students (Part 6a)

Every so often, I’ll informally teach a class of gifted elementary-school students. I greatly enjoy interacting with them, and I especially enjoy the questions they pose. Often these children pose questions that no one else will think about, and answering these questions requires a surprising depth of mathematical knowledge.

Here’s a question I once received:

255/256 to what power is equal to 1/2? And please don’t use a calculator.

Answering this question is pretty straightforward using algebra:

\displaystyle \left( \frac{255}{256} \right)^x = \displaystyle \frac{1}{2}.

\displaystyle x \ln  \frac{255}{256} = \ln \displaystyle \frac{1}{2}

x \displaystyle \frac{ \displaystyle \ln \frac{1}{2} }{\ln \displaystyle \frac{255}{256}}

However, doing this without a calculator — and thus maintaining my image in front of these elementary school students — is a little formidable.

I’ll reveal how I did this — getting the answer correct to the nearest integer — in tomorrow’s post. In the meantime, I’ll leave a thought bubble if you’d like to think about it on your own.

green_speech_bubble

A curious non-randomness in the distribution of primes

I found this article extremely interesting. From https://www.quantamagazine.org/20160313-mathematicians-discover-prime-conspiracy/

Among the first billion prime numbers, for instance, a prime ending in 9 is almost 65 percent more likely to be followed by a prime ending in 1 than another prime ending in 9. In a paper posted online today [March 13, 2016], Kannan Soundararajan and Robert Lemke Oliver of Stanford University present both numerical and theoretical evidence that prime numbers repel other would-be primes that end in the same digit, and have varied predilections for being followed by primes ending in the other possible final digits…

This conspiracy among prime numbers seems, at first glance, to violate a longstanding assumption in number theory: that prime numbers behave much like random numbers. Most mathematicians would have assumed… that a prime should have an equal chance of being followed by a prime ending in 1, 3, 7 or 9 (the four possible endings for all prime numbers except 2 and 5).

Another Poorly Written Word Problem: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series poorly written word problem, taken directly from textbooks and other materials from textbook publishers.

Part 1: Addition and estimation.

Part 2: Estimation and rounding.

Part 3: Probability.

Part 4: Subtraction and estimation.

Part 5: Algebra and inequality.

Part 6: Domain and range of a function.

Part 7: Algebra and inequality.

Part 8: Algebra and inequality.

 

 

My Mathematical Magic Show: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. Here’s my series on the mathematical magic show that I’ll perform from time to time.

Part 1: Introduction.

Part 2a, 2b, and 2c: The 1089 trick.

Part 3a, 3b, and 3c: A geometric magic trick (see also here).

Part 4a, 4b, 4c, and 4d: A trick using binary numbers.

Part 5a, 5b, 5c, 5d: Predicting a digit that’s been erased from a number.

Part 6: Finale.

Part 7: The Fitch-Cheney 5-card trick.

Part 8a, 8b, 8c: A trick using Pascal’s triangle.

 

Thoughts on the Accidental Fraction Brainbuster

I really enjoyed reading a recent article on Math With Bad Drawings centered on solving the following problem without a calculator:

I won’t repeat the whole post here, but it’s an excellent exercise in numeracy, or developing intuitive understanding of numbers without necessarily doing a ton of computations. It’s also a fun exercise to see how much we can figure out without resorting to plugging into a calculator. I highly recommend reading it.

When I saw this problem, my first reflex wasn’t the technique used in the post. Instead, I thought to try the logic that follows. I don’t claim that this is a better way of solving the problem than the original solution linked above. But I do think that this alternative solution, in its own way, also encourages numeracy as well as what we can quickly determine without using a calculator.

Let’s get a common denominator for the two fractions:

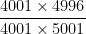\displaystyle \frac{3997 \times 5001}{4001 \times 5001} \qquad and \displaystyle \qquad \frac{4001 \times 4996}{4001 \times 5001}.

Since the denominators are the same, there is no need to actually compute 4001 \times 5001. Instead, the larger fraction can be determined by figuring out which numerator is largest. At first glance, that looks like a lot of work without a calculator! However, the numerators can both be expanded by cleverly using the distributive law:

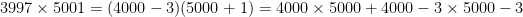3997 \times 5001 = (4000-3)(5000+1) = 4000\times 5000 + 4000 - 3 \times 5000 - 3,

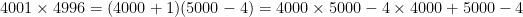4001 \times 4996 = (4000+1)(5000-4) = 4000\times 5000 - 4 \times 4000 + 5000 - 4.

We can figure out which one is bigger without a calculator — or even directly figuring out each product.

  • Each contains 4000 \times 5000, so we can ignore this common term in both expressions.
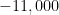  • Also, 4000 - 3\times 5000 and 5000 - 4 \times 4000 are both equal to -11,000, and so we can ignore the middle two terms of both expressions.
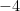  • The only difference is that there’s a -3 on the top line and a -4 on the bottom line.

Therefore, the first numerator is the larger one, and so 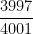\displaystyle \frac{3997}{4001} is the larger fraction.

Once again, I really like the original question as a creative question that initially looks intractable that is nevertheless within the grasp of middle-school students. Also, I reiterate that I don’t claim that the above is a superior method, as I really like the method suggested in the original post. Instead, I humbly offer this alternate solution that encourages the development of numeracy.

My Mathematical Magic Show: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The links below show the mathematical magic show that I’ll perform from time to time.

Part 1: Introduction.

Part 2a, Part 2b, and Part 2c: The 1089 trick.

Part 3a, Part 3b, and Part 3c: A geometric magic trick.

Part 4a: Part 4b, Part 4c, and Part 4d: A trick using binary numbers.

Part 5a, Part 5b, Part 5c, and Part 5d: A trick using the rule for checking if a number is a multiple of 9.

Part 7: The Fitch-Cheney card trick, which is perhaps the slickest mathematical card trick ever devised.

Part 8a, Part 8b, and Part 8c: A trick using Pascal’s triangle.

Part 6: The Grand Finale.

And, for the sake of completeness, here’s a recent picture of me just before I performed an abbreviated version of this show for UNT’s Preview Day for high school students thinking about enrolling at my university.

magician

 

A nice subtraction trick

A friend of mine recently posted this trick for subtracting any number from any multiple of 10^n. (I discovered this trick when I was a boy and have been using it ever since.)

Pedagogically, I don’t think I’d recommend requiring every elementary school student to learn this trick. But this does make a nice enrichment activity for talented elementary school students, as it requires conceptual understanding of subtraction and not just the ability to follow a procedure.

 

 

Subtraction Trick 1

Source: https://www.facebook.com/australianteachers/photos/a.1409177146069885.1073741828.1409169412737325/1505873516400247/?type=3&theater

Here’s another approach, taken from the comments of the above webpage: consider 5000 as 500 groups of 10 and 0 groups of 1, and then regroup.

 

Subtraction Trick 2