Inverse Functions: Arcsine and Pedagogy (Part 11)

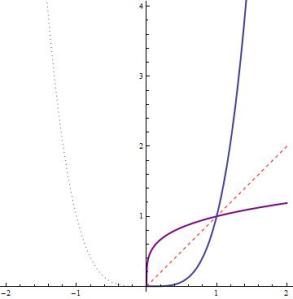
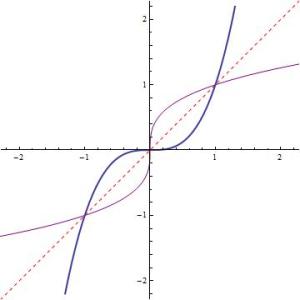
In yesterday’s post, we saw that restricting the domain of $g(x) = \sin x$ to $[-\pi/2,\pi/2]$ permits the definition of $g^{-1}(x) = \sin^{-1} x$ , shown in the purple graph.

Today, I want to give some pedagogical thoughts on teaching this concept to Preaclculus students.

1. Notice that, if the purple graph was completed upward or downward, anything more than a half-period would violate the vertical line test and thus fail to be a function. Thinking back to the original function, that’s another way of saying that the original sine wave violates the horizontal line test.

2. Restricting the domain to $[-\pi/2,\pi/2]$ was a perfectly arbitrary decision. As shown above, there are plenty of other domains that would have worked acceptably. Only tradition requires us to choose $[-\pi/2,\pi/2]$ . (By the way, finding an expression for the restriction of $f$ to, say, $[\pi/2,3\pi/2]$ is a standard problem in a first course in real analysis.)

3. Since $\sin^2 x$ is typically used as shorthand for $(\sin x)^2$ , some students will make the natural mistake of thinking that $\sin^{-1} x$ is just shorthand for $(\sin x)^{-1}$ , or $\csc x$ . So I like to address this head-on when introducing inverse trigonometric functions for the first time to my Precalculus students.

4. Unlike other inverse functions, it can be a little tricky for students to draw the graph of $y = \sin^{-1} x$ by hand because the line of reflection $y =x$ actually is the linearization of $y = \sin x$ at $x = 0$ . In other words, $y = x$ is the first term of the Taylor series of $y = \sin x$ at $x = 0$ . (For more details, see https://meangreenmath.com/2013/07/24/taylor-series-without-calculus-2/ or https://meangreenmath.com/2013/07/06/reminding-students-about-taylor-series-part-6/) Therefore, as seen in the picture, the line $y =x$ is very, very close to the graph of $y = \sin x$ for $x \approx 0$ .

To assist students with accurately drawing by hand the graph of $y = \sin^{-1} x$ , I point out that the original function $y = \sin x$ levels off horizontally at the points $(-\pi/2,-1)$ and $(\pi/2,1)$ . Therefore, after reflecting through the line $y = x$ , the graph of $y = \sin^{-1} x$ enters almost vertically through the points $(-1,-\pi/2)$ and $(1,\pi/2)$ .

5. Most Precalculus students are not savvy enough to appreciate the nuances of domain and range in the above definitions. Therefore, after illustrating the importance of choosing an interval that satisfies the horizontal line test, I’ll give the following ways of remembering what $\sin^{-1} x$ means:

“Arcsine of $x$ is an angle. It is the angle whose sine is equal to $x$ . And it’s the angle that lies between $-\pi/2$ and $\pi/2$ .

$y = \sin^{-1} x$ means that $x = \sin y$ and $-\pi/2 \le y \le \pi/2$ .

6. Since $g: [-\pi,2,\pi/2] \to [-1,1]$ and $g^{-1}: [-1,1] \to [-\pi/2,\pi/2]$ are inverse functions, it’s always true that $g(g^{-1}(x)) = x$ and $g^{-1}(g(x)) = x$ . However, $g^{-1}$ and $f$ are not inverse functions, where $f: \mathbb{R} \to [-1,1]$ is the full sine function $f(x) = \sin x$ . Therefore, it’s possible for $g^{-1}(f(x))$ to be something other than $x$ . For example,

$\sin^{-1} (\sin \pi) = \sin^{-1} (0) = 0 \ne \pi$

$\sin^{-1} \left( \sin \displaystyle \frac{5\pi}{6} \right) = \sin^{-1} \left(\displaystyle \frac{1}{2} \right) = \displaystyle \frac{\pi}{6} \ne \displaystyle \frac{5\pi}{6}$

This is analogous to our earlier observation involving the square root function, which was also defined by a restricted domain:

$\sqrt{(-3)^2} = \sqrt{9} = 3 \ne -3$ .

Inverse Functions: Arcsine (Part 10)

Let’s now switch from functions of the form $y= x^{m/n}$ to the trigonometric functions. We begin with $y = \sin x$ . We will define the function $y = \sin^{-1} x$ using much of the same reasoning that defined $\sqrt{x}$ .

We begin by looking at the graph of $y = \sin x$ .

Of course, we can’t find an inverse for this function as stated. Colloquially, the graph of $f$ fails the horizontal line test. More precisely, there exist two numbers $x_1$ and $x_2$ so that $x_1 \ne x_2$ but $f(x_1) = f(x_2)$ . Indeed, there are infinitely many such pairs.

So how will we find the inverse of $f$ ? Well, we can’t. But we can do something almost as good: we can define a new function $g$ that’s going look an awful lot like $f$ . As before, we will restrict the domain of this new function $g$ so that $g$ satisfies the horizontal line test.

When we did this for the square root function, there were two natural choices for the restricted domain: either $[0,\infty)$ or $(-\infty,0]$ . However, for the sine function, there are plenty of good options from which to choose. Indeed, here are four legitimate options just using the two periods of the sine function shown above. The fourth option is unorthodox, but it nevertheless satisfies the horizontal line test (as long as we’re careful with $\pm 2\pi$ .

So which of these options should we choose? Historically, mathematicians have settled for the interval $[-\pi/2, \pi/2]$ . Why did they settle on this interval? That I can answer with one word: tradition.

So we use the following bijective function (or, using the language that I used when I was a student, a one-to-one and onto function):

$g: [-\pi/2,\pi/2] \to [0,1]$ defined by $g(x) = \sin x$ .

Since this is a bijection, it has an inverse function

$g^{-1}: [0,1] \to [-\pi/2,\pi/2]$

This inverse function is usually denoted as $y = \sin^{-1} x$ or $y = \arcsin x$ . The graph of $y = \sin^{-1} x$ can be produced by reflecting through the line $y=x$ , producing the purple graph below.

One other important note: since $g$ and $g^{-1}$ are inverse functions, it’s always true that $g(g^{-1}(x)) = x$ and $g^{-1}(g(x)) = x$ . However, $g^{-1}$ and $f$ are not inverse functions, and so it’s possible for $g^{-1}(f(x))$ to be something other than $x$ . This parallels the observation that, say, $\sqrt{(-3)^2}$ is not equal to $3$ . We’ll discuss this further in future posts.

Inverse Functions: Arcsine (Part 9)

I’d like to discuss a common mistake students make in trigonometry… as well as the one-liner that I use to (hopefully) help students not make this mistake in the future.

Question. Find all solutions (rounded to the nearest tenth of a degree) of $\sin x = 0.8$ .

Erroneous Solution. Plugging into a calculator, we find that $x \approx 53.1^o$ .

I offer a thought bubble if you’d like to think about why this answer is wrong.

The student correctly found the unique angle $x$ between $-90^o$ and $90^o$ so that $\sin x = 0.8$ . That’s the definition of the arcsine function. However, there are plenty of other angles whose sine is equal to $0.7$ . This can happen in two ways.

First, if $\sin x > 0$, then the angle $x$ could be in either the first quadrant or the second quadrant (thanks to the mnemonic All Scholars Take Calculus). So $x$ could be (accurate to one decimal place) equal to either $53.1^o$ or else $180^o - 53.1^o = 126.9^o$ . Students can visualize this by drawing a picture, talking through each step of its construction (first black, then red, then brown, then green, then blue).

However, most students really believe that there’s a second angle that works when they see the results of a calculator.

Second, any angle that’s coterminal with either of these two angles also works. This can be drawn into the above picture and, as before, confirmed with a calculator.

So the complete answer (again, approximate to one decimal place) should be $53.1^{\circ} + 360n^o$ and $126.9 + 360n^{\circ}$, where $n$ is an integer. Since integers can be negative, there’s no need to write $\pm$ in the solution.

Therefore, the student who simply answers $53.1^o$ has missed infinitely many solutions. The student has missed every nontrivial angle that’s coterminal with $53.1^o$ and also every angle in the second quadrant that also works.

Here’s my one-liner — which never fails to get an embarrassed laugh — that hopefully helps students remember that merely using the arcsine function is not enough for solving problems such as this one.

You’ve forgotten infinitely many solutions. So how many points should I take off?

Inverse Functions: Rational Exponents (Part 8)

In this series of posts, we have seen that the definition of $\sqrt[n]{x}$ and saw that the definition was a little different depending if $n$ is even or odd:

If $n$ is even, then $y = \sqrt[n]{x}$ means that $x = y^n$ and $y \ge 0$ . In particular, this is impossible (for real $y$ ) if $x < 0$ .
If $n$ is odd, then $y = \sqrt[n]{x}$ means that $x = y^n$ . There is no need to give a caveat on the possible values of $y$ .

Let’s now consider the definition of $x^{m/n}$ , where $m$ and $n$ are positive integers greater than 1. Ideally, we’d like to simply defined

$x^{m/n} = \left[ x^{1/n} \right]^m$

This definition reduces to previous work (like a good MIT freshman), using prior definition for raising to powers that are either integers or reciprocals of integers. Indeed, if $x \ge 0$ , there is absolutely no ambiguity about this definition.

Unfortunately, if $x < 0$ , then a little more care is required. There are four possible cases.

Case 1. $m$ and $n$ are odd. In this case, there is no ambiguity if $x < 0$ is negative. For example,

$(-32)^{3/5} = \left[ (-32)^{1/5} \right]^3 = [-2]^3 = -8$

Case 2: $m$ is even but $n$ is odd. Again, there is no ambiguity if $x< 0$ is negative. For example,

$(-32)^{4/5} = \left[ (-32)^{4/5} \right]^3 = [-2]^4 = 16$

Case 3: $m$ is odd but $n$ is even. In this case, $x^{m/n}$ is undefined if $x < 0$ . For example, we would like $(-16)^{3/2}$ to be equal to $\left[ (-16)^{1/2} \right]^3$ , but ${-16}^{1/2} = \sqrt{-16}$ is undefined (using real numbers).

Case 4. $m$ and $latex $n$ are both even. This is perhaps the most interesting case. For example, how should we evaluate $(-8)^{4/6}$ ?. There are two legitimate choices… which lead to different answers!

Option #1: If we just apply the proposed definition of $x^{m/n}$ , we find that

$(-8)^{2/6} = \left[ (-8)^2 \right]^{1/6} = [64]^{1/6} = 2$

Option #2: We could first reduce $2/6$ to lowest terms:

$(-8)^{2/6} = (-8)^{1/3} = -2$

So… which is it?!?!?!?! The rule that mathematicians have chosen is that simplifying the exponent takes precedence over the above definition. In other words, the definition $x^{m/n} = \left[ x^{1/n} \right]^m$ should only be applied in $m/n$ has been reduced to lowest terms in order to remove the above ambiguity.

For the sake of completeness, I note that the above discussion restricts our attention to real numbers. If complex numbers are permitted, then things become a lot more interesting. If we repeat a few of the above calculations using complex numbers, we get answers that are different!

The explanation for this surprising result is not brief, but I discussed it in a previous series of posts:

https://meangreenmath.com/2014/06/19/calculators-and-complex-numbers-part-1/

https://meangreenmath.com/2014/06/20/calculators-and-complex-numbers-part-2/

https://meangreenmath.com/2014/06/21/calculators-and-complex-numbers-part-3/

https://meangreenmath.com/2014/06/22/calculators-and-complex-numbers-part-4/

https://meangreenmath.com/2014/06/23/calculators-and-complex-numbers-part-5/

https://meangreenmath.com/2014/06/24/calculators-and-complex-numbers-part-6/

https://meangreenmath.com/2014/06/25/calculators-and-complex-numbers-part-7/

https://meangreenmath.com/2014/06/26/calculators-and-complex-numbers-part-8/

https://meangreenmath.com/2014/06/27/calculators-and-complex-numbers-part-9/

https://meangreenmath.com/2014/06/28/calculators-and-complex-numbers-part-10/

https://meangreenmath.com/2014/06/29/calculators-and-complex-numbers-part-11/

https://meangreenmath.com/2014/06/30/calculators-and-complex-numbers-part-12/

https://meangreenmath.com/2014/07/01/calculators-and-complex-numbers-part-13/

https://meangreenmath.com/2014/07/02/calculators-and-complex-numbers-part-14/

https://meangreenmath.com/2014/07/03/calculators-and-complex-numbers-part-15-2/

https://meangreenmath.com/2014/07/04/calculators-and-complex-numbers-part-16/

https://meangreenmath.com/2014/07/05/calculators-and-complex-numbers-part-17/

https://meangreenmath.com/2014/07/06/calculators-and-complex-numbers-part-18/

https://meangreenmath.com/2014/07/07/calculators-and-complex-numbers-part-19/

https://meangreenmath.com/2014/07/08/calculators-and-complex-numbers-part-20/

https://meangreenmath.com/2014/07/09/calculators-and-complex-numbers-part-21/

https://meangreenmath.com/2014/07/10/calculators-and-complex-numbers-part-22/

https://meangreenmath.com/2014/07/11/calculators-and-complex-numbers-part-23/

https://meangreenmath.com/2014/07/12/calculators-and-complex-numbers-part-24/

Inverse Functions: nth Roots (Part 7)

In the previous posts of this series, I carefully considered the definition of $f(x) = \sqrt{x} = x^{1/2}$ . Let’s now repeat this logic to consider the definition of $f(x) = \sqrt[n]{x} = x^{1/n}$ , where $n \ge 3$ is an integer. We begin with $n$ even.

A typical case is $n =4$ ; the graph of $y = x^4$ is shown below.

The full graph of $y= x^n$ fails the horizontal line test if $n$ is even. Therefore, we need to apply the same logic that we used earlier to define $y = \sqrt[n]{x}$ . In particular, we essentially erase the left half of the graph. By restricting the domain to $[0,\infty)$ , we create a new function that does satisfy the horizontal line test, so that the graph of $y = \sqrt[n]{x}$ is found by reflecting through the line $y = x$ .

Written in sentence form,

If $n$ is even, then $y = \sqrt[n]{x}$ means that $x = y^n$ and $y \ge 0$ . In particular, this is impossible for real $y$ if $x < 0$ .

green line
We now turn to the case of $n$ odd. Unlike before, the full graph of $y= x^n$ (in thick blue) satisfies the horizontal line test. Therefore, there is no need to restrict the domain to define the inverse function. (shown in thin purple).

In other words,

If $n$ is odd, then $y = \sqrt[n]{x}$ means that $x = y^n$ . There is no need to give a caveat on the possible values of $y$ .

In particular, $\sqrt{-8}$ and $\sqrt[4]{-8}$ are both undefined since there is no (real) number $x$ so that $x^2 = -8$ or $x^4 = -8$ . However, $\sqrt[3]{-8}$ is defined and is equal to $-2$ since $(-2)^3 = -8$ .

Inverse Functions: Square Root (Part 6)

In this post, I take a deeper look at the standard mistake of “simplifying” $\sqrt{x^2}$ incorrectly as just $x$ .

In the previous post, we noted that the function $f: \mathbb{R} \to \mathbb{R}$ defined by $f(x) = x^2$ fails the horizontal line test and thus does not have an inverse function.

However, we can restrict the domain of $f$ to make a new function that does satisfy the horizontal line test. This new function is identical to $f$ where both $f$ and $g$ are defined. Following tradition, we restrict the domain to $[0,\infty)$ :

$g: [0,\infty) \to [0,\infty)$ defined by $g(x) = x^2$ .

So by essentially erasing the left half of the parabola, we form a function that passes the horizontal line test which therefore has an inverse. Naturally, this function is $g^{-1}(x) = \sqrt{x}$ . When I teach Precalculus, I like to write this as a sentence:

$y = \sqrt{x}$ means that $x = y^2$ and $y \ge 0$ .

Since $g$ and $g^{-1}$ are inverse functions, it’s always true that $g(g^{-1}(x)) = x$ and $g^{-1}(g(x)) = x$ whenever these functions are defined. For example,

$g(g^{-1}(16)) = g(\sqrt{16}) = g(4) = 4^2 = 16$ and

$g^{-1}(g(3)) = g^{-1}(3^2) = g^{-1}(9) = \sqrt{9} = 3$

In other words, we are guaranteed that $g^{-1}(g(x)) = g^{-1}(x^2) = \sqrt{x^2}$ is always equal to $x$ — as long $x$ lies in the domain of $g$ … or, in other words, as long as $x$ is nonnegative.

Because if $x$ is negative, all bets are off.

Remember, the original function $f$ does not have an inverse. In particular, $g^{-1}$ and $f$ are not inverse functions, and so it’s possible for $g^{-1}(f(x))$ to be something other than $x$ . For example,

$g^{-1}(f(3)) = \sqrt{3^2} = \sqrt{9} = 3$ , but

$g^{-1}(f(-3)) = \sqrt{(-3)^2} = \sqrt{9} = 3 \ne -3$

Of course, I don’t expect my Precalculus students to remember the subtle reason that this fails when they do their homework problems. But I do tell my Precalculus students that the nontrivial simplification of $\sqrt{x^2}$ is a natural consequence of restricting the domain of a function that does not pass the horizontal line test to define an inverse function. In this example, $\sqrt{x^2} = x$ as long as $x \ge 0$ . However, if $x < 0$ , then the result really could be just about anything else. For the current example, we have the pairwise simplification

$\sqrt{x^2} = x$ if $x \ge 0$ ;

$\sqrt{x^2} = -x$ if $x < 0$ .

The last line is often uncomfortable for students, and so I remind them that $x$ is assumed to be negative so that $-x$ is positive. Of course, there’s a new notation that mathematicians have developed so that this two-line simplification of $\sqrt{x^2}$ can be compressed to a single line:

$\sqrt{x^2} = |x|$

Unfortunately, in my opinion, this remains the problem that can be stated in two seconds or less (“Simplify the square root of $x$ squared”) that, in my opinion, is missed most often by mathematics students.

Inverse Functions: Restricted Domain for Square Root (Part 5)

With the last four posts as prelude, let’s consider finding the inverse of the function $f: \mathbb{R} \to \mathbb{R}$ defined by $f(x) = x^2$ .

So how will we find the inverse of $f$ ? Well, we can’t. But we can do something almost as good: we can define a new function $g$ that’s going look an awful lot like $f$ . Here’s the function:

$g: [0,\infty) \to [0,\infty)$ defined by $g(x) = x^2$ .

Notice that the function $g$ looks an awful lot like $f$ , except that the domain has been restricted. In this way, the left half of the graph of $f$ is essentially erased to produce the graph of $g$ .

So while the graph of $f$ fails the horizontal line test, the graph of $g$ does pass the horizontal line test. Therefore, $g$ has an inverse function. We reverse the roles of domain and range (of course, for this example, the domain and range are identical):

$g^{-1}: [0,\infty) \to [0,\infty)$

Also, the graph of $g^{-1}$ can be produced by reflecting through the line $y=x$ , producing the purple graph below.

Of course, the function $g^{-1}(x)$ is more customarily written as $\sqrt{x}$ . Stated another way using the restricted domain of $g$ .

$y = \sqrt{x}$ means that $x = y^2$ and $y \ge 0$ .

Pedagogically, when teaching Precalculus, I’ve found that this way of writing the definition of $\sqrt{x}$ is a useful prelude to the definition of the inverse trigonometric functions.

A couple of notes:

Notice that, if the purple parabola was completed, the full parabola would violate the vertical line test and thus fail to be a function. Thinking back to the original function, that’s another way of saying that the original full parabola violates the horizontal line test.
Since $g$ and $g^{-1}$ are inverse functions, it’s always true that $g(g^{-1}(x)) = x$ and $g^{-1}(g(x)) = x$ . However, $g^{-1}$ and $f$ are not inverse functions, and so it’s possible for $g^{-1}(f(x))$ to be something other than $x$ . This subtle distinction will be discussed more in tomorrow’s post.
Restricting the domain to $[0,\infty)$ was a perfectly arbitrary decision. It would have been perfectly OK if we have chosen the left half of the original parabola instead of the right half, as either half of the parabola satisfies the horizontal line test. So why did we choose the right half (with the nonnegative domain) instead of the left half (with the nonpositive domain)? That I can answer with one word: tradition. (By the way, finding an expression for the restriction of $f$ to $(-\infty,0])$ is a standard problem in a first course in real analysis.

Inverse Functions: Solving Equations (Part 4)

Although disguised, inverse functions play an important role in the ordinary solution of equations. For example, consider the steps used to solve this simple algebra problem:

$2x + 4 = 10$

$2x = 6$

$x = 3$

To go from the first equation to the second equation, let $X_1 = 2x+4$ and $X_2 = 10$ , and let $f(x) = x – 4$. This is an bijective function with inverse $f^{-1}(x) = x +4$ . Therefore,

$X_1 = X_2 \quad \Longleftrightarrow \quad f(X_1) = f(X_2)$

Stated another way,

$2x + 4 = 10 \quad \Longleftrightarrow 2x = 6$

Again, let $X_3 = 2x$ and $X_4 = 6$, and let $g(x) = x/2$. This is also a bijective function with inverse function $g^{-1}(x) = 2x$. Therefore,

$X_3= X_4 \quad \Longleftrightarrow \quad g(X_1) = g(X_2)$

Stated another way,

$latex 2x + 4 = 10 \quad \Longleftrightarrow 2x = 6 \quad \Longleftrightarrow x = 3$

So we are guaranteed that $x= 3$ is the one and only one solution of this equation.

If the process of solving an equation requires the use of a function that isn’t a bijection, then funny things can happen. For example, consider the slightly more complicated equation

$\sqrt{x} = x - 6$

Let’s starting solving by squaring both sides:

$x = (x-6)^2$

$x = x^2 - 12x + 36$

$0 = x^2 - 13x + 36$

$0 = (x-9)(x-4)$

$x - 9 = 0 \quad \hbox{or} \quad x - 4 = 0$

$x = 9 \quad \hbox{or} \quad x = 4$

So there are two solutions, right? Well…

$\sqrt{9} = 3 = 9 - 6$ ,

but $\sqrt{4} \ne 4 - 6$ !

So what happened? In other words, what is qualitatively different about this problem that didn’t happen in the first problem to produce an extraneous solution? The problem is the first step. Let $X_1 = \sqrt{x}$ and $X_2 = x-6$ . We applied the function $f(x) = x^2$ to both sides. Unfortuntely, $f(x) = x^2$ is not an invertible function when using the entire real line as the domain of $f$ . In other words,

$\sqrt{x} = x -6 \quad$ implies $\quad x = (x-6)^2$ ,

but $x =(x-6)^2 \quad$ does not imply that $\quad \sqrt{x} = x - 6$ .

The practical upshot is that, when arriving at the final step of the solution, we can’t be certain that the “solutions” we obtain actually work. Instead, what we’ve really shown that anything other than the solutions can’t work, which is different than saying that these two solutions actually do work. So it remains to actually check that these potential solutions are actually solutions (or not).

Inverse Functions: Definition and Horizontal Line Test (Part 3)

From MathWorld, a function $f: A \to B$ is an object $f$ such that every $a \in A$ is uniquely associated with an object $f(a) \in B$ . Stated more pedantically, if $a_1, a_2 \in A$ and $a_1 = a_2$ , then $f(a_1) = f(a_2)$ . More colloquially, in the graphs that ordinarily appear in secondary school, every $x-$ coordinate of the graph is associated with a unique $y-$ coordinate.

For this reason, the figure below (taken from http://en.wikipedia.org/wiki/Vertical_line_test) is not a function. The three points share a common $x-$ coordinate but have different $y-$ coordinates. In school, we usually teach students to distinguish functions from non-functions by the Vertical Line Test.

It is possible for a function to be a function but not have an inverse. Also from MathWorld, a function $f$ is said to be an injection (or, in the lingo that I learned as a student, one-to-one) if, whenever $f(x_1) = f(x_2)$ , it must be the case that $x_1=x_2$ . Equivalently, $x_1 \ne x_2$ implies $f(x_1) \ne f(x_2)$ . In other words, $f$ is an injection if it maps distinct objects to distinct objects.

The following image (taken from http://en.wikipedia.org/wiki/Horizontal_line_test) illustrates a function that is not injective (or, more accurately, is not injective when using all of the function’s domain). The horizontal line intersects the graph of the function at three distinct points with three different $x-$ intercepts which are associated with the same $y$ -coordinate.

By ensuring that the range of $f$ is restricted to the values that are actually attained by $f$ , the function $f$ may be considered as bijective and hence has an inverse function. The inverse function $f^{-1}$ is logically defined as

$f^{-1}(y) = x \quad \Longleftrightarrow \quad f(x) = y$

In this way, $f^{-1}(f(x)) = x$ and $f \left( f^{-1}(y) \right) = y$ for all $x$ in the domain of $f$ and all $y$ in the range of $f$ . Becaise $(x,y)$ is on the graph of $f$ if and only if $(y,x)$ is on the graph of $f^{-1}$ , the graph of $f^{-1}$ may be obtained by reflecting the graph of $y = f(x)$ through the line $y = x$ . Stated another way, to ensure that $f^{-1}$ is a function that satisfies the horizontal line test, it must be the case (when looking at the reflection through $y= x$ that the original function satisfies the horizontal line test.

Inverse functions: Square root (Part 2)

Here is one of the questions that I ask my class of future secondary mathematics teachers to answer.

A student asks, “My father was helping me with my homework last night and he said the book is wrong. He said that $\sqrt{4} = 2$ and $\sqrt{4} = -2$ , because $2^2 = 4$ and $(-2)^2 = 4$ . But the book says $\sqrt{4} = 2$ . He wants to know why we are using a book that has mistakes.”

This is a very similar question to the simplification of $\sqrt{x^2}$ , which was discussed in yesterday’s post. My experience has been that the above misconceptions involves confusion surrounding two very similar-sounding questions.

Question #1: Find all values of $x$ so that $x^2 = 9$ .

Question #2: Find the nonnegative value of $x$ so that $x^2 = 9$ .

The first question can be restated as solving $x^2-9 = 0$ , or finding all roots of a second-order polynomial. Accordingly, there are two answers. (Of course, the answers are $3$ and $-3$ , written more succinctly as $\pm 3$ .) The second question asks for the positive answer to Question #1. This positive answer is defined to be $\sqrt{9}$ , or $3$ .

In other words, it’s important to be sure that you’re answering the right question.

Is it all that important that $\sqrt{9}$ is chosen to be the nonnegative solution to Question #1? Not really. We could have easily chosen the negative answer. The reason we choose the positive answer and not the negative answer can be answered in one word: tradition.

We want $f(x) = \sqrt{x}$ to be a well-defined function that produces only one output value, and there’s no mathematically advantageous reason for choosing the nonnegative answer aside from the important consideration that everyone else does it that way. And though students probably won’t remember this tidbit of wisdom when the time comes, the same logic applies when choosing the range of the inverse trigonometric functions.

Of course, for the present case, it totally makes sense to take the positive, less complicated answer as the output of $\sqrt{x}$ . However, this won’t be as readily apparent when we consider the inverse trigonometric functions.