Different definitions of logarithm: Index

I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on how the different definitions of logarithm are in fact equivalent.

Part 1: Introduction to the two definitions: an antiderivative and an inverse function.

Part 2: The main theorem: four statements only satisfied by the logarithmic function.

Part 3: Case 1 of the proof: positive integers.

Part 4: Case 2 of the proof: positive rational numbers.

Part 5: Case 3 of the proof: negative rational numbers.

Part 6: Case 4 of the proof: irrational numbers.

Part 7: Showing that the function $f(x) = \displaystyle \int_1^x \frac{dt}{t}$ satisfies the four statements.

Part 8: Computation of standard integrals and derivatives involving logarithmic and exponential functions.

Calculators and Complex Numbers: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on how the trigonometric form of complex numbers, DeMoivre’s Theorem, and extending the definitions of exponentiation and logarithm to complex numbers.

Part 1: Introduction: using a calculator to find surprising answers for $\ln(-5)$ and $\sqrt[3]{-8}$ . See the video below.

Part 2: The trigonometric form of complex numbers.

Part 3: Proving the theorem

$\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$

Part 4: Proving the theorem

$\displaystyle \frac{ r_1 (\cos \theta_1 + i \sin \theta_1) }{ r_2 (\cos \theta_2 + i \sin \theta_2) } = \displaystyle \frac{r_1}{r_2} (\cos [\theta_1-\theta_2] + i \sin [\theta_1-\theta_2])$

Part 5: Application: numerical example of De Moivre’s Theorem.

Part 6: Proof of De Moivre’s Theorem for nonnegative exponents.

Part 7: Proof of De Moivre’s Theorem for negative exponents.

Part 8: Finding the three cube roots of -27 without De Moivre’s Theorem.

Part 9: Finding the three cube roots of -27 with De Moivre’s Theorem.

Part 10: Pedagogical thoughts on De Moivre’s Theorem.

Part 11: Defining 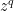$z^q$ for rational numbers $q$ .

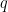Part 12: The Laws of Exponents for complex bases but rational exponents.

Part 13: Defining $e^z$ for complex numbers $z$

Part 14: Informal justification of the formula 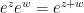$e^z e^w = e^{z+w}$ .

Part 15: Simplification of 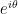$e^{i \theta}$ .

Part 16: Remembering DeMoivre’s Theorem using the notation 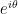$e^{i \theta}$ .

Part 17: Formal proof of the formula 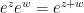$e^z e^w = e^{z+w}$ .

Part 18: Practical computation of $e^z$ for complex $z$ .

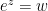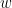Part 19: Solving equations of the form $e^z = w$ , where $z$ and $w$ may be complex.

Part 20: Defining 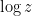$\log z$ for complex $z$ .

Part 21: The Laws of Logarithms for complex numbers.

Part 22: Defining $z^w$ for complex $z$ and $w$ .

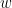Part 23: The Laws of Exponents for complex bases and exponents.

Part 24: The Laws of Exponents for complex bases and exponents.

Two ways of doing an integral: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on different ways of computing the integral $\displaystyle \int \frac{dx}{\sqrt{4x-x^2}}$ .

Part 1: The two “different” answers.

Part 2: Explaining why the two “different” answers are really equivalent.

Correlation and Causation: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on data sets that (hopefully) persuade students that correlation is not the same as causation.

Part 1: Piracy and global warming. Also, usage of Internet Explorer and murder.

Part 2: An xkcd comic.

Part 3: STEM spending and suicide. Consumption of margarine and divorce. Consumption of mozzarella and earning a doctorate. Marriage rates and deaths by drowning.

Day One of My Calculus Class: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on what I teach my students on the first day of calculus in order to start the transition from Precalculus and to get them engaged for what we’ll be doing throughout the semester.

Part 1: The two themes of calculus: Approximating curved things by straight things and passing to limits.

Part 2: Using the distance-rate-time formula to estimate how fast an accelerating object lands when dropped from a tall building.

Part 3: Passing to limits to precisely calculate the above velocity.

Part 4: Using rectangles to estimate the area under a parabola.

Part 5: Passing to limits to precisely calculate the area under a parabola.

Part 6: Final comments: these two questions apparently have nothing to do with each other, but are in fact highly interrelated. The connection between these two topics, the Fundamental Theorem of Calculus, is one of greatest discoveries in the history of mankind, which my students are now privileged to understand at the ripe old age of 18 or 19 years old.

Fun lecture on geometric series: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series concerning one of my favorite lectures concerning various applications of geometric series.

Part 1: Introduction to generating functions.

Part 2: Enumeration problems; or counting how many ways $2.00 can be formed using pennies, nickels, dimes, and quarters. (The answer is 1463.)

Part 3: The generating function for the Fibonacci sequence.

Part 4: Using a generating function to find a closed-form expression for the (ahem) Quintanilla sequence, a close but somewhat less famous relative of the Fibonacci sequence.

Part 5: Reproving the formula for the Quintanilla sequence using mathematical induction.

Thoughts on 1/7 and Other Rational Numbers: Index

Part 1: A way to remember the decimal expansion of $\displaystyle \frac{1}{7}$ .

Part 2: Long division and knowing for certain that digits will start repeating.

Part 3: Converting a repeating decimal into a fraction, using algebra.

Part 4: Converting a repeating decimal into a fraction, using infinite series.

Part 5: Quickly converting fractions of the form $\displaystyle \frac{M}{10^t}$ , $\displaystyle \frac{M}{10^k-1}$ , and $\displaystyle \frac{M}{10^t (10^k-1)}$ into decimals without using a calculator.

Part 6: Converting any rational number into one of the above three forms, and then converting into a decimal.

Part 7: Same as above, except using a binary (base-2) expansion instead of a decimal expansion.

Part 8: Why group theory relates to the length of the repeating block in a decimal expansion.

Part 9: A summary of the above ideas to find the full decimal expansion of $\displaystyle \frac{8}{17}$ , which has a repeating block longer than the capacity of most calculators.

Part 10: More thoughts on $\displaystyle \frac{8}{17}$ .

Calculator Errors: When Close Isn’t Close Enough (Index)

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on how I remind students about Taylor series. I often use this series in a class like Differential Equations, when Taylor series are needed but my class has simply forgotten about what a Taylor series is and why it’s important.

Part 1: Propagation of small numerical errors.

Part 2: A tragedy during the 1991 Gulf War that was a direct result of calculator rounding.

Square roots and Logarithms Without a Calculator: Index

Part 1: Method #1: Trial and error.

Part 2: Method #2: An algorithm comparable to long division.

Part 3: Method #3: Introduction to logarithmic tables. At the time of this writing, this is the most viewed page on my blog.

Part 4: Finding antilogarithms with a table.

Part 5: Pedagogical and historical thoughts on log tables.

Part 6: Computation of square roots using a log table.

Part 7: Method #4: Slide rules

Part 8: Method #5: By hand, using a couple of known logarithms base 10, the change of base formula, and the Taylor approximation $ln(1+x) \approx x$ .

Part 9: An in-class activity for getting students comfortable with logarithms when seen for the first time.

Part 10: Method #6: Mentally… anecdotes from Nobel Prize-winning physicist Richard P. Feynman and me.

Part 11: Method #7: Newton’s Method.

Why does x^0 = 1 and x^(-n) = 1/x^n? (Index)

Part 1: Multiplication and division.

Part 2: The Laws of Exponents.