The number of digits in n! (Part 3)

The following graph shows the number of digits in $n!$ as a function of $n$ .

When I was in school, I stared at this graph for weeks, if not months, trying to figure out an equation that would fit these points. And I never could figure it out.

When I took calculus in college, I distinctly remember getting up the nerve to ask my professor, the great L.Craig Evans (now at UC Berkeley), if he knew how to solve this problem. To my great consternation, he immediately wrote down what I now realize to be the right answer, using Stirling’s approximation:

$\ln n! \approx \left(n + \displaystyle \frac{1}{2} \right) \ln n - n + \frac{1}{2} \ln (2\pi)$

While I now know that this was the way to go about solving this problem, I didn’t appreciate how this formula could help me at the time. I only saw the $n!$ on the left-hand side and did not see the immediate connection between this formula and the number of digits in $n!$ .

But now I know better.

For starters, the number of base-10 digits in a number $n$ is always the next integer greater that $\log_{10} n$ . For example, $\log_{10} 2000 \approx 3.301$, and the next integer larger than $3.301$ is 4. Unsurprisingly, the number $2000$ has 4 digits.

Second, the change of base formula for logarithms gives

$\log_{10} n! = \displaystyle \frac{\ln n!}{\ln 10}$

Therefore, the number of digits in $n!$ will be about

$\displaystyle \frac{\left(n + \displaystyle \frac{1}{2} \right) \ln n - n + \frac{1}{2} \ln (2\pi)}{\ln 10}$

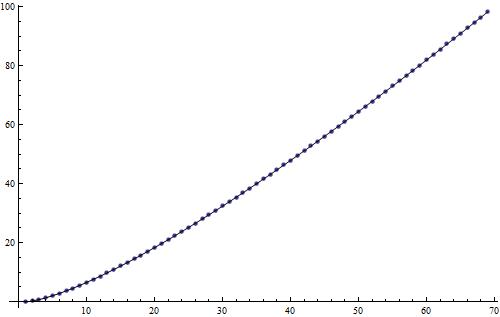
The graph below shows just how accurate this approximation really is. The solid curve is the approximation; the dots are the values of $\log_{10} n!$ . (In other words, this series of dots are only slightly different than the dots above, which have integers as coordinates.) Not bad at all… the error in the approximation is smaller than the size of the dots in this picture.

The number of digits in n! (Part 2)

The following graph shows the number of digits in $n!$ as a function of $n$ .

When I was in school, I stared at this graph for weeks, if not months, trying to figure out an equation that would fit these points. And I never could figure it out.

In retrospect, my biggest mistake was thinking that the formula had to be something like $y = a x^m$ , where the exponent $m$ was a little larger than 1. After all, the graph is clearly not a straight line, but it’s also not as curved as a parabola.

What I didn’t know then, but know now, is that there’s a really easy way to determine to determine if a data set exhibits power-law behavior. If $y = a x^m$ , then

$\ln y = \ln a + m \ln x$ .

If we make the substitutions $Y = \ln Y$ , $B = \ln a$ , and $X = \ln x$ , then this equation becomes

$Y = m X + B$

In other words, if the data exhibits power-law behavior, then the log-transformed data would look very much like a straight line. Well, here’s the graph of $(X,Y)$ after applying the transformation:

Ignoring the first couple of pots, the dots show an ever-so-slight concave down pattern, but not enough that would have discouraged me from blindly trying a pattern like $y = a x^m$ . However, because these points do not lie on a straight line and exhibit heteroscedastic behavior, my adolescent self was doomed to failure.

The number of digits in n! (Part 1)

When I was in school, perhaps my favorite pet project was trying to find a formula for the number of digits in $n!$ . For starters:

$0! = 1$ : 1 digit
$1! = 1$ : 1 digit
$2! = 2$ : 1 digit
$3! = 6$ : 1 digit
$4! = 24$ : 2 digits
$5! = 120$ : 3 digits
$6! =720$ : 3 digits
$7! = 5040$ : 4 digits
$8! = 40,320$ : 5 digits

I owned what was then a top-of-the-line scientific calculator (with approximately the same computational capability as a modern TI-30), and I distinctly remember making a graph like the following on graph paper. The above calculations contribute the points $(0,1)$ , $(1,1)$ , $(2,1)$ , $(3,1)$ , $(4,2)$ , $(5,3)$ , $(6,3)$ , $(7,4)$ , and $(8,5)$ .

I had to stop (or, more accurately, I thought I had to stop) at $69!$ because my calculator couldn’t handle numbers larger than $10^{100}$ .

I stared at this graph for weeks, if not months, trying to figure out an equation that would fit these points. And I never could figure it out.

And, to this day, I’m somewhat annoyed at my adolescent self that I wasn’t able to figure out this puzzle for myself… since I had all the tools in my possession needed to solve the puzzle, though I didn’t know how to use the tools.

In this series of posts, I’ll answer this question with the clever application of some concepts from calculus and precalculus.

Proof without words: The difference of consecutive cubes

Source: https://www.facebook.com/photo.php?fbid=451328078334029&set=a.416585131808324.1073741827.416199381846899&type=1&theater

For a more conventional algebraic proof, notice that

$(n+1)^3 - n^3 = n^3 + 3n^2 + 3n + 1 - n^3 = 3n(n+1) + 1$

The product $n(n+1)$ is always an even number times an odd number: if $n$ is even, then $n+1$ is odd, but if $n$ is odd, then $n(n+1)$ . So $n(n+1)$ is a multiple of 2, and so $3n(n+1)$ is a multiple of 6. Therefore, $3n(n+1)+1$ is one more than a multiple of 6, proving the theorem.

Compound Interest and Mary Poppins

What would have happened if Michael Banks had invested his tuppence in a savings account? FiveThirtyEight has the answer.

Square roots and Logarithms Without a Calculator: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on computing square roots and logarithms without a calculator.

Part 1: Method #1: Trial and error.

Part 2: Method #2: An algorithm comparable to long division.

Part 3: Method #3: Introduction to logarithmic tables. At the time of this writing, this is the most viewed page on my blog.

Part 4: Finding antilogarithms with a table.

Part 5: Pedagogical and historical thoughts on log tables.

Part 6: Computation of square roots using a log table.

Part 7: Method #4: Slide rules

Part 8: Method #5: By hand, using a couple of known logarithms base 10, the change of base formula, and the Taylor approximation $ln(1+x) \approx x$ .

Part 9: An in-class activity for getting students comfortable with logarithms when seen for the first time.

Part 10: Method #6: Mentally… anecdotes from Nobel Prize-winning physicist Richard P. Feynman and me.

Part 11: Method #7: Newton’s Method.

Why does x^0 = 1 and x^(-n) = 1/x^n? (Index)

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series why the rules for $x^0$ and $x^{-n}$ work the way they do.

Part 1: Multiplication and division.

Part 2: The Laws of Exponents.

Why does 0! = 1? (Index)

Part 1: Multiplication and division.

Part 2: Combinatorics.

A Curious Square Root: Index

I’m using the Twelve Days of Christmas (and perhaps a few extra days besides) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on expressions containing nested square roots that nevertheless can be simplified.

Part 1: Simplifying $\sqrt{5 - \sqrt{6} + \sqrt{22+8\sqrt{6}}}$ .

Part 2: DIfferent ways of calculating $\sin 15^\circ$ .

2048 and algebra: Index

I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on using algebra to study the 2048 game… with a special focus on reaching the event horizon of 2048 which cannot be surpassed.

2048-0 Part 1: Introduction and statement of problem

Part 2: First insight: How points are accumulated in 2048

Part 3: Second insight: The sum of the tiles on the board

Part 4: Algebraic formulation of the two insights

Part 5: Algebraic formulation applied to a more complicated board

Part 6: Algebraic formulation applied to the event horizon of 2048

Part 7: Calculating one of the complicated sums in Part 6 using a finite geometric series

Part 8: Calculating another complicated sum in Part 6 using a finite geometric series

Part 9: Repeating Part 8 by reversing the order of summation in a double sum

Part 10: Estimating the probability of reaching the event horizon in game mode