Proofs Without Words: Alternating Sums of Consecutive Squares

For a visual proof that

$(2n)^2 - (2n+1)^2 + (2n+2)^2 \dots + (4n)^2 = -(4n+1)^2 + (4n+2)^2 \dots + (6n)^2$ ,

see https://www.facebook.com/photo.php?fbid=435352806598223&set=a.416585131808324.1073741827.416199381846899&type=1&theater.

Non-geometric infinite series (Part 12)

I conclude this series of posts with thoughts about infinite series which use reciprocals of positive integers. I offer this post for the enrichment of talented Precalculus students who have exhibited mastery of geometric series.

Geometric. As we’ve discussed at length, the series

$1 + \displaystyle \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots$

converges and is in fact equal to $2$ .

Harmonic. Including the reciprocals of all positive integers is called a harmonic series:

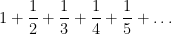
$1 + \displaystyle \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \dots$

As shown in the link to the MathWorld website, this series actually diverges, even though the terms get smaller and smaller.

So we’ve made an observation: if too many reciprocals are included, the series diverges. But if we take enough of them away, then we can still end up with a series that is infinite but converges.

Squares. Let’s now consider the reciprocals of perfect squares:

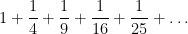
$1 + \displaystyle \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \dots$

Clearly, we’ve taken away a lot of the terms of the harmonic series? Have we taken enough away so that the series converges? It turns out that the answer is yes. And the answer is precisely what you’d think it should be (not): $\pi^2/6$ . This is just another way that the circumference of a circle has an odd way of appearing in the most unexpected of places.

The proof that this series equals $\pi^2/6$ requires the clever use of Parseval’s theorem from Fourier analysis.

Fourth Powers. Let’s now turn to the reciprocals of fourth powers:

$1 + \displaystyle \frac{1}{16} + \frac{1}{81} + \frac{1}{256} + \frac{1}{625} + \dots$

By the Direct Comparison Test and the series for reciprocals of squares, this series converges. Using Parseval’s theorem, it can be shown that the answer is 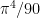$\pi^4/90$ .

Cubes. Now let’s investigate the reciprocals of cubes:

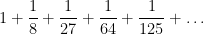
$1 + \displaystyle \frac{1}{8} + \frac{1}{27} + \frac{1}{64} + \frac{1}{125} + \dots$

Again by the Direct Comparison Test and the series for reciprocals for squares, this series must converge. This sum is called Apéry’s constant. However, and amazingly, no one knows what the answer is. Of course, a computer can be programmed to evaluate this series to as many decimal places as desired. According to Wikipedia, this sum was evaluated to over 100 billion decimal places in 2010. 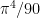However, to the best of my knowledge, no one has figured out if there’s a simple way of writing the answer, like $\pi^2/6$ or $\pi^4/90$ .

So if you figure out a simple way to evaluate Apéry’s constant, feel free to call me collect.

The previous four series are example of Riemann’s zeta function, which is of central importance in number theory and is the focus of the celebrated Riemann Hypothesis, for which a solution is worth a cool $1 million.

Primes. Now let’s consider the reciprocals of primes:

$\displaystyle \frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \dots$

As noted above, the harmonic series diverges, but if we remove enough terms from the harmonic series, then it’s possible to make an infinite series that converges. So the central question is, did we remove enough fractions (by taking away all of the composite denominators) so that the series converges?

Surprisingly, the answer is no: the sum of the reciprocals of the primes actually diverges. The proof actually requires a graduate-level class in analytic number theory.

By no means would I expect high school students to master all of the above facts. As noted above, the subject of this post is mostly for the enrichment of high school students who have mastered infinite geometric series.

That said, students who know the following facts from Precalculus will be well-served when they reach calculus and other university-level mathematics courses.

They should either know the formula for an infinite geometric series or else be able to quickly derive it.
They should know that not every infinite geometric series is geometric.
They should know that not every infinite series converges.
They should be familiar with the meaning of the terms converge and diverge.

Formula for an infinite geometric series (Part 11)

Many math majors don’t have immediate recall of the formula for an infinite geometric series. They often can remember that there is a formula, but they can’t recollect the details. While it’s I think it’s OK that they don’t have the formula memorized, I think is a real shame that they’re also unaware of where the formula comes from and hence are unable to rederive the formula if they’ve forgotten it.

In this post, I’d like to give some thoughts about why the formula for an infinite geometric series is important for other areas of mathematics besides Precalculus. (There may be others, but here’s what I can think of in one sitting.)

1. An infinite geometric series is actually a special case of a Taylor series. (See https://meangreenmath.com/2013/07/05/reminding-students-about-taylor-series-part-5/ for details.) Therefore, it would be wonderful if students learning Taylor series in Calculus II could be able to relate the new topic (Taylor series) to their previous knowledge (infinite geometric series) which they had already seen in Precalculus.

2. An infinite geometric series is also a special case of the binomial series $(1+x)^n$ , when $n$ does not have to be a positive integer and hence Pascal’s triangle cannot be used to find the expansion.

3. Infinite geometric series is a rare case when an infinite sum can be found exactly. In Calculus II, a whole battery of tests (e.g., the Root Test, the Ratio Test, the Limit Comparison Test) are introduced to determine whether a series converges or not. In other words, these tests only determine if an answer exists, without determining what the answer actually is.

Throughout the entire undergraduate curriculum, I’m aware of only four types of series that can actually be evaluated exactly.

An infinite geometric series with $-1 < r < 1$
The Taylor series of a real analytic function. (Of course, an infinite geometric series is a special case of a Taylor series.)
A telescoping series. For example, using partial fractions and cancelling a bunch of terms, we find that

$\displaystyle \sum_{k=1}^\infty \frac{1}{k^2+k} = \displaystyle \sum_{k=1}^\infty \left( \frac{1}{k} - \frac{1}{k+1} \right)$

$\displaystyle \sum_{k=1}^\infty \frac{1}{k^2+k} = \displaystyle \left( 1 - \frac{1}{2} \right) + \left( \frac{1}{2} - \frac{1}{3} \right) \dots$

$\displaystyle \sum_{k=1}^\infty \frac{1}{k^2+k} = 1$

An infinite series that arises from Parseval’s theorem in Fourier analysis.

4. Infinite geometric series are essential for proving basic facts about decimal representations that we often take for granted.

We can justify why $0.\overline{9} = 1$ . See https://meangreenmath.com/2013/09/03/why-does-0-999-1-part-3/ for details.
Along with the Direct Comparison Test, we can be used to justify why a decimal representation $0.d_1d_2d_3\dots$ actually converges and must correspond to a real number. See https://meangreenmath.com/2013/09/01/why-does-0-999-1-part-1/ for details.
We can prove that a fraction of the form $\displaystyle \frac{M}{10^k-1}$ must have a repeating block of length $k$ which contains the digits of $M$ . See https://meangreenmath.com/2013/08/22/thoughts-on-17-and-other-rational-numbers-part-5/ for details.
Going the other direction, we can also convert an repeating decimal representation into a fraction. See https://meangreenmath.com/2013/08/21/thoughts-on-17-and-other-rational-numbers-part-4/ for details.
We can also find representations in other bases besides base 10. See https://meangreenmath.com/2013/08/17/calculator-errors-when-close-isnt-close-enough-part-2 for an example of a repeating binary representation.

5. Properties of an infinite geometric series are needed to find the mean and standard deviation of a geometric random variable, which is used to predict the number of independent trials needed before an event happens. This is used for analyzing the coupon collector’s problem, among other applications.

Formula for an arithmetic series (Part 7)

As we’ve discussed, the formula for an arithmetic series is

$S_n = \displaystyle \frac{n}{2} (2a_1 + [n-1] d) = \displaystyle \frac{n}{2} (a_1 + a_n)$ ,

where $n$ is the number of terms, $a_1$ is the first term, $d$ is the common difference, and $a_n$ is the last term. This formula may be more formally expressed as

$S = \displaystyle \sum_{k=1}^n a_k = \displaystyle \frac{n}{2} (2a_1 + [n-1] d) = \displaystyle \frac{n}{2} (a_1 + a_n)$

For homework and on tests, students are asked to directly plug into this formula and to apply this problem with word problems, like finding the total number of seats in an auditorium with 50 rows, where there are 12 seats in the front row and each row has two more seats than the row in front of it.

In my opinion, the ability to solve questions like the one below is the acid test for determining whether a student — who I assume can solve routine word problems like the one above — really understands series or is just familiar with series. In other words, if a student can solve routine word problems but is unable to handle a problem like the one below, then there’s still room for that student’s knowledge of series to deepen.

Calculate $\displaystyle \sum_{k=11}^{60} (5k - 2)$

There are two reasonable approaches for solving this problem.

Solution #1. Notice that $5k - 2 = 5(k-1) + 5 - 2 = 3 + 5(k-1)$ . So this is really an arithmetic series whose first term is $3$ and whose common difference is $5$ . Therefore,

$S = \displaystyle \sum_{k=1}^{60} a_k = \displaystyle \frac{60}{2} (2[3] + [60-1] 5)=9030$

However, I’m supposed to start the series on $k=11$ , not $k=1$ . That means that I need to subtract off the first ten terms of the above series. Now

$S = \displaystyle \sum_{k=1}^{10} a_k = \displaystyle \frac{10}{2} (2[3] + [10-1] 5)= 255$

Finally,

$\displaystyle \sum_{k=11}^{60} a_k = \displaystyle \sum_{k=1}^{60} a_k - \displaystyle \sum_{k=1}^{10} a_k = 9030 - 255 = 8775$

Solution #2. Writing out the terms, we see that

$\displaystyle \sum_{k=11}^{60} (5k - 2) = (5[11]-2) + (5[12]-2) + \dots + (5[60]-2)$

$\displaystyle \sum_{k=11}^{60} (5k - 2) = 53+58 + \dots +298$

The right-hand side is an arithmetic series whose “first” term is $53$ and whose last ( $50$ th) term is $298$ . Therefore,

$\displaystyle \sum_{k=11}^{60} (5k - 2) = \frac{50}{2} (53+298) = 8775$

Of the two solutions, I suppose I have a mild preference for the first, as the second solution won’t work for something like $\displaystyle \sum_{k=11}^{60} k^2$ . However, both solution demonstrate that the student is actually thinking about the meaning of the series instead of just plugging numbers in a formula, and so I’d be happy with either one in a Precalculus class.

Formula for an arithmetic series (Part 6)

In the previous posts of this series, I described two methods of deriving the formula

$\displaystyle \sum_{k=1}^n k = \frac{n(n+1)}{2}$

The first method concerned reversing the terms of the sum (or, almost equivalently, taking the terms in pairs). The second method used mathematical induction.

Mathematical induction can be applied to arithmetic series as well as other series. However, the catch is that you have to know the answer before proving that the answer actually is correct. By contrast, the first method did not require us to know the answer in advance — it just fell out of the calculation — but it cannot be applied to series that are not arithmetic.

Here’s a third method using the principle of telescoping series. This method has the strengths of the previous two methods: it does not require us to know the answer in advance, and it can also be applied to some other series which are not arithmetic.

To begin, consider the sum

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2]$

At this early point, students often object, “Where did that come from?” I’ve said it before but I’ll say it again: I tell them my usual tongue-in-cheek story that this idea comes from the patented Bag of Tricks. Socrates gave the Bag of Tricks to Plato, Plato gave it to Aristotle, it passed down the generations, my teacher taught the Bag of Tricks to me, and I teach it to my students.

In any event, I will evaluate this sum in two different ways.

Step 1. Just write out the terms of the series, starting from $k=1$ and ending with $k =n$ .

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = [1^2 - 0^2] + [2^2 - 1^2] + [3^2 - 2^2] + \dots + [n^2 - (n-1)^2]$

Notice that, on the right-hand side, the $1^2$ terms cancel, the $2^2$ terms cancel, and so on. In fact, almost everything cancels. The only two terms that aren’t cancelled are the $0^2$ and $n^2$ terms. Therefore,

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = n^2 - 0^2 = n^2$

Step 2. Next, we’ll rewrite the original sum by expanding out the terms inside of the sum:

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = \displaystyle \sum_{k=1}^n [k^2 - (k^2 -2k + 1)]$

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = \displaystyle \sum_{k=1}^n [2k-1]$

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = \displaystyle \sum_{k=1}^n 2k - \displaystyle \sum_{k=1}^n 1$

$\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = 2\displaystyle \sum_{k=1}^n k - \displaystyle \sum_{k=1}^n 1$

Step 3. Of course, these different looking answers from Steps 1 and 2 have to be the same, so let’s set them equal to each other:

$2\displaystyle \sum_{k=1}^n k - \displaystyle \sum_{k=1}^n 1 = n^2$

There is one unknown in this equation, $\displaystyle \sum_{k=1}^n k$ . The second sum is just the constant $1$ added to itself $n$ times, and so $\displaystyle \sum_{k=1}^n 1 = n$ . Therefore, we solve for the unknown: