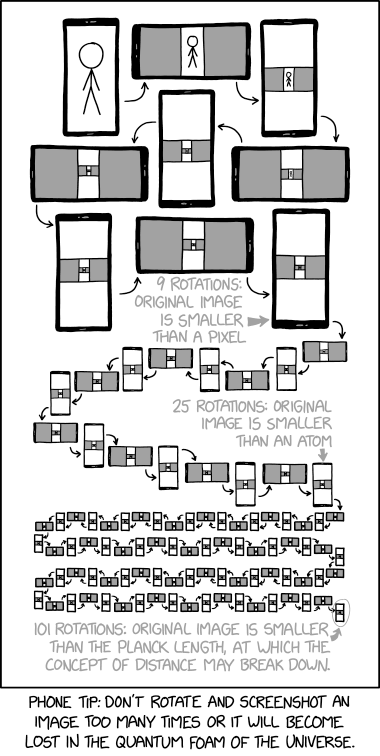
Source: https://xkcd.com/2671/

Source: https://xkcd.com/2671/
The proofs of Kepler’s Three Laws are usually included in textbooks for multivariable calculus. So I was very intrigued when I saw, in the Media Reviews of College Mathematics Journal, that somebody had published a proof of Kepler’s First Law that only uses algebra and trigonometry. Let me quote from the review:
Kepler’s first law states that bounded planetary orbits are elliptical. This law is presented in introductory textbooks, but the proof typically requires intricate integrals or vector analysis involving an accidental degeneracy. Simha offers an elementary proof of Kepler’s first law using algebra and trigonometry at the high school level.
https://doi.org/10.1080/07468342.2022.2026089
Once upon a time, I taught Precalculus for precocious high school students. I wish I had known of this result back then, as it would have been a wonderful capstone to their studies of trigonometry and the conic sections.
The preprint of this result can be found on arXiv. (The proof only addresses Kepler’s First Law and not the Second and Third Laws.) The actual article, for those with institutional access, was published in American Journal of Physics Vol. 89 No. 11 (2021): 1009-1011.

Source: https://xkcd.com/2687/
I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on computing square roots and logarithms without a calculator (with the latest post added).
Part 1: Method #1: Trial and error.
Part 2: Method #2: An algorithm comparable to long division.
Part 3: Method #3: Introduction to logarithmic tables.
Part 4: Finding antilogarithms with a table.
Part 5: Pedagogical and historical thoughts on log tables.
Part 6: Computation of square roots using a log table.
Part 7: Method #4: Slide rules
Part 8: Method #5: By hand, using a couple of known logarithms base 10, the change of base formula, and the Taylor approximation .
Part 9: An in-class activity for getting students comfortable with logarithms when seen for the first time.
Part 10: Method #6: Mentally… anecdotes from Nobel Prize-winning physicist Richard P. Feynman and me.
Part 11: Method #7: Newton’s Method.
Part 12: Method #8: The formula
When I was in middle school, I remember my teacher telling me, after I learned the quadratic formula, that there was a general formula for solving cubic and quartic equations, but no such formula existed for solving the quintic. This was also when I first heard the infamous story of young Galois’s death from a duel.
Using my profound middle-school logic, I took this story as a challenge to devise my own formula for solving the quintic. Naturally, my efforts came up short.
When I was in high school, with this obsession still fully intact, I attempted to read through the wonderful monograph Field Theory and Its Classical Problems. Here’s the MAA review of this book:
Hadlock’s book sports one of the best prefaces I’ve ever read in a mathematics book. The rest of the book is even better: in 1984 it won the first MAA Edwin Beckenbach Book Prize for excellence in mathematical exposition.
Hadlock says in the preface that he wrote the book for himself, as a personal path through Galois theory as motivated by the three classical Greek geometric construction problems (doubling the cube, trisecting angles, and squaring the circle — all with just ruler and compass) and the classical problem of solving equations by radicals. Unlike what happens in most books on the subject, all three Greek problems are solved in the first chapter, with just the definition of field as a subfield of the real numbers, but without even defining degree of field extensions, much less proving its multiplicativity (this is done in chapter 2). Doubling the cube is proved to be impossible by proving that the cube root of 2 cannot be an element of a tower of quadratic extensions: if the cube root of 2 is in a quadratic extension, then it is actually in the base field. Repeating the argument, we conclude that it is not constructible because it is not rational. A similar argument works for proving that trisecting a 60 degree angle is impossible. Of course, proving that duplicating the cube is impossible needs a different argument: chapter 1 ends with Niven’s proof of the transcendence of π.
After this successful bare-hands attack at three important problems, Chapter 2 discusses in detail the construction of regular polygons and explains Gauss’s characterization of constructible regular polygons, including the construction of the regular 17-gon. Chapter 3 describes Galois theory and the solution of equations by radicals, including Abel’s theorem on the impossibility of solutions by radicals for equations of degree 5 or higher. Chapter 4, the last one, considers a special case of the inverse Galois problem and proves that there are polynomials with rational coefficients whose Galois group is the symmetric group, a result that is established via Hilbert’s irreducibility theorem.
Many examples, references, exercises, and complete solutions (taking up a third of the book!) are included and make this enjoyable book both an inspiration for teachers and a useful source for independent study or supplementary reading by students.
As I recall, I made it successfully through the first couple of chapters but started to get lost with the Galois theory somewhere in the middle of Chapter 3. Despite not completing the book, this was one of the most rewarding challenges of my young mathematical life. Perhaps one of these days I’ll undertake this challenge again.
Anyway, this year I came across the wonderful article The Abel–Ruffini Theorem: Complex but Not Complicated in the March issue of the American Mathematical Monthly. The article presents a completely different way of approaching the insolvability of the quintic that avoids Galois theory altogether.
The proof is elementary; I’m confident that I could have understood this proof had I seen it when I was in high school. That said, the word “elementary” in mathematics can be a bit loaded — this means that it is based on simple ideas that are perhaps used in a profound and surprising way. Perhaps my favorite quote along these lines was this understated gem from the book Three Pearls of Number Theory after the conclusion of a very complicated proof in Chapter 1:
You see how complicated an entirely elementary construction can sometimes be. And yet this is not an extreme case; in the next chapter you will encounter just as elementary a construction which is considerably more complicated.
I believe that a paid subscription to the Monthly is required to view the above link, but the main ideas of the proof can be found in the video below as well as this short PDF file by Leo Goldmakher.
In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.
I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).
This student submission comes from my former student Emma White. Her topic, from Precalculus: finding the equation of a circle.
How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?
Ironically, this morning on the way to class I received a notification saying Coldplay dropped a new album called “ Music of the Spheres” and I couldn’t help but look into it more! Although we are talking about circles, as mathematicians (or other people who came across this blog), we realize that circles and spheres are related in some ways. Although that is a discussion for another time, I want to focus on this album and how it relates to our world. Circles are used in various ways when it comes to the “circle of life” or “time on a ticking clock”. One song talks about “Humankind” and how we’re designed. This is a continuous cycle as humans pass away and are born and the cycle continues. While this may be a more serious thing to think about, life happens and cycles (we also see this in history and cycles of conflicts, wars, and much more). Furthermore (and maybe on a more lighthearted feel), we see the concept of circle in “The Circle of Life” as seen in “The Lion King”. I encourage you to look at the lyrics below:
“From the day we arrive on the planet
And, blinking, step into the sun
There’s more to see than can ever be seen
More to do than can ever be done
There’s far too much to take in here
More to find than can ever be found
But the sun rolling high
Through the sapphire sky
Keeps great and small on the endless round
It’s the circle of life
And it moves us all
Through despair and hope
Through faith and love
‘Til we find our place
On the path unwinding
In the circle
The circle of life.”
Source: LyricFind
Songwriters: Elton John / Tim Rice
Circle of Life lyrics © Walt Disney Music Company
Whatever your background may be, we can agree that much in life happens in cycles (think of cells as well!) and that is done in a metaphorical circular motion. The moon rotates around the sun, the planets rotate around the sun, and so forth. Many songs capture the concept of “circling” or time (think of the Sundial), and I bet if we took the time to really dig deep, we could find more songs with this concept more than we think.
What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?
According to many articles, the discovery of the circle goes way back before recorded history. It started with the Egyptians (the inventors of Geometry) who invented the wheel. I find this intriguing that the people following the Egyptians “investigated” a simple man made tool, the wheel, to go about finding the equation of a circle. I want to emphasize this point because there is so much in life relating to math if only we stop to look and/or think about it more in depth! Furthermore, Euclid (naturally), contributed to the finding of the properties of the circle and “problems of inscribing polygons” (“Circle”, n.d.). Around 650 BC, Thales, a mathematical philosopher who contributed to various elementary geometry theorems, contributed to the theorems regarding circles. Nearly 400 years later, Apollonius, “a Greek mathematician known as ‘The Great Geometer’”, also contributed to the finding of the equation for a circle, specifically the equation itself (J J O’Connor and E F Roberts). He founded the bipolar equation “ represent[ing] a circle whose centre divides the line segment between the two fixed points of the system in the ratio n to m” (“Circle”, n.d.). Needless to say, the people who helped create this equation were years apart and it’s pretty cool to see how their work built off of each other over time.
How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?
When it comes to the equation of a circle, using technology would be a great way to visually show students what is happening and understand where the equation comes from. KhanAcademy is a great resource for students to work through problems and furthermore, Desmos could be a resource for students to use at home for homework to check their work and understand how different values for ‘x’ and ‘y’ change the circle. A beneficial video to share/watch with your students would be “Lesson Video: Equation of a Circle”, for it provides a visual representation of how to derive the equation (I think exposing students to how to derive the equation will make the equation easier to understand and how the equation formulated). Giving your students technological resources is beneficial and I bet the students appreciate having multiple resources to help them become more understanding of the subject matter.
http://mathworld.wolfram.com/Circle.html
https://mathshistory.st-andrews.ac.uk/Curves/Circle/
https://mathshistory.st-andrews.ac.uk/Biographies/Apollonius/
In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.
I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).
This student submission comes from my former student Fidel Gonzales. His topic, from Precalculus: vectors in two dimensions.
How can this topic be used in your students’ future courses in mathematics?
When a student learns about vectors in two dimensions, they worry about the magnitude of the vector and the direction that it goes. The direction is kept within its limitations which are up, down, left, and right. A student might be curious as to how this topic can be extended further. The way it extends further is by extending vectors into higher dimensions. It is even possible to extend vectors to the sixth dimension! However, for the sake of showing how vectors in two dimensions extend to future courses in math, we will stick to three-dimensions. Learning about vectors in the second dimension creates groundwork to learn about vectors in the third dimension. With the third dimension, vectors could be seen from our point of view compared to seeing it in the two dimensions on paper. The new perspective of the third dimension in vectors includes up, down, left, right, forward, and backwards. Having the new dimension to account for will give students a bigger tie into how mathematics applies into the real world.
How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?
Vectors in the two dimension is used all around our everyday life and we as people rarely notice it. The most common use of vectors in our culture is a quantity displaying a magnitude and direction. This is normally done on a x and y graph. Now you might be asking yourself, I do not play any types of games that sound like this. I am here to tell you that you do. One game that iPhone users play without noticing this would be a game on gamepigeon called knockout. The game appears to be an innocent game of knocking out your friends’ penguins while keeping yours in the designated box. However, math is involved, and you probably didn’t notice. First you must anticipate where the enemy is going. Then you must decide how strong you want to launch your penguin troopers without making them fall out of the ring. Does that sound familiar? Having to apply a force (magnitude) and direction to a quantity. Congratulations, you have now had fun doing math. Next time you are playing a game, try to see if there is any involvement of vectors in two dimensions involved.![]()
How could you as a teacher create an activity or project that involves your topic?
Vectors in two dimensions has many ways to be incorporated in the classroom. A way to do so while connecting to the real world would be having an activity where the students tell a robot where to go using vectors. The students will have a robot that can walk around and in need of directions. The students will be given maps and asked to create a path for the robot to end up in its destination. Essentially, programming the robot to navigate though a course solely using vectors. If the robot falls or walks too far, then the student will realize that either the magnitude was wrong or the direction. Some students might seem to think this would be impractical to the real world, however, there is always a way to show relevance to students. Towards the end of the activity, the students will be asked to guide me to around the class using vectors. Then to sweeten the deal, they will also be asked to show me on a map being projected to them how to get to McDonald’s. Students will realize that vectors in the second dimension could be used to give directions to somewhere and can be applied to everyday life. They will walk outside of the classroom seeing math in the real world from a different perspective.
References:
In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.
I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).
This student submission comes from my former student Lydia Rios. Her topic, from Precalculus: compound interest.
How did people’s conception of this topic change over time?
While this concept is tied with business which is something that started rapidly changing in the early nineteen hundreds, we have understand that there is an accrued interest on loans long before then. People would loan out seeds or cattle and the interest would be paid after a harvest or with the young of the cattle. Of course now we use this concept mathematically but the concept still holds. We understand that there is a base fee and you must return that fee along with a little more. We then started using this with loose change and then as our currency changed from the gold standard we adapted to a new understanding of compound interest. Today we use the equation , where
is the amount accumulated,
is the principal,
is interest rate,
is the compound period and
is the number of periods.
Compound Interest Is Responsible for Modern Civilization (businessinsider.com)
What are the contributions of various cultures to this topic?
We have all experienced trade over the years. Native Americans would trade corn for other goods and offered payment plus interest with their corn harvest. The Silks Roads was a network of trading routes where China and other countries would trade textiles and other materials. They established the concept of payment and interest for purchases. Banks in America and other countries also have a set principal and a interest, whether this be in reference to your savings account or the billed interest on your credit card purchases. Even the invention of cars played a part on this and how our interest can decrease with the deterioration of the car. Over the years your interest payment can go down as the worth of the car goes down.
How have different cultures throughout time used this topic in their society?
Native Americans used compound interest to create trade deals a maintain some status of peace. China had their silk roads where they turned a profit and tried to maintain a sense of livelihood. For some cultures this was their only source of income, if they didn’t’ make some sort of trade then they had nothing to bring home. For others, such as the Native Americans, the trade itself was to protect their lives and the interest was something they owed. We can even see reference to this with the trade markets in Disney’s Aladdin, Aladdin cannot make a trade as he is a peasant but we see other village people making trades and we grasp the concept of worth from each object.
In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.
I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).
This student submission comes from my former student Chi Lin. Her topic, from Precalculus: computing the cross product of two vectors.
How could you as a teacher create an activity or project that involves your topic?
I found one of the real-life examples of the cross product of two vectors on a website called Quora. One person shares an example that when a door is opened or closed, the angular momentum it has is equal to , where
is the linear momentum of the free end of the door being opened or closed, and
is the perpendicular distance from the hinges on which the door rotates and the free end of the door. This example gives me an idea to create an example about designing a room. I try to find an example that closes to my idea and I do find an example. Here is the project that I will design for my students. “If everyone here is a designer and belongs to the same team. The team has a project which is to design a house for a client. Your manager, Mr. Johnson provides a detail of the master room to you and he wants you to calculate the area of the master room to him by the end of the day. He will provide every detail of the master room in three-dimension design paper and send it to you in your email. In the email, he provides that the room ABCD with
and
. Find the area of the room (I will also draw the room (parallelogram ABCD) in three dimensions and show students).”
Reference:
https://www.quora.com/What-are-some-daily-life-examples-of-dot-and-cross-vector-products
https://www.nagwa.com/en/videos/903162413640/
How does this topic extend what your students should have learned in previous courses?
This topic is talking about computing cross product of two vectors in three dimensions. First, students should have learned what a vector is. Second, students should know how to represent vectors and points in space and how to distinguish vectors and points. Notice that when students try to write the vector in space, they need to use the arrow. Next, since we are talking about how to distinguish the vectors and the points, here students should learn the notations of vectors and what each notation means. For example, . Notice that
represents the vectors in three dimensions. After understanding the definition of the vectors, students are going to learn how to do the operation of vectors. They start with doing the addition and scalar multiplication, and magnitude. One more thing that students should learn before learning the cross product which is the dot product. However, students should understand and master how to do the vector operation before they learn the dot product since the dot product is not easy. Students should have learned these concepts and do practices to make sure they are familiar with the vector before they learn the cross products.
References:
How did people’s conception of this topic change over time?
Most people have the misconception that the cross product of two vectors is another vector. Also, the majority of calculus textbooks have the same misconception that the cross product of two vectors is just simply another vector. However, as time goes on, mathematicians and scientists can explain by starting from the perspective of dyadic instead of the traditional short‐sighted definition. Also, we can represent the multiplication of vectors by showing it in a geometrical picture to prove that encompasses both the dot and cross products in any number of dimensions in terms of orthogonal unit vector components. Also, by using the way that the limitation of such an entity to exactly a three‐dimensional space does not allow for one of the three metric motions (reflection in a mirror). We can understand that the intrinsic difference between true vectors and pseudo‐vectors.
Reference:
https://www.tandfonline.com/doi/abs/10.1080/0020739970280407