A surprising appearance of e

Here’s a simple probability problem that should be accessible to high school students who have learned the Multiplication Rule:

Suppose that you play the lottery every day for about 20 years. Each time you play, the chance that you win is $1$ chance in $1000$ . What is the probability that, after playing $1000$ times, you never win?

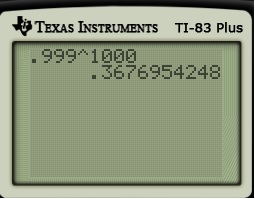
This is a straightforward application of the Multiplication Rule from probability. The chance of not winning on any one play is $0.999$ . Therefore, the chance of not winning $1000$ consecutive times is $(0.999)^{1000}$ , which we can approximate with a calculator.

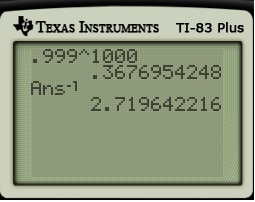
Well, that was easy enough. Now, just for the fun of it, let’s find the reciprocal of this answer.

Hmmm. Two point seven one. Where have I seen that before? Hmmm… Nah, it couldn’t be that.

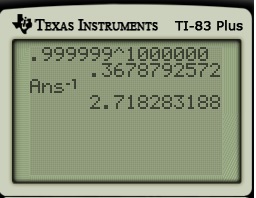
What if we changed the number $1000$ in the above problem to $1,000,000$ ? Then the probability would be $(0.999999)^{1000000}$ .

There’s no denying it now… it looks like the reciprocal is approximately $e$ , so that the probability of never winning for both problems is approximately $1/e$ .

Why is this happening? I offer a thought bubble if you’d like to think about this before proceeding to the answer.

The above calculations are numerical examples that demonstrate the limit

$\displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n = e^x$

In particular, for the special case when $n = -1$ , we find

$\displaystyle \lim_{n \to \infty} \left(1 - \frac{1}{n}\right)^n = e^{-1} = \displaystyle \frac{1}{e}$

The first limit can be proved using L’Hopital’s Rule. By continuity of the function $f(x) = \ln x$ , we have

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \ln \left[ \left(1 + \frac{x}{n}\right)^n \right]$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} n \ln \left(1 + \frac{x}{n}\right)$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \frac{ \displaystyle \ln \left(1 + \frac{x}{n}\right)}{\displaystyle \frac{1}{n}}$

The right-hand side has the form $\infty/\infty$ as $n \to \infty$ , and so we may use L’Hopital’s rule, differentiating both the numerator and the denominator with respect to $n$ .

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \frac{ \displaystyle \frac{1}{1 + \frac{x}{n}} \cdot \frac{-x}{n^2} }{\displaystyle \frac{-1}{n^2}}$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \displaystyle \frac{x}{1 + \frac{x}{n}}$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \frac{x}{1 + 0}$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = x$

Applying the exponential function to both sides, we conclude that

$\displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n= e^x$

In an undergraduate probability class, the problem can be viewed as a special case of a Poisson distribution approximating a binomial distribution if there’s a large number of trials and a small probability of success.

The above calculation also justifies (in Algebra II and Precalculus) how the formula for continuous compound interest $A = Pe^{rt}$ can be derived from the formula for discrete compound interest $A = P \displaystyle \left( 1 + \frac{r}{n} \right)^{nt}$

All this to say, Euler knew what he was doing when he decided that $e$ was so important that it deserved to be named.

A surprising appearance of e

Published by John Quintanilla

Leave a comment Cancel reply

Share this:

Related

Published by John Quintanilla

Leave a comment Cancel reply