continued fractions – Mean Green Math

I suggest the following activity for bright middle-school students who think that they know everything that there is to know about fractions.

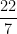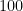The approximation to $\pi$ that is most commonly taught to students is $\displaystyle \frac{22}{7}$ . As I’ll discuss, this is the closest rational number to $\pi$ using a denominator less than $100$ . However, it is possible to obtain closer rational approximations to $\pi$ using larger numbers. Indeed, the ancient Chinese mathematicians were superior to the ancient Greeks in this regard, as they developed the approximation

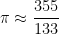
$\pi \approx \displaystyle \frac{355}{133}$

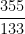It turns out that this is the best rational approximation to $\pi$ using a denominator less than $16,000$ . In other words, $\displaystyle \frac{355}{133}$ is the best approximation to $\pi$ using a reasonably simple rational number.

Step 1. To begin, let’s find $\pi$ with a calculator. Then let’s now subtract $3$ and then find the inverse.

This calculation has shown that

$\pi = \displaystyle 3 + \frac{1}{7.0625133\dots}$

If we ignore the $0.0625133$ , we obtain the usual approximation

$\pi \approx \displaystyle 3 + \frac{1}{7} = \frac{22}{7}$

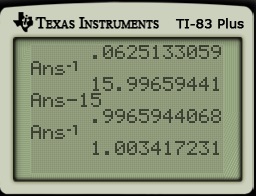
Step 2. However, there’s no reason to stop with one reciprocal, and this might give us some even better approximations. Let’s subtract 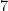$7$ from the current denominator and find the reciprocal of the difference.

At this point, we have shown that

$\pi = \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15.9965944\dots}}$

If we round the final denominator down to $15$ , we obtain the approximation

$\pi \approx \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15}}$

$\pi \approx \displaystyle 3 + \frac{1}{~~~\displaystyle \frac{106}{15}~~~}$

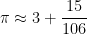
$\pi \approx \displaystyle 3 + \frac{15}{106}$

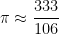
$\pi \approx \displaystyle \frac{333}{106}$

Step 3. Continuing with the next denominator, we subtract $15$ and take the reciprocal again.

At this point, we have shown that

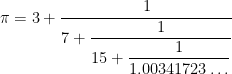
$\pi = \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15 + \displaystyle \frac{1}{1.00341723\dots}}}$

If we round the final denominator down to $1$ , we obtain the approximation

$\pi \approx \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{16}}$

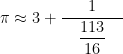
$\pi \approx \displaystyle 3 + \frac{1}{~~~\displaystyle \frac{113}{16}~~~}$

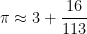
$\pi \approx \displaystyle 3 + \frac{16}{113}$

$\pi \approx \displaystyle \frac{355}{113}$

Step 4. Let me show one more step.

At this point, we have shown that

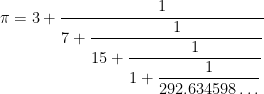
$\pi = \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15 + \displaystyle \frac{1}{1 + \displaystyle \frac{1}{292.634598\dots}}}}$

If we round the final denominator down to 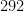$292$ , we (eventually) obtain the approximation

$\pi \approx \displaystyle \frac{52163}{16604}$

The calculations above are the initial steps in finding the continued fraction representation of $\pi$ . A full treatment of continued fractions is well outside the scope of a single blog post. Instead, I’ll refer the interested reader to the good write-ups at MathWorld (http://mathworld.wolfram.com/ContinuedFraction.html) and Wikipedia (http://en.wikipedia.org/wiki/Continued_fraction) as well as the references therein.

But I would like to point out one important property of the convergents that we found above, which were

$\displaystyle \frac{22}{7}, \frac{333}{106}, \frac{355}{113}, ~ \hbox{and} ~ \frac{52163}{16604}$

All of these fractions are pretty close to $\pi$ , as shown below. (The first decimal below is the result for $22/7$ .)

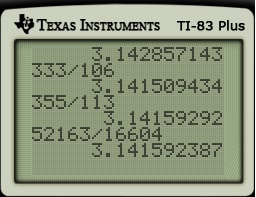
In fact, these are the first terms in a sequence of best possible rational approximations to $\pi$ up to the given denominator. In other words:

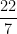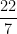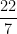$\displaystyle \frac{22}{7}$ is the best rational approximation to $\pi$ using a denominator less than $106$. In other words, no integer over $8$ will be any closer to $\pi$ than $\displaystyle \frac{22}{7}$ . No integer over $9$ will be any closer to $\pi$ than $\displaystyle \frac{22}{7}$ . And so on, all the way up to denominators of $105$ . 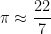Small wonder that we usually teach children the approximation $\pi \approx \displaystyle \frac{22}{7}$ .
Once we reach 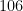$106$ , the fraction $\displaystyle \frac{323}{106}$ is the best rational approximation to $\pi$ using a denominator less than $113$ .
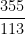Then $\displaystyle \frac{355}{113}$ is the best rational approximation to $\pi$ using a denominator less than $16604$ .

As noted above, the ancient Chinese mathematicians were superior to the ancient Greeks in this regard, as they were able to develop the approximation $\pi \approx \displaystyle \frac{355}{113}$ . For example, Archimedes was able to establish that

$3\frac{10}{71} < \pi < 3\frac{1}{7}$

Tag: continued fractions

Decimal Approximations of Logarithms: Index

Continued fractions and pi