Confirming Einstein’s Theory of General Relativity With Calculus, Part 2a: Graphically Exploring Precession

In this series, I’m discussing how ideas from calculus and precalculus (with a touch of differential equations) can predict the precession in Mercury’s orbit and thus confirm Einstein’s theory of general relativity. The origins of this series came from a class project that I assigned to my Differential Equations students maybe 20 years ago.

But what is precession? To explore this concept, let’s explore the graph of

$r = \displaystyle \frac{a}{1 + e \cos (1-k)\theta}$

for various values of $a$ , $e$ , and $k$ using Desmos. (Note that, in this context, the number $e$ does not mean Euler’s constant $2.718\dots$ . The reason for choosing the letter $e$ for this parameter will become clear shortly.) Naturally, this demonstration could also be done with other tools like a graphing calculator.

I suggest beginning by setting $e=0$ and $k=0$ and altering the value of $a$ . This is the easiest behavior to explain. From the equation, $a$ is directly proportional to the distance from the origin $r$ . So, not surprisingly, increasing $a$ produces a larger graph, and decreasing $a$ produces a smaller graph.

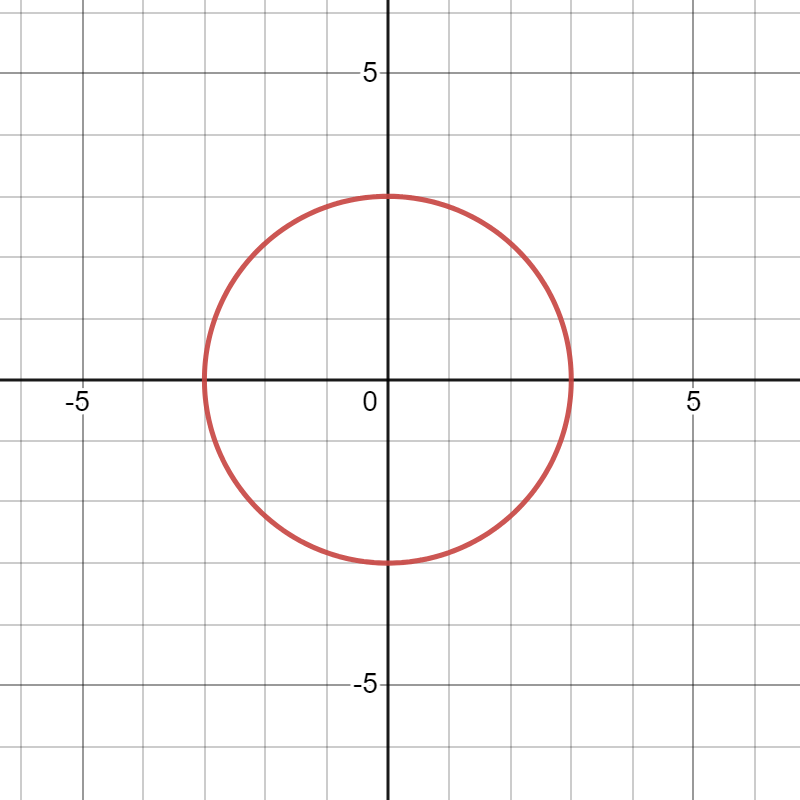
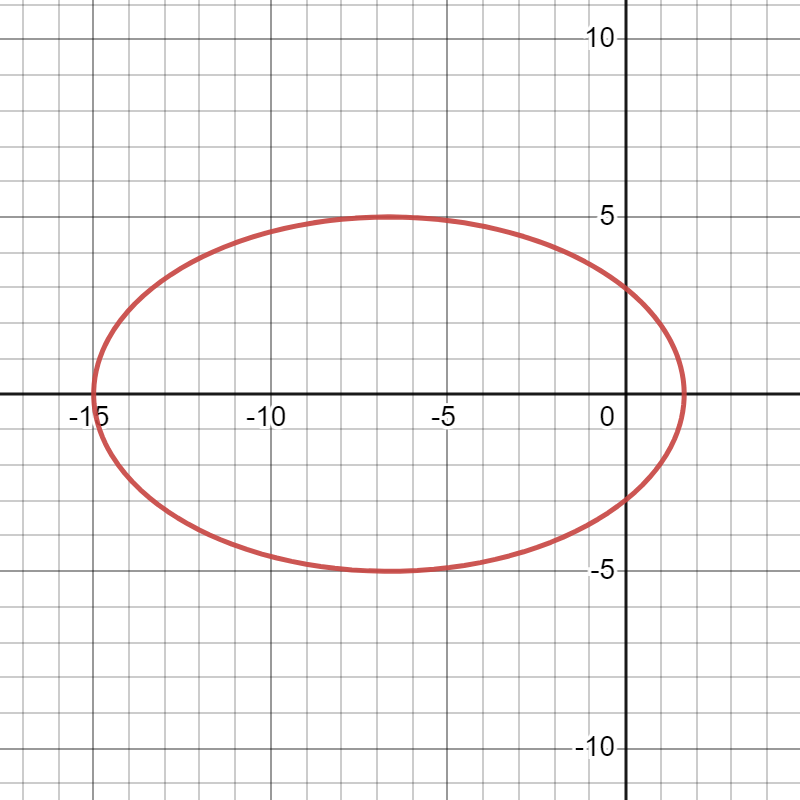
Second, I suggest setting $a=3$ and $k=0$ but altering the value of $e$ . Starting at $e=0$ , the graph is a circle. This makes complete sense: if $e=0$ , then the equation simply becomes $r=a$ , so the distance from the origin is the same for all angles. However, as $e$ increases, the original circle becomes more and more stretched out. We will prove this analytically in a later post, but it turns out that, for $0 < e < 1$ , the graph is an ellipse, and the origin is one of the foci of the ellipse. The number $e$ is called the eccentricity of the ellipse (hence the letter $e$ ).

Again, if the value of $e$ is fixed but $a$ varies, the graph becomes either larger or smaller as $a$ becomes larger or smaller.

We notice that if $0 < e < 1$ and $k=0$ , then the denominator of

$r = \displaystyle \frac{r}{1 + e \cos \theta}$

varies between $1-e$ and $1+e$ . In particular, the denominator is always positive. Therefore, the value of $r$ is least positive — the graph is closest to the origin — when the denominator is greatest. This happens when $\theta$ is a multiple of $2\pi$ . So, for example, when $\theta = 0$ , then $r = a/(1+e)$ is as close as the graph gets to the origin. Let’s call this closest distance $P$ ; in the context of a planet’s orbit around the sun, this represent perihelion. Then we have $P = \displaystyle \frac{a}{1+e}$ .

When $e=1$ , the graph switches from an ellipse to a parabola, where the origin is the focus of the parabola. For $e>1$ , the graph becomes a hyperbola. However, since we’re mostly going to be concerned with stable planetary orbits in this series, we won’t dwell too much on the case $e \ge 1$ .

Third, I suggest setting $a=3$ , $e=0.8$ , and then alter the value of $k$ . For $k=0$ , the graph is simply a single ellipse. However, by changing the value of $k$ , the graph changes into a spiral.

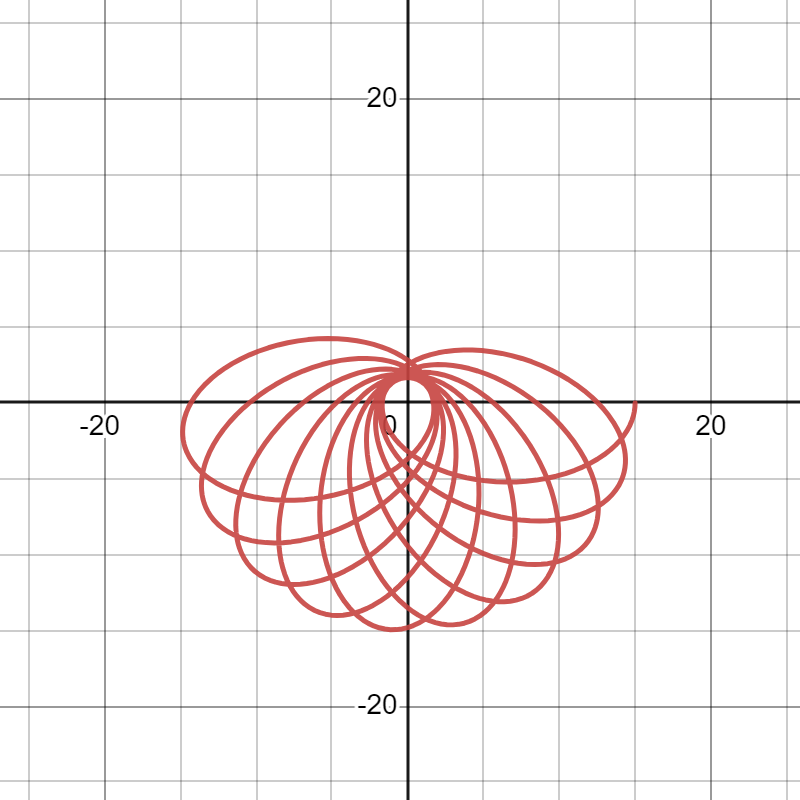
In the above figure, the spiral stopped “spiraling” because I had asked Desmos only to show the graph between $0 \le \theta \le 20 \pi$ . If I had changed the upper bound to something larger than $20\pi$ , the spiral would continue.

The precession in the spiral is defined to be the angular offset between each loop of the spiral. Clearly, this is a function of $k$ . To find this function, we again examine the function

$r = \displaystyle \frac{a}{1 + e \cos (1-k)\theta}$

Once again, if $0 < e < 1$ , then the denominator varies between $1-e$ and $1+e$ . In particular, the denominator is always positive. Therefore, the value of $r$ is least positive when the denominator is greatest, and the denominator is greatest when $(1-k)\theta$ is a multiple of $2\pi$ . So, for example, when $\theta = 0$ , then $r = a/(1+e)$ is as close as the graph gets to the origin.

When does the graph return to its closest point to the origin next? This would occur when $(1-k)\theta = 2\pi$ , or $\theta = \displaystyle \frac{2\pi}{1-k}$ . If $k =0$ , then the angle of closest approach to the origin would $\theta =2\pi$ , and the graph simply cycles over itself. However, if $k > 0$ , then this angle $\theta$ will be larger than $2\pi$ , thus producing a spiral. Indeed, the amount of precession would be equal to

$\displaystyle \frac{2\pi}{1-k} - 2\pi = \frac{2\pi k}{1-k}$ .

In the picture above, $k = 0.05$ . Therefore, the amount of precession would be $\displaystyle \frac{2\pi (0.05)}{1-0.05} = \frac{2\pi}{19}$ radians $\approx 18.95^\circ$ . Therefore, after 19 “leafs” of the spiral, the graph would begin to cycle on top of itself.

Confirming Einstein’s Theory of General Relativity With Calculus, Part 1c: Outline of Argument

This is going to be a very long series, so I’d like to provide a tree-top view of how the argument will unfold.

We begin by using three principles from Newtonian physics — the Law of Conservation of Angular Momentum, Newton’s Second Law, and Newton’s Law of Gravitation — to show that the orbit of a planet, under Newtonian physics, satisfies the initial-value problem

$u''(\theta) + u(\theta) = \displaystyle \frac{GMm^2}{\ell^2}$ ,

$u(0) = \displaystyle \frac{1}{P}$ ,

$u'(0) = 0$ .

In these equations:

The orbit of the planet is in polar coordinates $(r,\theta)$ , where the Sun is placed at the origin.
The planet’s perihelion — closest distance from the Sun — is a distance of $P$ at angle $\theta = 0$ .
The function $u(\theta)$ is equal to $\displaystyle \frac{1}{r(\theta)}$ .
$G$ is the gravitational constant of the universe.
$M$ is the mass of the Sun.
$m$ is the mass of the planet.
$\ell$ is the angular momentum of the planet.

The solution of this differential equation is

$u(\theta) = \displaystyle \frac{1 + \epsilon \cos \theta}{\alpha}$ ,

so that

$r(\theta) = \displaystyle \frac{\alpha}{1 + \epsilon \cos \theta}$ .

In polar coordinates, this is the graph of an ellipse. Substituting $\theta = 0$ , we see that

$P = \displaystyle \frac{1 + \epsilon}{\alpha}$ .

In the solution for $u(\theta)$ , we have $\alpha = \displaystyle \frac{\ell^2}{GMm^2}$ and $\epsilon = \displaystyle \frac{\alpha - P}{P}$ . The number $\epsilon$ is the eccentricity of the ellipse, while $\alpha = \displaystyle \frac{P}{1+\epsilon}$ is proportional to the size of the ellipse.

Under general relativity, the governing initial-value problem changes to

$u''(\theta) + u(\theta) = \displaystyle \frac{GMm^2}{\ell^2} + \frac{3GM}{c^2} [u(\theta)]^2$ ,

$u(0) = \displaystyle \frac{1}{P}$ ,

$u'(0) = 0$ ,

where $c$ is the speed of light. We will see that the solution of this new differential equation can be well approximated by

$u(\theta) = \displaystyle \frac{1 + \epsilon}{\alpha} + \frac{\delta}{\alpha^2} + \frac{\delta \epsilon^2}{2\alpha^2} + \frac{\delta\epsilon}{\alpha^2} \theta \sin \theta - \frac{\delta \epsilon^2}{6\alpha^2} \cos 2\theta - \frac{\delta(3+\epsilon^2)}{3\alpha^2} \cos \theta$

$\approx \displaystyle \frac{1}{\alpha} \left[1 + \epsilon \cos \left(\theta - \frac{\delta \theta}{\alpha} \right) \right]$ .

This last equation describes a spiral that precesses by approximately

$\displaystyle \frac{2\pi \delta}{\alpha} \quad$ radians per orbit

$\displaystyle \frac{6\pi G M}{a c^2 (1-\epsilon^2)} \quad$ radians per orbit,

where $a$ is the length of the semimajor axis of the orbit.

This matches the amount of precession in Mercury’s orbit that is not explained by Newtonian physics, thus confirming Einstein’s theory of general relativity.

To the extent possible, I will take the perspective of a good student who has taken Precalculus and Calculus I. However, I will have to break this perspective a couple of times when I discuss principles from physics and derive the solutions of the above differential equations.

Here we go…

Confirming Einstein’s Theory of General Relativity With Calculus, Part 1b: Precession of Mercury

The figure below shows the (greatly exaggerated) effect of precession on a planet’s otherwise elliptical orbit. In the figure, each perihelion is precessed by an angle of $40^circ$ . After nine orbits, the planet returns to its original position. Suppose, for the sake of argument, that each orbit of the planet depicted in the figure is four months, or one third of Earth’s year. Then the amount of precession would be $40^\circ$ per four months, or $120^\circ$ per year, or $12,000^\circ$ per century.

As I said, the figure above is greatly exaggerated. As we’ll see by the end of this series, Einstein’s general relativity predicts that, on top of the gravitational influences of the other planets, the orbit of Mercury should precess by 43″ of arc per century. That’s a really small angle, since 1 $^\circ$ is equal to 60′ (minutes) of arc and each 1′ is equal to 60″ (seconds) of arc, that means 1″ of arc is the same as $(1/3600)^\circ$ , so that 43″ of arc per century is about $0.012^\circ$ per century. That’s about a million times smaller than the precession of the fictitious planet in the above figure.

How small is $0.012^\circ$ , really?

Courtesy of Wikipedia, the pictures below are the Copernicus crater on the Moon as well as an indicator of its location on the Moon. It is visible with binoculars.

The diameter of the crater is 93 km. Since the Moon is 384,400 km from Earth, that means the angle subtended by the crater, as viewed from the Earth, is about

$\arctan \left( \frac{93}{384,400} \right) \approx 0.014^\circ$ .

So how much is 43″ of arc per century? That’s about the speed as, hypothetically, pointing at the left edge of this lunar crater (which cannot be seen by the naked eye) and then slowly moving your figure so that, about 115 years later, your finger is pointing at the right edge of the crater.

Said another way, the diameter of the Moon is about 3475 km, so that the angle subtended by the Moon, as viewed from the Earth, is about

$\arctan \left( \frac{3745}{384,400} \right) \approx 0.518^\circ$ .

So, at the rate of $0.012^\circ$ per century, it would take $0.518/0.012 \approx 43$ centuries, or about 43,000 years, to trace the angle subtended by the moon.

Needless to say, 43” of arc per century is really, really slow.

Nevertheless, and remarkably, this itty, bitty precession was observable by careful 19th century astronomers with the telescopes that were available then. At the time, this precession was the great unsolved mystery of Newtonian physics that was only answered after two generations later with the discovery of general relativity.

Confirming Einstein’s Theory of General Relativity With Calculus, Part 1a: Introduction

If the universe consisted of only Mercury and the sun, Mercury’s trajectory would trace the same ellipse over and over again. However, there are seven other planets in the solar system (not to mention the dwarf planets), and these planets tug and nudge the orbit of Mercury ever so slightly. (For what it’s worth, similar nudges in the orbit of Uranus led to the discovery of Neptune in 1846.)

The practical effect of these nudges is that the orbit of Mercury precesses, or rotates like a spiral. The figure below shows the (greatly exaggerated) effect of precession on a planet’s otherwise elliptical orbit. In the figure, each perihelion is precessed by an angle of $40^\circ$ . After nine orbits, the planet returns to its original position.

Since the planets are much smaller than the sun and are further away from the Sun than Mercury, this precession is very small. However, this effect can be measured. Every century, the perihelion of Mercury precesses by 574” of arc (roughly a sixth of a degree).

Newton’s Law of Gravitation can be used to calculate the amount of the precession of Mercury; however, they predict a precession of only 531” of arc per century. This discrepancy between observation and prediction was first observed in 1845 and was, for a long time, the outstanding unresolved difficulty in Newtonian physics.

Einstein’s general theory of relativity, which was published seventy years later in 1915, exactly accounts for the missing 43” per century (within the tolerances of observational error). This was the first physical confirmation of general relativity. Furthermore, general relativity predicted that the orbit of Venus also precesses, but by only about 9” of arc per century. This small discrepancy was unobservable in 1915 but was confirmed in 1960. (While not logically necessary, that’s certainly indicative of an accurate scientific theory… not that it merely explains the world but it makes a prediction that is currently unobservable.)

In this series, which might take me a few months to complete, I’m going to explore how to predict the precession in Mercury’s orbit — i.e., confirm Einstein’s theory of general relativity — using tools only from calculus and precalculus. I first introduced these ideas as a class project for my Differential Equations students maybe 20 years ago. As we’ll see, in a couple spots, ideas from first-semester differential equations can make the steps more rigorous. However, pretty much this whole series should be accessible to a good calculus student.

I should say at the outset that none of the mathematics in this series is particularly original with me. I gladly acknowledge that I first learned the ideas in this series as an undergraduate, when I took an upper-level physics course in mechanics. In particular, pretty much all of the ideas in this series can be found in the textbook Classical Dynamics of Particles and Systems, by S. T. Thornton and J. B. Marion (Brooks Cole, New York, 2003). If I’ve made any contribution, it’s the scaffolding of these ideas to make them accessible to students who won’t be taking (or haven’t yet taken) physics courses beyond the traditional first-year sequence.

The Rocket Scientist Quarterbacking an Unlikely NFL Playoff Contender

I greatly enjoyed this Wall Street Journal article about Joshua Dobbs, currently the quarterback of the Minnesota Vikings. The opening paragraphs:

When quarterback Joshua Dobbs subbed in for the Minnesota Vikings last week and led them to a dramatic victory just days after they traded for him, it amazed his teammates whose names he barely knew when he stepped onto the field.

It also left his former colleagues dumbfounded—which isn’t exactly easy to do considering they’re rocket scientists.

“The quickness that he absorbed that playbook is astounding,” says Scott Colloredo, NASA’s Director of Engineering at Florida’s Kennedy Space Center.

Before Dobbs was a journeyman-turned-sensation for the Vikings, he majored in aerospace engineering at the University of Tennessee, where he was the rare SEC football player to take grueling science classes while also preparing to play in the NFL. Even more remarkably, Dobbs has kept up with the science while making millions of dollars in the pros: he has spent two offseasons moonlighting at NASA, where his bosses give him rave reviews and say he was just like any other engineer working on the Artemis program, except for how he made the football fans in the office giddy with excitement.

His co-workers these days are even happier to have him in their orbit.

What is your go-to dance move?

This is frivolous but fun, and it made me smile. Well done.

View this post on Instagram

Snell’s Law and a mystery novel

Lately, for my own leisure reading, I’ve been enjoying the murder-mystery novels of Dorothy Sayers. Her books are an enjoyable trip back in time, as she paints a very vivid portrait of English life of during the interwar years of the 1920s and 1930s. (Of course, at the time she was writing, no one had any idea that the Great War would not actually be the war to end all wars, as was the popular sentiment of the time.) Indeed, her first novel was published literally a century ago in 1923. The lead character, Lord Peter Wimsey (back then, the aristocracy was still part of English culture), has a distinctive way of speaking that makes the novels so delightful. A hallmark of the Sayers novels is that she didn’t merely write whodunit stories; instead, she strove to write novels in which a detective story happens to happen.

As an aside, I learned in her novel Gaudy Night that the adjective Oxonian means “related to Oxford,” which led me to further learn that my hometown of Oxon Hill, Maryland was so named because somebody, centuries ago, thought that the landscape of that part of the state reminded him of Oxford, England. While that comparison might have been reasonable centuries ago, it certainly would raise eyebrows today.

Anyway, with all that as background, in her story Unnatural Death, the following figure depicts an aerial view of a witness’s testimony at a key point in the story. I think I can describe this much of the scene without giving away the plot: the witnesses stood just inside the door of elderly Miss Dawson’s bedroom. A screen blocked direct observation of Miss Dawson as she lay in bed, but the witnesses could see Miss Dawson in the mirror.

As I read the novel, I immediately noticed that the mirror in the figure was not a perfect reflector… at the mirror, the angles of reflection of the dashed path of light are quite different. Indeed, I pulled out my protractor: the angle where the word “Mirror” is located has a measure of about 52 degrees, while the opposite reflected angle has a measure of about 72 degrees.

As this is was part of a murder-mystery novel, I thought: what could be the cause of this disparity? To be a good detective, any explanation, no matter how implausible, must be thought of and reasoned out.

One explanation of the different angles is that, somehow, the speed of light changed in the room. This is the same principle behind Snell’s Law, which explains the refraction of light as it travels between air and water. Since the speed of light in air ( $c_1$ ) is different than the speed of light in water ( $c_2$ ), the angle of incidence ( $\theta_1)$ is different from the angle of refraction ( $\theta_2$ ), but they are related through the formula

$\displaystyle \frac{\sin \theta_1}{c_1} = \frac{\sin \theta_2}{c_2}$ .

This relationship occurs because of Fermat’s principle, which says that light always travels in a path that requires the least amount of time. Ordinarily, this means that light travels in a straight line. However, if the speed of light should change (say, when traveling through both air and water), then the path of the light is refracted.

Fermat’s principle also explains why light reflects at equal angles if the speed of light is constant (as amusingly illustrated in this PBS video by Dianna Cowern, a.k.a. Physics Girl). However, if the speed of light should somehow change in the room at the point where the light reflects, then the light would bounce at a different angle for the same reason that Snell’s Law works.

In this case, the angles $\theta_1$ and $\theta_2$ are complementary to the 52-degree and 72-degree angles, respectively. By the cofunction trigonometric identities, this means that

$\sin \theta_1 = \cos 52^\circ \quad$ and $\quad \sin \theta_2 = \cos 72^\circ$ ,

so that Snell’s Law can be rewritten as

$\displaystyle \frac{c_1}{c_2} = \frac{\cos 52^\circ}{\cos 72^\circ} \approx 1.992$ .

In other words, one explanation for the unusual path of light is that the speed of light was almost exactly twice as fast in one part of room than in the other part… and the exact threshold of this change occurred at the point where the light hit the mirror. Perhaps there was some kind of fog, mist, or other contaminant in the air near poor Miss Dawson that was so thick that light slowed to half its usual speed. So that’s one explanation.

The other explanation, of course, is that the artist who drew the picture just did a lousy job depicting the reflected light.

As this was part of a murder-mystery, both options are still open to investigation. (Yes, that was tongue-in-cheek.)

For what it’s worth, the figure in my book was not exactly the same as Sayers’ original drawing — clearly, modern word processing was used that was unavailable in the 1930s. One of these days, I may visit the Wade Center in Wheaton, Illinois, which has an impressive collection of Sayers’ works, to peruse a first-run printing of Unnatural Death to see if the figure in my book is faithful to the one that appeared when the novel was first published.

Greek letters

Parabolas from String Art: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The links below show my series on numerical integration.

Part 1: Introduction

Part 2: Identifying the highest points of the strings

Part 3: These nine points lie on a parabola: Method #1

Part 4: These nine points lie on a parabola: Method #2

Part 5: These nine points lie on a parabola: Method #3

Part 6: Proof that all of the highest points lie on a parabola without calculus, Part 1

Part 7: Proof that all of the highest points lie on a parabola without calculus, Part 2

Part 8: Proof that all of the highest points lie on a parabola with calculus

Part 9: Proof that the strings are indeed tangent to the parabola, with calculus

Part 10: Conclusion

Geometric Sequence from Rotating an Image

Source: https://xkcd.com/2671/