Trapezoid rule – Mean Green Math

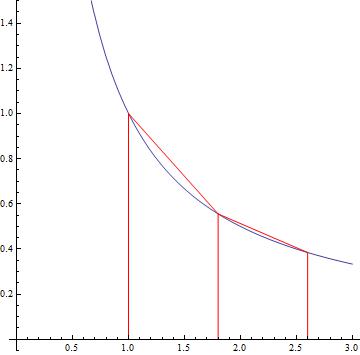
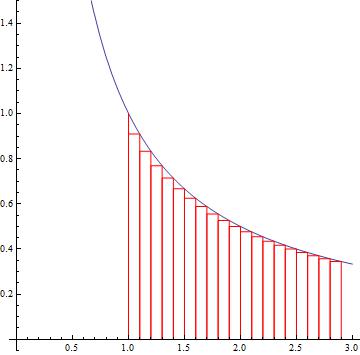
Numerical integration is a standard topic in first-semester calculus. From time to time, I have received questions from students on various aspects of this topic, including:

Why is numerical integration necessary in the first place?
Where do these formulas come from (especially Simpson’s Rule)?
How can I do all of these formulas quickly?
Is there a reason why the Midpoint Rule is better than the Trapezoid Rule?
Is there a reason why both the Midpoint Rule and the Trapezoid Rule converge quadratically?
Is there a reason why Simpson’s Rule converges like the fourth power of the number of subintervals?

In this series, I hope to answer these questions. While these are standard questions in a introductory college course in numerical analysis, and full and rigorous proofs can be found on Wikipedia and Mathworld, I will approach these questions from the point of view of a bright student who is currently enrolled in calculus and hasn’t yet taken real analysis or numerical analysis.

First, let’s talk about why numerical integration is necessary in the first place. Indeed, I can still remember a high school calculus teacher asking me this question nearly 20 years ago, and this question really got me thinking about what we’re collectively teaching in the secondary curriculum. Indeed, in a Calculus I course, it seems like every integral can be computed if only the proper trick is used. We teach students to search for these different tricks:

Let $u = x^2+5$ to find $\displaystyle \int \frac{6x \, dx}{\sqrt{x^2+9}}$ .
Let $x = 3\tan \theta$ to find $\displaystyle \int \frac{6 \, dx}{\sqrt{x^2+9}}$
Use integration by parts to find $\displaystyle \int x^3 e^x \, dx$

In fact, we teach so many tricks that we may give the impression that every integral can be computed if only the proper trick is employed. Indeed, my university hosts an annual “Integration Bee” that challenges students to find the right technique(s) to evaluate some pretty tough integrals.

Unfortunately, not every integral can be solved in terms of a finite number of elementary functions (polynomials, rational functions, exponential functions, logarithms, trigonometric and inverse trigonometric functions). One function that is commonly known to many students which does not have an elementary antiderivative is $\displaystyle \frac{1}{\sqrt{2\pi}} e^{-x^2/2}$ , otherwise known as the bell curve. For most numbers $a$ and $b$ , the area

$\displaystyle \int_a^b \frac{1}{\sqrt{2\pi}} e^{-x^2/2}$

cannot be found exactly, and so we ask students to either use a table in the back of the textbook or else use a function on their scientific calculators to find the answer.

Just for the fun of it, I went through my Ph.D. thesis and wrote down some of the integrals that I had to integrate numerically while in school. As an applied mathematician, I was initially stunned by the teacher’s innocent question because so much of my work would be utterly impossible if it wasn’t for numerical integration. Here are some of the easier ones:

$\displaystyle \int_0^t \frac{1-e^{-x}}{x} dx$
$\displaystyle \int_{2R}^\infty t^2 g(t) \left( \frac{a_1 t^4 + a_2 t^2 + a_3}{(t^2-R^2)^7} +\frac{b_1 t^2 + b_2}{(t^2-R^2)^5} + \frac{c}{(t^2-R^2)^3} \right) dt$
$\displaystyle \int_{d_2}^\infty \int_0^{d_1} \frac{y^2-x^2}{(x^2+y^2)^2} \left(e^{-a(x+d_1)-b d_2} - c\right) dx \, dy$
$\displaystyle \int_{x/2}^\infty \sqrt{r^2 - k^2/4} \phi(r) \, dr$
$\displaystyle \int_{x/2}^\infty \left( \frac{z \sqrt{4r^2-z^2}}{4} + r^2 \arcsin \left( \frac{z}{2r} \right) \right) \phi(r) \, dr$
$\displaystyle \int_0^{2R} e^{-sz} \exp \left[ -c \left( z \sqrt{4R^2-z^2} + 4R^2 \arcsin \frac{z}{2R} \right) \right] dz$
$\displaystyle \int_0^d \exp \left[ -sz - \lambda \left(z - \frac{z^2}{4d} \right) \right] dz$
$\displaystyle \int_d^{d \sqrt{2}} \exp \left[ -sz - \lambda \left( \frac{d (\pi+1)}{2} - d \arcsin \frac{d}{z} + \frac{z^2}{4d} - \sqrt{z^2-d^2} \right) \right] dz$
$\displaystyle \int_0^\infty \exp \left[-sz - \eta \left(1 - e^{-cz/2} - \frac{cz}{4} e^{-cz/2} \right) \right] dz$
$\displaystyle \int_{-\infty}^x \frac{e^t}{t} dt$

All this to say, there are plenty of integrals that arise from a real-world context that have a numerical answer but cannot be computed using the techniques commonly taught in the first-year calculus sequence.

In this series of posts, we have seen that the number $e$ can be thought about in three different ways.

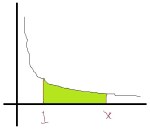1. $e$ defines a region of area 1 under the hyperbola $y = 1/x$ .2. We have the limits

$e = \displaystyle \lim_{h \to 0} (1+h)^{1/h} = \displaystyle \lim_{n \to \infty} \left(1 + \frac{1}{n} \right)^n$ .

These limits form the logical basis for the continuous compound interest formula.

3. We have also shown that $\frac{d}{dx} \left(e^x \right) = e^x$ . From this derivative, the Taylor series expansion for $e^x$ about $x = 0$ can be computed:

$e^x = \displaystyle \sum_{n=0}^\infty \frac{x^n}{n!}$

Therefore, we can let $x = 1$ to find $e$ :

$e = \displaystyle \sum_{n=0}^\infty \frac{1}{n!} = \displaystyle 1 + 1 + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \dots$

Let’s now consider how the decimal expansion of $e$ might be obtained from these three different methods.

1. Finding $e$ using only the original definition is a genuine pain in the neck. The only way to approximate $e$ is by trapping the value of $e$ using various approximation. For example, consider the picture below, showing the curve $y = 1/x$ and trapezoidal approximations on the intervals $[1,1.8]$ and $[1.8,2.6]$ . (Because I need a good picture, I used Mathematica and not Microsoft Paint.)

Each trapezoid has a (horizontal) height of $h = 0.8$ . Furthermore, the bases of the first trapezoids have length $\displaystyle \frac{1}{1} = 1$ and $\displaystyle \frac{1}{1.8}$ , while the bases of the second trapezoid of length $\displaystyle \frac{1}{1.8}$ and $\displaystyle \frac{1}{2.6}$ . Notice that the trapezoids extend above the hyperbola, so that

$\displaystyle \int_1^{2.6} \frac{dx}{x} < \displaystyle \frac{0.8}{2} \left( 1 + \frac{1}{1.8} \right) + \frac{0.8}{2} \left( \frac{1}{1.8} + \frac{1}{2.6} \right)$

$\displaystyle \int_1^{2.6} \frac{dx}{x} < 0.9983 < 1$

However, the number $e$ is defined to be the place where the area under the curve is exactly equal to $1$ , and so

$\displaystyle \int_1^{2.6} \frac{dx}{x} < \displaystyle \int_1^{e} \frac{dx}{x}$

In other words, we know that the area between $1$ and $2.6$ is strictly less than $1$ , and therefore a number larger than $2.6$ must be needed to obtain an area equal to $1$ .

Great, so $e > 2.6$ . Can we do better? Sadly, with two equal-sized trapezoids, we can’t do much better. If the height of the trapezoids was $h$ and not $0.8$ , then the sum of the areas of the two trapezoids would be

$\displaystyle \frac{h}{2} \left( 1 + \frac{2}{1+h} + \frac{1}{1+2h} \right)$

By either guessing and checking — or with the help of Mathematica — it can be determined that this function of $h$ is equal to 1 at approximately $h \approx 0.8019$ , thus establishing that $e > 1 + 2h \approx 2.6039$ .

We can try to better with additional trapezoids. With four trapezoids, we can establish that $e > 2.6845$ .

With 100 trapezoids, we can show that $e > 2.71822$ .

However, trapezoids can only provide a lower bound on $e$ because the original trapezoids all extend over the hyperbola.

To obtain an upper bound on $e$ , we will use a lower Riemann sum to approximate the area under the curve. For example, notice the following picture of 19 rectangles of width $h = 0.1$ ranging from $x =1$ to $x = 2.9$ .

The rectangles all lie below the hyperbola. The width of each one is $h = 0.1$ , and the heights vary from $\frac{1}{1.1}$ to $\frac{1}{2.9}$ . Therefore,

$\displaystyle \int_1^{2.9} \frac{dx}{x} > \displaystyle 0.1 \left( \frac{1}{1.1}+ \frac{1}{1.2} + \dots + \frac{1}{2.9} \right)$

$\displaystyle \int_1^{2.9} \frac{dx}{x} > 1.0326 > 1$

In other words, we know that the area between $1$ and $2.9$ is strictly greater than $1$ , and therefore a number smaller than $2.9$ must be needed to obtain an area equal to $1$ . So, in a nutshell, we’ve shown that $e < 2.9$ .

Once again, additional rectangles can provide better and better upper bounds on $e$ . However, since rectangles do not approximate the hyperbola as well as trapezoids, we expect the convergence to be much slower. For example, with 100 rectangles of width $h$ , the sum of the areas of the rectangles would be

$h \displaystyle \left( \frac{1}{1+h} + \frac{1}{1+2h} + \dots + \frac{1}{1+100h} \right)$

It then becomes necessary to plug in numbers for $h$ until we find something that’s decently close to $1$ yet greater than $1$ . Or we can have Mathematica do the work for us:

So with 100 rectangles, we can establish that $e < 2.7333$ . With 1000 rectangles, we can establish that $e < 2.71977$ .

Clearly, this is a lot of work for approximating $e$ . With all of the work shown in this post, we have shown that $e = 2.71\dots$ , but we’re not yet sure if the next digit is $8$ or $9$ .

In the next post, we’ll explore the other two ways of thinking about the number $e$ as well as their computational tractability.

Tag: Trapezoid rule

Thoughts on Numerical Integration (Part 1): Why numerical integration?

Different definitions of e (Part 11): Numerical computation