Calculators and complex numbers (Part 2)

In yesterday’s post, I showed a movie (also provided at the bottom of this post) that calculators can return surprising answers to exponential and logarithmic problems involving complex numbers. In this series of posts, I hope to explain why the calculator returns these results.

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

where $r = |z| = \sqrt{a^2 + b^2}$ and $\tan \theta = b/a$ , with $\theta$ in the appropriate quadrant.

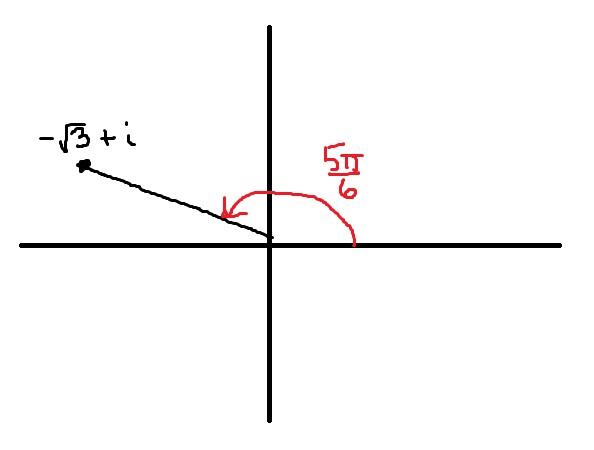
For example, the point $z = -\sqrt{3} + i$ is in the second quadrant of the complex plane. The modulus is

$r = \sqrt{ (-\sqrt{3})^2 + (1)^2 } = \sqrt{4} = 2$ .

(Notice that $1$ , and not $i$ , appears in the above expression.) Also,

$\tan \theta = \displaystyle \frac{1}{-\sqrt{3}}$ , so that $\theta = \displaystyle -\frac{\pi}{6} + n \pi$

Since $-\sqrt{3} + i$ is in the second quadrant, we choose $\theta = \displaystyle -\frac{\pi}{6} + \pi = \displaystyle \frac{5\pi}{6}$ . Therefore,

$-\sqrt{3} + i = \displaystyle 2 \left( \cos \frac{5\pi}{6} + \sin \frac{5\pi}{6} \right)$

This can be checked by simply evaluating the right-hand side and distributing:

$\displaystyle 2 \left( \cos \frac{5\pi}{6} + \sin \frac{5\pi}{6} \right) = \displaystyle 2 \left( -\frac{\sqrt{3}}{2} + i \frac{1}{2} \right) = -\sqrt{3} +i$

When teaching this in class, I’ll run through about 2-4 more examples to make sure that this concept is stuck in my students’ heads.

Notes:

The angle $\theta$ is not uniquely defined… any angle that is coterminal with $\frac{5\pi}{6}$ would also have worked. For example,

$-\sqrt{3} + i = \displaystyle 2 \left( \cos \frac{17\pi}{6} + \sin \frac{17\pi}{6} \right)$

and

$-\sqrt{3} + i = \displaystyle 2 \left( \cos \frac{-7\pi}{6} + \sin \frac{-7\pi}{6} \right)$

It’s really important to remember that $\theta$ need not be equal to $\displaystyle \tan^{-1} \frac{b}{a}$ . After all, the arctangent of an angle must lie between $-\pi/2$ and $\pi/2$ , which won’t work for complex numbers in either the second or third quadrant. That said, it is true that

$-\sqrt{3} + i = \displaystyle -2 \left( \cos \frac{-\pi}{6} + \sin \frac{-\pi}{6} \right)$

The above procedure is also the essence of converting from rectangular coordinates to polar coordinates (or vice versa), which is a function pre-programmed on many scientific calculators.
When teaching this topic, I often use physical humor to get the above points across.

I’ll pick the direction parallel to the chalkboard to be the positive real axis, and the direction perpendicular to the chalkboard (i.e., pointing toward my students) as the positive imaginary axis. I’ll pick some convenient spot in front of the class to be the origin.
Standing at the origin, I’ll face the positive real axis, spin in an angle of $5\pi/6 = 150^\circ$ , and take two steps to arrive at the point $-\sqrt{3} + i$ .
Returning to the origin, I’ll face the positive real axis, spin the other direction in an angle of $-210^\circ$ , and take two steps to arrive at the same point.
Returning to the origin, I’ll face the positive real axis, spin in an angle of $510^\circ$ (getting more than a little dizzy while doing so), and take two steps to arrive at the same point.
Returning to the origin, I’ll face the positive real axis, spin in an angle of only $-30^\circ$ , and take two steps backwards (while doing the moonwalk) to arrive at the same point.

green line

We will need to use this concept of writing a complex number in trigonometric form in order to explain the calculator’s results. For completeness, here’s the movie that I used to begin this series of posts.

Calculators and complex numbers (Part 1)

What is $\ln(-5)$ ? Or $(-8)^{1/3}$ ? Easy, right? Well, let’s plug into a calculator and find out. (Click anywhere in the image below to start the movie. The important stuff is the screen at the top; you can see the keystrokes that I used if you following the mouse arrow toward the bottom.)

In this series of posts, I’ll try to explain why the calculator provides these unexpected answers. This series of posts will have 24 posts (!) and will contain some fairly sophisticated mathematics to explain why the calculator does what it does as well as some pedagogical discussion when I present these topics to my class of future secondary teachers. Each post can be thought of as a 5-10 minute portion of one of my lectures.

Vans

Whenever I see this logo, I feel compelled to find the answer by squaring.

(Shamelessly stolen from a friend.)

Engaging students: Square Roots

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my student Allison Metzler. Her topic, from Pre-Algebra: square roots.

A2. How could you as a teacher create an activity or project that involves your topic?

The following activity, http://ispeakmath.org/2012/05/03/square-roots-with-cheez-its-and-a-graphic-organizer/, effectively engages students because it’s hands-on and allows the students to work together. The students would start with their own cheez-its, creating the smaller squares (1, 4,9). Then, they would work in groups by combining their cheez-its to make bigger squares. Eventually, they would come together as a class to see how big of a square they could create. This involves square roots because each time the student would create a square (assuming they know the properties of a square), they would see that the square root would equal the base of the square. Also, they would see that the base of a square could be any of its four sides because they are all congruent or equal. Thus, the reasoning behind the name, “square root”, would become more apparent. Because they wouldn’t have a calculator as a resource, this visual method of teaching would give the students a more efficient way of calculating square roots. This activity is an effective way to get the students to remember the concept of square roots because it involves food, it’s hands-on, and they’ll learn a visual method of calculating square roots.

D4. What are the contributions of various cultures to this topic?

Many cultures have contributed to the concept of square roots. From 1800 BC to 1600 BC, the Babylonians created a clay tablet proving 2^1/2 and 30*2^1/2 using a square crossed by two diagonals. Within that time (1650 BC), a copy of an earlier work showed how the Egyptians extracted square roots. From 202 BC to 186 BC, the Chinese text Writings on Reckoning described a means to approximate the square roots of two and three. In the 9^th century, the Indian mathematician Mahāvīra stated that square roots of negative numbers do not exist. Then, in 1546, Cantaneo introduced the idea of square roots to Europeans. The last major contribution to the concept of square roots was in 1528 when the German mathematician, Christoph Rudolff, introduced the modern root symbol in print for the first time.

To present this to the students, I would use the following timeline and proceed to briefly mention what each culture contributed to the topic of square roots.

green line

E1. How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

The video, https://www.youtube.com/watch?v=AfBQGLowyKU, uses Elvis’s (You’re So Square) Baby I Don’t Care and recreates it with lyrics relating to square roots. This video not only accurately describes the main components of square roots, but also includes actual examples of perfect squares and square roots. It points out that the square root is the inverse of the square of a number. It also describes the base and the exponent which are directly related to the square root. Because the video is based off an actual song, it should effectively engage students and help them remember it since it’s catchy. Also, it is a great way to introduce the topic to the students where they want to know more, but aren’t overwhelmed with the amount of new information.

References:

Banta, Willy, prod. Think I’m a Square, Baby I Don’t Care. Perf. Elvis Presley. YouTube, 2011. Web. <http://www.youtube.com/watch?v=AfBQGLowyKU>.

Reulbach, Julie. “Square Roots with Cheez-Its and a Graphic Organizer.” I Speak Math., 3 May 2012. Web. <http://ispeakmath.org/2012/05/03/square-roots-with-cheez-its-and-a-graphic-organizer/>.

“Square Root.” Wikipedia. Wikipedia Foundation Inc., 10 Jan. 2014. Web. <http://en.wikipedia.org/wiki/Square_root#History>.

For your enjoyment:

Why do we still require students to rationalize denominators?

Which answer is simplified: $\displaystyle \frac{1}{2 \sqrt{2}}$ or $\displaystyle \frac{ \sqrt{2} }{4}$ ? From example, here’s a simple problem from trigonometry:

Suppose $\theta$ is an acute angle so that $\sin \theta = \displaystyle \frac{1}{3}$ . Find $\tan \theta$ .

To solve, we make a right triangle whose side opposite of $\theta$ has length $1$ and hypotenuse with length $3$ . The adjacent side has length $\sqrt{3^2 - 1^2} = \sqrt{8} = 2\sqrt{2}$ . Therefore,

$\tan \theta = \displaystyle \frac{ \hbox{Opposite} }{ \hbox{Adjacent} } = \displaystyle \frac{1}{2 \sqrt{2}}$

This is the correct answer, and it could be plugged into a calculator to obtain a decimal approximation. However, in my experience, it seems that most students are taught that this answer is not yet simplified, and that they must rationalize the denominator to get the “correct” answer:

$\tan \theta = \displaystyle \frac{1}{2 \sqrt{2}} \cdot \frac{ \sqrt{2} }{ \sqrt{2} } = \displaystyle \frac{ \sqrt{2} }{4}$

Of course, this is equivalent to the first answer. So my question is philosophical: why are students taught that the first answer isn’t simplified but the second is? Stated another way, why is a square root in the numerator so much more preferable than a square root in the denominator?

Feel free to correct me if I’m wrong, but it seems to me that rationalizing denominators is a vestige of an era before cheap pocket calculators. Let’s go back in time to an era before pocket calculators… say, 1927, when The Jazz Singer was just released and stars of silent films, like Don Lockwood, were trying to figure out how to act in a talking movie.

Before cheap pocket calculators, how would someone find $\displaystyle \frac{1}{2 \sqrt{2}} ~~$ or $~~ \displaystyle \frac{ \sqrt{2} }{4}$ to nine decimal places? Clearly, the first step is finding $\sqrt{2}$ by hand, which I discussed in a previous post. So these expressions reduce to

$\displaystyle \frac{1}{2 (1.41421356\dots)}$ or $\displaystyle \frac{1.41421356\dots}{4}$

Next comes the step of dividing. If you don’t have a calculator and had to use long division, which would rather do: divide by $4$ or divide by $2.82842712\dots$ ?

Clearly, long division with $4$ is easier.

It seems to me that ease of computation was the reason that rationalizing denominators was required of students in previous generations. So I’m a little bemused why rationalizing denominators is still required of students now that cheap calculators are so prevalent.

Lest I be misunderstood, I absolutely believe that all students should be able to convert $\displaystyle \frac{1}{2 \sqrt{2}}$ into $\displaystyle \frac{ \sqrt{2} }{4}$ . But I see no compelling reason why the “simplified” answer to the above trigonometry problem should be the second answer and not the first.

A curious square root (Part 2)

There are two natural ways of computing $\sin 15^o$ using trig identities.

Method #1.

$\sin 15^o = \sin(45^o - 30^o)$

$\sin 15^o = \sin 45^o \cos 30^o - \cos 45^o \sin 30^o$

$\sin 15^o = \displaystyle \frac{\sqrt{2}}{2} \cdot \frac{1}{2} - \frac{\sqrt{2}}{2} \cdot \frac{1}{2}$

$\sin 15^o = \displaystyle \frac{\sqrt{6} - \sqrt{2}}{4}$

The same expression would be obtained if we had started with $15^o = 60^o - 45^o$ .

Method #2. Since $15^o$ is in the first quadrant,

$\sin 15^o = \sin \displaystyle \left( \frac{1}{2} \cdot 30^o \right)$

$\sin 15^o = \displaystyle \sqrt{ \frac{1 - \cos 30^o}{2} }$

$\sin 15^o = \displaystyle \sqrt{ \frac{1 - \displaystyle \frac{\sqrt{3}}{2}}{2} }$

$\sin 15^o = \displaystyle \sqrt{ \frac{2 -\sqrt{3}}{4} }$

$\sin 15^o = \displaystyle \frac{ \sqrt{2 -\sqrt{3}}}{2}$

Therefore,

$\displaystyle \frac{\sqrt{6} - \sqrt{2}}{4} = \displaystyle \frac{ \sqrt{2 -\sqrt{3}}}{2}$ ,

which may be verified by squaring both sides.

A curious square root (Part 1)

Here’s a square root that looks like a total mess:

$\sqrt{5 - \sqrt{6} + \sqrt{22+8\sqrt{6}}}$

Just look at this monstrosity, which has a triply-embedded square root! But then look what happens when I plug into a calculator:

Hmmm. How is that possible?!?!

I’ll give the answer after the thought bubble, if you’d like to think about it before seeing the answer.

Let’s start from the premise that $\sqrt{5 - \sqrt{6} + \sqrt{22+8\sqrt{6}}} = 3$ and work backwards. This isn’t the best of logic — since we’re assuming the thing that we’re trying to prove in the first place — but it’s a helpful exercise to see exactly how this happened.

$\sqrt{5 - \sqrt{6} + \sqrt{22+8\sqrt{6}}} = 3$

$5 - \sqrt{6} + \sqrt{22+8\sqrt{6}} = 9$

$\sqrt{22+8\sqrt{6}} = 4 + \sqrt{6}$

$22 + 8 \sqrt{6} = (4 + \sqrt{6})^2$

This last line is correct, using the formula $(a+b)^2 = a^2 + 2ab + b^2$ . So, running the logic from bottom to top (and keeping in mind that all of the terms are positive), we obtain the top equation.

This suggests a general method for constructing such hairy square roots. To begin, start with any similar expression, such as

$(2 - \sqrt{3})^2 = 4 - 4\sqrt{3} + 3$

$(2 - \sqrt{3})^2 = 7 - 4\sqrt{3}$

Then we create a nested square root:

$2 - \sqrt{3} = \sqrt{7 - 4\sqrt{3}}$

Then I get rid of the square root on the left hand side:

$2 = \sqrt{3} + \sqrt{7 - 4\sqrt{3}}$

Then I add or subtract something so that the left-hand side becomes a perfect square.

$25 = 23 + \sqrt{3} + \sqrt{7 - 4 \sqrt{3}}$

Finally, I take the square root of both sides:

$5 = \sqrt{23 + \sqrt{3} + \sqrt{7 - 4 \sqrt{3}}}$

Then I show the right-hand side to my students, ask them to plug into their calculators, and ask them to figure out what happened.

Square roots with a calculator (Part 11)

This is the last in a series of posts about square roots and other roots, hopefully providing a deeper look at an apparently simple concept. However, in this post, we discuss how calculators are programmed to compute square roots quickly.

Today’s movie clip, therefore, is set in modern times:

So how do calculators find square roots anyway? First, we recognize that $\sqrt{a}$ is a root of the polynomial $f(x) = x^2 - a$ . Therefore, Newton’s method (or the Newton-Raphson method) can be used to find the root of this function. Newton’s method dictates that we begin with an initial guess $x_1$ and then iteratively find the next guesses using the recursively defined sequence

$x_{n+1} = x_n - \displaystyle \frac{f(x_n)}{f'(x_n)}$

For the case at hand, since $f'(x) = 2x$ , we may write

$x_{n+1} = x_n - \displaystyle \frac{x_n^2 -a}{2 x_n}$ ,

which reduces to

$x_{n+1} = \displaystyle \frac{2x_n^2 - (x_n^2 -a)}{2 x_n} = \frac{x_n^2 + a}{2x_n} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right)$

This algorithm can be programmed using C++, Python, etc.. For pedagogical purposes, however, I’ve found that a spreadsheet like Microsoft Excel is a good way to sell this to students. In the spreadsheet below, I use Excel to find $\sqrt{2000}$ . In cell A1, I entered $1000$ as a first guess for $\sqrt{2000}$ . Notice that this is a really lousy first guess! Then, in cell A2, I typed the formula

=1/2*(A1+2000/A1)

So Excel computes

$x_2 = \frac{1}{2} \left( x_1 + \displaystyle \frac{2000}{x_1} \right) = \frac{1}{2} \left( 1000 + \displaystyle \frac{2000}{1000} \right) = 501$ .

Then I filled down that formula into cells A3 through A16.

Notice that this algorithm quickly converges to $\sqrt{2000}$ , even though the initial guess was terrible. After 7 steps, the answer is only correct to 2 significant digits ( $45$ ). After 8 steps, the answer is correct to 4 significant digits ( $44.72$ ). On the 9th step, the answer is correct to 9 significant digits ( $44.7213595$ ).

Indeed, there’s a theorem that essentially states that, when this algorithm converges, the number of correct digits basically doubles with each successive step. That’s a lot better than the methods shown at the start of this series of posts which only produced one extra digit with each step.

This algorithm works for finding $k$ th roots as well as square roots. Since $\sqrt[k]{a}$ is a root of $f(x) = x^k - a$ , Newton’s method reduces to

$x_{n+1} = x_n - \displaystyle \frac{x_n^k - a}{k x_n^{k-1}} = \displaystyle \frac{(k-1) x_n^k + a}{k x_n^{k-1}} = \displaystyle \frac{k-1}{k} x_k + \frac{1}{k} \cdot \frac{a}{x_n}$ ,

which reduces to the above sequence if $k =2$ .

See also this Wikipedia page for further historical information as well as discussion about how the above recursive sequence can be obtained without calculus.

Square roots and logarithms without a calculator (Part 8)

I’m in the middle of a series of posts concerning the elementary operation of computing a root. This is such an elementary operation because nearly every calculator has a $\sqrt{~~}$ button, and so students today are accustomed to quickly getting an answer without giving much thought to (1) what the answer means or (2) what magic the calculator uses to find roots. I like to show my future secondary teachers a brief history on this topic… partially to deepen their knowledge about what they likely think is a simple concept, but also to give them a little appreciation for their elders.

To begin, let’s again go back to a time before the advent of pocket calculators… say, 1952.

This story doesn’t go back to 1952 but to Boxing Day 2012 (the day after Christmas). For some reason, my daughter — out of the blue — asked me to compute $\sqrt[19]{25727}$ without a calculator. As my daughter adores the ground I walk on — and I want to maintain this state of mind for as long as humanly possible — I had no choice but to comply. So I might as well have been back in 1952.

In the past few posts, I discussed how log tables and slide rules were used by previous generations to perform this calculation. The problem was that all of these tools were in my office and not at home, and hence were not of immediate use.

The good news is that I had a few logarithms memorized:

$\log_{10} 2 \approx 0.301$ , $\log_{10} 3 \approx 0.477$ , $\log_{10} 7 = 0.845$ ,

and $\ln 10 = 2.3$ .

I had the first two logs memorized when I was a child; the third I memorized later. As I’ll describe, the first three logarithms can be used with the laws of logarithms to closely approximate the base-10 logarithm of nearly any number. The last logarithm was important in previous generations for using the change-of-base formula from $\log_{10}$ to $\ln$ . It was also prominently mentioned in the chapter “Lucky Numbers” from a favorite book of my childhood, Surely You’re Joking Mr. Feynman, so I had that memorized as well.

I also knew that $\ln(1+x) \approx x$ for $x = 0$ from the Taylor expansion of $\ln(1+x)$ .

To begin, I first noticed that $25727 \approx 25600$ , and I knew I could get $\log_{10} 25600$ since $25600 = 2^8 \times 100$ . So I started with

$\log_{10} 25727 = \log_{10} \left(100 \times 256 \times \displaystyle \frac{257.27}{256} \right)$

$\log_{10} 25727 \approx \log_{10} 100 + 8 \log_{10} 2 + \log_{10} 1.005$

$\log_{10} 25727 \approx 2 + 8(0.301) + \displaystyle \frac{\ln 1.005}{\ln 10}$

$\log_{10} 25727 \approx 4.408 + \displaystyle \frac{0.005}{2.3}$

$\log_{10} 25727 \approx 4.408 + 0.002$

$\log_{10} 25727 \approx 4.410$

I did all of the above calculations by hand, cutting off after three decimal places (since I had those base-10 logarithms memorized to only three decimal places). Therefore,

$\log_{10} 25727^(1/19) = \displaystyle \frac{1}{19} \log_{10} 25727 \approx \displaystyle \frac{4.410}{19} \approx 0.232$

So, to complete the calculation, I had to find the value of $x$ so that $\log_{10} x = 0.232$ . This was by far the hardest step, since it could only be done by trial and error. I forget exactly what steps I tried, but here’s a sample:

$\log_{10} 2 \approx 0.301$ . Too big.

$\log_{10} 1.5 = \log_{10} \displaystyle \frac{3}{2} = \log_{10} 3 - \log_{10} 2 \approx 0.477 - 0.301 = 0.176$ . Too small.

$\log_{10} 1.6 = \log_{10} \displaystyle \frac{2^4}{10} = 4\log_{10} 2 - \log_{10} 10 \approx 4(0.301) - 1 = 0.203$ . Too small.

$\log_{10} 1.8 = \log_{10} \displaystyle \frac{2 \cdot 3^2}{10} \approx 0.301 + 2(0.477) - 1 = 0.255$ . Too big.

Eventually, I got to

$\log_{10} 1.71 = \log_{10} \displaystyle \frac{3^2 \cdot 19}{100}$

$\log_{10} 1.71 = 2\log_{10} 3 + \log_{10} 19 - \log_{10} 100$

$\log_{10} 1.71 \approx 2(0.477) + \displaystyle \frac{\log_{10} 18 + \log_{10} 20}{2} - 2$

$\log_{10} 1.71 \approx -1.046 + \frac{1}{2} (\log_{10} 2 + 2 \log_{10} 3 + \log_{10} 2 + \log_{10} 10)$

$\log_{10} 1.71 \approx -1.046 + \frac{1}{2}(2.556)$

$\log_{10} 1.71 \approx 0.232$

So, after a hour or two of arithmetic, I told her my answer: $\sqrt[19]{25727} \approx 1.71$ . You can imagine my sheer delight when we checked my answer with a calculator:

In Part 9, I’ll discuss my opinion about whether or not these kinds of calculations have any pedagogical value for students learning logarithms.

Square roots and logarithms without a calculator (Part 7)

I’m in the middle of a series of posts concerning the elementary operation of computing a square root. This is such an elementary operation because nearly every calculator has a $\sqrt{~~}$ button, and so students today are accustomed to quickly getting an answer without giving much thought to (1) what the answer means or (2) what magic the calculator uses to find square roots. I like to show my future secondary teachers a brief history on this topic… partially to deepen their knowledge about what they likely think is a simple concept, but also to give them a little appreciation for their elders.

Today’s topic — slide rules — not only applies to square roots but also multiplication, division, and raising numbers to any exponent (not just to the $1/2$ power). To begin, let’s again go back to a time before the advent of pocket calculators… say, the 1950s.

Nearly all STEM professionals were once proficient in the use of slide rules. I never learned how to use one as a student. As a college professor, I bought a fairly inexpensive one from Slide Rule Universe. If you’ve never seen a slide rule, here’s a picture of a fairly advanced one. There are multiple rows of numbers and a sliding plastic piece that has a thin vertical line, allowing direct correspondence from one row of numbers to another. (The middle rows are on a piece that slides back and forth; this is necessary for doing multiplication and division with a slide rule.)

Let’s repeat the problem from Part 6 and try to find

$\log_{10} x = \log_{10} \sqrt{4213} = \log_{10} (4213)^{1/2} = \displaystyle \frac{1}{2} \log_{10} 4213$ .

We recall that $\log_{10} 4213 = 3 + \log_{10} 4.213$ . The logarithm on the right-hand side can be estimated by looking at a slide rule. Here’s a picture from my slide rule:

The important parts of this picture are the bottom two rows. Note that the thin red line is lined up between $4.2$ and $4.25$ ; indeed, the red line is about one-third of way from $4.2$ to $4.25$ . On the bottom row, the thin red line is lined up with $0.626$ . So we estimate that $\log_{10} 4213 \approx 3.626$ , so that $\log_{10} \sqrt{4213} \approx \frac{1}{2} (3.626) = 1.813$ .

Working the other direction, we must find $10^{1.813} = 10 \times 10^{0.813}$ . We move the thin red line to a different part of the slide rule:

This time, the thin red line is lined up with $0.813$ on the bottom row. On the row above, the red line is lined up almost exactly on $6.5$ , but perhaps a little to the left of $6.5$ . So we estimate that $10^{1.813} \approx 64.9$ or $64.95$ .

The correct answer is $64.907\dots$ .

Not bad for a piece of plastic.

Because taking square roots is so important, many slide rules have lines that simulate a square-root function… without the intermediate step of taking logarithms. Let’s consider again at the above picture, but this time let’s look at the second row from the top. Notice that the thin red line goes between $42$ and $42.5$ on the second line. (FYI, the line repeats itself to the left, so that the user can tell the difference between $42$ and $4.2$ .) Then looking down to the second line from the bottom, we see that the square root is a little less than $65$ , as before.

In addition to square roots, my personal slide rule has lines for cube roots, sines, cosines, and tangents. In the past, more expensive slide rules had additional lines for the values of other mathematical functions.