What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 2

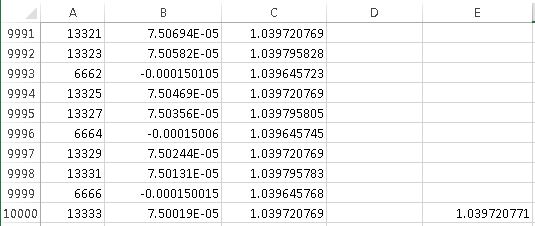
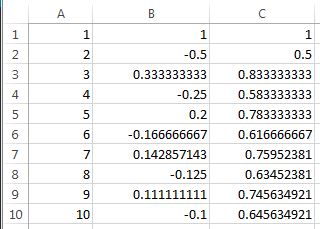
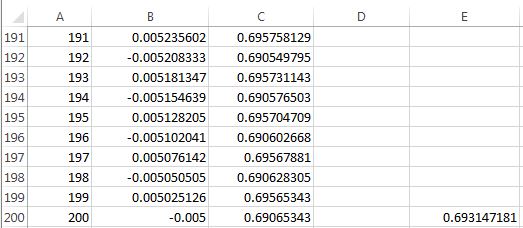
Let’s define partial sums of the harmonic series as follows:

$H(m,n) = \displaystyle \frac{1}{m} + \frac{1}{m+1} + \frac{1}{m+2} + \dots + \frac{1}{n-1} + \frac{1}{n}$ ,

where $m < n$ are positive integers. Here are a couple of facts that I didn’t know before reading Gamma (pages 24-25):

$H(m,n)$ is never equal to an integer.
The only values of $n$ for which $H(1,n)$ is an integer are $n = 2$ and $n=6$ .

When I researching for my series of posts on conditional convergence, especially examples related to the constant $\gamma$ , the reference Gamma: Exploring Euler’s Constant by Julian Havil kept popping up. Finally, I decided to splurge for the book, expecting a decent popular account of this number. After all, I’m a professional mathematician, and I took a graduate level class in analytic number theory. In short, I don’t expect to learn a whole lot when reading a popular science book other than perhaps some new pedagogical insights.

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.

What I Learned from Reading “Gamma: Exploring Euler’s Constant” by Julian Havil: Part 1

Boy, was I wrong. As I turned every page, it seemed I hit a new factoid that I had not known before.

In this series, I’d like to compile some of my favorites — while giving the book a very high recommendation.

It is well known the harmonic series diverges:

$\displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots = \infty$ .

This means that, no matter what number $N$ you choose, I can find a number $n$ so that

$\displaystyle 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots + \frac{1}{n} > N$ .

What I didn’t know (p. 23 of Gamma) is that, in 1968, somebody actually figured out the precise number of terms that are needed for the sum on the left hand side to exceed 100. Here’s the answer:

15,092,688,622,113,788,323,693,563,264,538,101,449,859,497.

With one fewer term, the sum is a little less than 100.

Thoughts on Infinity: Index

I’m doing something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on various lessons I’ve learned while trying to answer the questions posed by gifted elementary school students.

Part 1: Different types of countable sets

Part 2a: Divergence of the harmonic series.

Part 2b: Convergence of the Kempner series.

Part 3a: Conditional convergent series or products shouldn’t be rearranged.

Part 3b: Definition of the Euler-Mascheroni constant $\gamma$ .

Part 3c: Evaluation of the conditionally convergent series $\displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} \dots$

Part 3d: Confirmation of this evaluation using technology.

Part 3e: Evaluation of a rearrangement of this conditionally convergent series.

Part 3f: Confirmation of this different evaluation using technology.

Part 3g: Closing thoughts.

Useless Numerology for 2016: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post.

Part 1: Introduction.

Part 2: $2016 = 2^{10}+2^9+2^8+2^7+2^6+2^5 = 2^{11} - 2^5$ .

Part 3: $2016 = 1 + 2 + \dots + 63$ .

Part 4: $2016 = (1 + 2 + \dots + 9)^2 - (1+2)^2 = 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3$

Part 5: $2016 = \displaystyle \sum_{n=0}^{63} (-1)^{n+1} n^2$

Useless Numerology for 2016: Part 1

The following entertaining (but useless) facts about the number 2,016 appeared in a recent Facebook post (and subsequent comments) by the American Mathematical Monthly.

$2016 = 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3$

$2016 = 2^{10} + 2^9 + 2^8 + 2^7 + 2^6 + 2^5$

$2016 = 1+2+3 + \dots + 62 + 63$

$2016 = \displaystyle \sum_{n=0}^{63} (-1)^{n+1} n^2$

$2016 = (1+2+...+8+9)^2 - (1+2)^2$

$(2 + 0 + 1)! = 6$

$2016 = 2^{11} - 2^5$

$2016 = 2016 \times 1$

The last tongue-in-check equation is my favorite.

In this series, I’ll explain why these different expressions for $2016$ have to be equal to each other. I’ll begin with tomorrow’s post.

Thoughts on Infinity (Part 3g)

We have seen in recent posts that

$latex \displaystyle 1 – \frac{1}{2} + \frac{1}{3} – \frac{1}{4} + \frac{1}{5} – … = \ln 2$

One way of remembering this fact is by using the Taylor series expansion for $\ln(1+x)$ :

$\ln(1+x) = x - \displaystyle \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} \dots$

“Therefore,” the first series can be obtained from the second series by substituting $x=1$ .

I placed “therefore” in quotation marks because this reasoning is completely invalid, even though it happens to stumble across the correct answer in this instance. The radius of convergence for the above Taylor series is 1, which can be verified by using the Ratio Test. So the series converges absolutely for $|x| < 1$ and diverges for $|x| > 1$ . The boundary of $|x| = 1$ , on the other hand, has to be checked separately for convergence.

In other words, plugging in $x=1$ might be a useful way to remember the formula, but it’s not a proof of the formula and certainly not a technique that I want to encourage students to use!

It’s easy to find examples where just plugging in the boundary point happens to give the correct answer (see above). It’s also easy to find examples where plugging in the boundary point gives an incorrect answer because the series actually diverges: for example, substituting $x = -1$ into the geometric series

$\displaystyle \frac{1}{1-x} = 1 + x + x^2 + x^3 + x^4 + \dots$

However, I’ve been scratching my head to think of an example where plugging in the boundary point gives an incorrect answer because the series converges but converges to a different number. I could’ve sworn that I saw an example like this when I was a calculus student, but I can’t see to find an example in reading Apostol’s calculus text.

Thoughts on Infinity (Part 3f)

In recent posts, we’ve seen the curious phenomenon that the commutative and associative laws do not apply to a conditionally convergent series or infinite product: while

$\displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... = \ln 2$ ,

a rearranged series can be something completely different:

$\displaystyle 1 + \frac{1}{3} - \frac{1}{2} + \frac{1}{5} + \frac{1}{7} - \frac{1}{4} + \frac{1}{9} + \frac{1}{11} - \frac{1}{6} ... = \displaystyle \frac{3}{2} \ln 2$ .

This very counterintuitive result can be confirmed using commonly used technology — in particular, Microsoft Excel. In the spreadsheet below, I typed:

=IF(MOD(ROW(A1),3)=0,ROW(A1)*2/3,IF(MOD(ROW(A1),3)=1,4*(ROW(A1)-1)/3+1,4*(ROW(A1)-2)/3+3)) in cell A1
=POWER(-1,A1-1)/A1 in cell B1
=B1 in cell C1
I copied cell A1 into cell A2
=POWER(-1,A2-1)/A2 in cell B2
=C1+B2 in cell C2

The unusual command for cell A1 was necessary to get the correct rearrangement of the series.

Then I used the FILL DOWN command to fill in the remaining rows. Using these commands cell C9 shows the sum of all the entries in cells B1 through B9, so that

$\displaystyle 1 + \frac{1}{3} - \frac{1}{2} + \frac{1}{5} + \frac{1}{7} - \frac{1}{4} + \frac{1}{9} + \frac{1}{11} - \frac{1}{6} \approx 0.961544012$

Filling down to additional rows demonstrates that the sum converges to $\displaystyle \frac{3}{2}\ln 2$ and not to $\ln 2$ . Here’s the sum up to 10,000 terms… the entry in column E is the first few digits in the decimal expansion of $\displaystyle \frac{3}{2} \ln 2$ .

Clearly the partial sums are not approaching $\ln 2 \approx 0.693$ , and there’s good visual evidence to think that the answer is $\displaystyle \frac{3}{2} \ln 2$ instead. (Incidentally, the 10,000th partial sum is very close to the limiting value because $10,000$ is one more than a multiple of 3.)

Thoughts on Infinity (Part 3e)

In recent posts, we’ve seen the curious phenomenon that the commutative and associative laws do not apply to a conditionally convergent series or infinite product. Here’s another classic example of this fact that’s attributed to Cauchy.

We’ve already seen in this series (pardon the pun) that

$\displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... = \ln 2$ .

Let’s now see what happens if I rearrange the terms of this conditionally convergent series. Let

$T = \displaystyle 1 + \frac{1}{3} - \frac{1}{2} + \frac{1}{5} + \frac{1}{7} - \frac{1}{4} + \frac{1}{9} + \frac{11} - \frac{1}{6} \dots$ ,

where two positive numbers alternate with a single negative term. By all rights, this shouldn’t affect anything… right?

Let $s_n$ be the $n$ th partial sum of this series, so that $s_{3n}$ contains $2n$ positive terms with odd denominators and $n$ negative terms with even denominators:

$s_{3n} = \displaystyle \sum_{k=1}^{2n} \frac{1}{2n-1} - \sum_{k=1}^n \frac{1}{2n}$ .

Let me now add and subtract the “missing” even terms in the first sum:

$s_{3n} = \displaystyle \sum_{k=1}^{2n} \frac{1}{2n-1} + \sum_{k=1}^{2n} \frac{1}{2n} - \sum_{k=1}^{2n} \frac{1}{2n} - \sum_{k=1}^n \frac{1}{2n}$

$s_{3n} = \displaystyle \sum_{k=1}^{4n} \frac{1}{n} - \sum_{k=1}^{2n} \frac{1}{2n} - \sum_{k=1}^n \frac{1}{2n}$

$s_{3n} = \displaystyle \sum_{k=1}^{4n} \frac{1}{n} - \frac{1}{2} \sum_{k=1}^{2n} \frac{1}{n} - \frac{1}{2} \sum_{k=1}^n \frac{1}{n}$ .

For reasons that will become apparent, I’ll now rewrite this as

$s_{3n} = \displaystyle \int_1^{4n} \frac{dx}{x} + \left( \sum_{k=1}^{4n} \frac{1}{k} - \displaystyle \int_1^{4n} \frac{dx}{x} \right)$

$- \displaystyle \frac{1}{2} \int_1^{2n} \frac{dx}{x} - \frac{1}{2} \left( \sum_{k=1}^{2n} \frac{1}{k} - \int_1^{2n} \frac{dx}{x} \right)$

$- \displaystyle \frac{1}{2} \int_1^{n} \frac{dx}{x} - \frac{1}{2} \left( \sum_{k=1}^{n} \frac{1}{k} - \int_1^{n} \frac{dx}{x} \right)$ ,

$s_{3n} = \ln(4n) - \ln 1 + \displaystyle \left( \sum_{k=1}^{4n} \frac{1}{k} - [\ln(4n) - \ln 1]\right)$

$- \displaystyle \frac{1}{2}[\ln (2n) - \ln 1] - \displaystyle \frac{1}{2} \left( \sum_{k=1}^{2n} \frac{1}{k} - [\ln (2n) - \ln 1]\right)$

$- \displaystyle \frac{1}{2}[\ln n - \ln 1] - \displaystyle \frac{1}{2} \left( \sum_{k=1}^{n} \frac{1}{k} - [\ln n - \ln 1]\right)$

Since $\ln 1 = 0$ , $\ln(2n) = \ln 2 + \ln n$ , and $\ln(4n) = \ln 4 + \ln n = 2\ln 2 + \ln n$ , we have

$s_{3n} = 2\ln 2 + \ln n + \displaystyle \left( \sum_{k=1}^{4n} \frac{1}{k} - \ln 4n \right)$

$\displaystyle - \frac{\ln 2 + \ln n}{2} - \displaystyle \frac{1}{2} \left( \sum_{k=1}^{2n} \frac{1}{k} - \ln 2n \right)$

$\displaystyle - \frac{\ln n}{2} - \frac{1}{2} \displaystyle \left( \sum_{k=1}^{n} \frac{1}{k} - \ln n \right)$ ,

$s_{3n}= \displaystyle \frac{3}{2}\ln 2 + \displaystyle \left( \sum_{k=1}^{4n} \frac{1}{k} - \ln 4n \right) - \frac{1}{2}\left( \sum_{k=1}^{2n} \frac{1}{k} - \ln 2n\right) - \frac{1}{2}\left( \sum_{k=1}^{n} \frac{1}{k} - \ln n\right)$ .

I now take the limit as $m \to \infty$ :

$\displaystyle \lim_{n \to \infty} s_{3n} = \displaystyle \frac{3}{2}\ln 2 + \lim_{n \to \infty} \left( \sum_{k=1}^{4n} \frac{1}{k} - \ln 4n \right) - \frac{1}{2} \lim_{n \to \infty} \left( \sum_{k=1}^{2n} \frac{1}{k} - \ln 2n\right) - \frac{1}{2} \lim_{n \to \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln n\right)$ .

This step reveals why I added and subtracted the integrals above: those gymnastics were necessary in order to reach a limit that converges.

As shown earlier in this series, if

$\displaystyle \lim_{m \to \infty} \left( \sum_{k=1}^m \frac{1}{k} - \ln m \right) = \gamma$ ,

the Euler-Mascheroni constant. Therefore, since the limit of any subsequence must converge to the same limit, we have

Applying these above, we conclude

$\displaystyle \lim_{m \to \infty} s_{3n} = \displaystyle \frac{3}{2}\ln 2 + \gamma - \frac{1}{2}\gamma - \frac{1}{2} \gamma = \displaystyle \frac{3}{2} \ln 2$ ,

which is different than $\ln 2$ .

Technically, I’ve only shown so far that the limit of partial sums 3, 6, 9, … is $\displaystyle\frac{3}{2} \ln 2$ . For the other partial sums, I note that

$\displaystyle \lim_{n \to \infty} t_{3n+1} = \displaystyle \lim_{n \to \infty} \left(s_{3n} + \displaystyle \frac{1}{4n+1} \right) = \displaystyle \frac{3}{2} \ln 2 + 0 = \displaystyle \frac{3}{2} \ln 2$

and

$\displaystyle \lim_{n \to \infty} t_{3n-1} = \displaystyle \lim_{n \to \infty} \left(s_{3n} - \displaystyle \frac{1}{2n} \right) = \displaystyle \frac{3}{2} \ln 2 - 0 = \displaystyle \frac{3}{2} \ln 2$ .

Therefore, I can safely conclude that

$T = \displaystyle \lim_{n \to \infty} t_n = \displaystyle \frac{3}{2} \ln 2$ ,

which is different than the original sum $S$ .

Thoughts on Infinity (Part 3d)

In yesterday’s post, I showed that

$\displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... = \ln 2$ .

This can be (sort of) confirmed using commonly used technology — in particular, Microsoft Excel. In the spreadsheet below, I typed:

1 in cell A1
=POWER(-1,A1-1)/A1 in cell B1
=B1 in cell C1
=A1+1 in cell A2
=POWER(-1,A2-1)/A2 in cell B2
=C1+B2 in cell C2
Then I used the FILL DOWN command to fill in the remaining rows. Using these commands cell C10 shows the sum of all the entries in cells B1 through B10, so that

$1 - \displaystyle \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} - \frac{1}{8} + \frac{1}{9} - \frac{1}{10} \approx 0.645634921$

Filling down to additional rows demonstrates that the sum converges to $\ln 2$ , albeit very slowly (as is typical for conditionally convergent series). Here’s the sum up to 200 terms… the entry in column E is the first few digits in the decimal expansion of $\ln 2$ .

Here’s the result after 2000 terms:

20,000 terms:

And finally, 200,000 terms. (It takes a few minutes for Microsoft Excel to scroll this far.)

We see that, as expected, the partial sums are converging to $\ln 2$ , as expected. Unfortunately, the convergence is extremely slow — we have to compute 10 times as many terms in order to get one extra digit in the final answer.

Thoughts on Infinity (Part 3c)

Define

$S = \displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ...$

By the alternating series test, this series converges. However,

$\displaystyle \sum_{n=1}^\infty |a_n| = \displaystyle \sum_{n=1} \frac{1}{n}$ ,

which is the divergent harmonic series which was discussed earlier in this series. Therefore, the series $S$ converges conditionally and not absolutely.

To calculate the value of $S$ , let $s_n = \displaystyle \sum_{k=1}^n \frac{(-1)^{k-1}}{k}$ , the $n$ th partial sum of $S$ . Since the series converges, we know that $\displaystyle \lim_{n \to \infty} s_n$ converges. Furthermore, the limit of any subsequence, like $\displaystyle \lim_{n \to \infty} s_{2n}$ , must also converge to $S$ .

If $n$ is even, so that $n = 2m$ and $m$ is an integer, then

$s_{2m} = \displaystyle \sum_{k=1}^n \frac{(-1)^{k-1}}{k}$

$= \displaystyle \sum_{k=1}^{m} \frac{1}{2k-1} - \sum_{k=1}^m \frac{1}{2k}$

$= \displaystyle \left( \sum_{k=1}^{2m} \frac{1}{k} - \sum_{k=1}^m \frac{1}{2k} \right) - \sum_{k=1}^m \frac{1}{2k}$

$= \displaystyle \sum_{k=1}^{2m} \frac{1}{k} - 2 \sum_{k=1}^m \frac{1}{2k}$

$= \displaystyle \sum_{k=1}^{2m} \frac{1}{k} - \sum_{k=1}^m \frac{1}{k}$ .

For reasons that will become apparent, I’ll now rewrite this as

$s_{2m} = \displaystyle \int_1^{2m} \frac{dx}{x} + \left( \sum_{k=1}^{2m} \frac{1}{k} - \displaystyle \int_1^{2m} \frac{dx}{x} \right) - \displaystyle \int_1^m \frac{dx}{x} - \left( \sum_{k=1}^m \frac{1}{k} - \int_1^m \frac{dx}{x} \right)$ ,

$s_{2m} = \ln(2m) - \ln 1 + \displaystyle \left( \sum_{k=1}^{2m} \frac{1}{k} - [\ln(2m) - \ln 1]\right)$

$- [\ln m - \ln 1] - \displaystyle \left( \sum_{k=1}^m \frac{1}{k} - [\ln m - \ln 1]\right)$ .

Since $ln 1 = 0$ and $\ln(2m) = \ln 2 + \ln m$ , we have

$s_{2m} = \ln 2 + \ln m + \displaystyle \left( \sum_{k=1}^{2m} \frac{1}{k} - \ln 2m \right) - \ln m - \displaystyle \left( \sum_{k=1}^m \frac{1}{k} - \ln m \right)$

$= \ln 2 + \displaystyle \left( \sum_{k=1}^{2m} \frac{1}{k} - \ln 2m \right) - \left( \sum_{k=1}^m \frac{1}{k} - \ln m\right)$ .

I now take the limit as $m \to \infty$ :

$\displaystyle \lim_{m \to \infty} s_{2m} = \ln 2 + \displaystyle \lim_{m \to \infty} \left( \sum_{k=1}^{2m} \frac{1}{k} - \ln 2m\right) - \lim_{m \to \infty} \left( \sum_{k=1}^m \frac{1}{k} - \ln m \right)$ .