Lessons from teaching gifted elementary school students (Part 4a)

Every so often, I’ll informally teach a class of gifted elementary-school students. I greatly enjoy interacting with them, and I especially enjoy the questions they pose. Often these children pose questions that no one else will think about, and answering these questions requires a surprisingly depth of mathematical knowledge.

Here’s a question I once received:

What is the chance of winning a game of BINGO after only four turns?

I leave a thought bubble in case you’d like to think this. One way of answering this question appears after the bubble.

green_speech_bubble

When my class posed this question, I was a little concerned that my class was simply not ready to understand the solution (described below), as it takes more than a little work to get at the answer. Still, what I love about this question is that it gave me a way to teach my class some techniques of probabilistic reasoning that probably would not occur in a traditional elementary school setting. Also, I was reminded that even these gifted students might need a little help with simplifying the answer. So let me discuss how I helped these young students discover the answer. I found the ensuing discussion especially enlightening, and so I’m dividing this discussion into several posts.

Here’s a non-standard BINGO board:

Using the free space in the middle, there are four ways of winning the game in four moves:

Horizontally (11-12-13-14)
Vertically (3-8-17-22)
Diagonally (1-7-18-24)
Diagonally (5-9-16-20)

A standard BINGO board has 75 possible numbers (B 1-15, I 16-30, N 31-45, G 46-60, O 61-75). However, the board that I was using with my class (which was being used for pedagogical purposes) only had 44 possibilities. So the solution below assumes these 44 possibilities; the answer for a standard BINGO board is obvious.

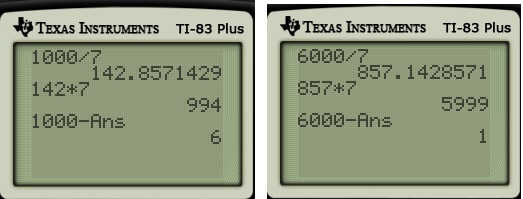
My class quickly decided to start by solving the problem for the horizontal case. I began by asking for the chance that the first number will be on the middle row; after some thought, the class correctly answered $\displaystyle \frac{4}{44}$ .

Next, I asked the chance that the next number would also be on the middle row. To my surprise, this wasn’t automatic for my young but gifted students. They felt that they didn’t know where the first number was, and so they felt like they couldn’t know the chance for the second number. To get them over this conceptual barrier (or so I thought), I asked them to pretend that the first number was 11. Then what would be the odds that the next number fell on the middle row? After some discussion, the class agreed that the answer was $\displaystyle \frac{3}{43}$ .

Once that barrier was cleared, then the class saw that the next two fractions were $\displaystyle \frac{2}{42}$ and $\displaystyle \frac{1}{41}$ . I then explained that, to get the answer for the four consecutive numbers on the middle row, these fractions have to be multiplied:

$\displaystyle \frac{4}{44} \times \frac{3}{43} \times \frac{2}{42} \times \frac{1}{41}$

I didn’t justify why the fractions had to be multiplied; my class just accepted this as the way to combined the fractions to get the answer for all four events happening at once.

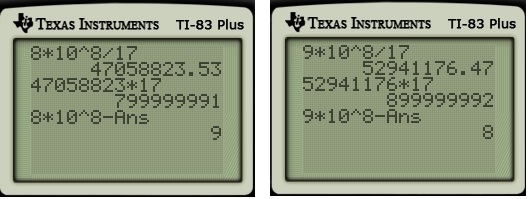
Then I asked about the other three possibilities — the middle column and the two diagonals. The class quickly agreed that the answer should be the same for these other possibilities, and so the final answer should just be four times larger:

$\displaystyle 4 \times \frac{4}{44} \times \frac{3}{43} \times \frac{2}{42} \times \frac{1}{41}$

At this point, I was ready to go on, but then a student asked something like the following:

Shouldn’t the answer be $\displaystyle \frac{1}{44} \times \frac{1}{43} \times \frac{1}{42} \times \frac{1}{41}$ ? I mean, we chose 11 to be the first number so that we can figure out the chance for the second number, and the chance that the first number is 11 is $\displaystyle \frac{1}{41}$ .

Oops. While trying to clear one conceptual hurdle (getting the answer of $\displaystyle \frac{3}{43}$ for the second number), I had inadvertently introduced a second hurdle by making my class wonder if the first number had to be a specific number.

I began by trying to explain that the first number really didn’t have to be 11 after all, but that only seemed to re-introduce the original barrier. Finally, I found an answer that my class found convincing: Yes, the chance that the first number is 11, the second number is 12, the third number is 13, and fourth number is 14 is indeed $\displaystyle \frac{1}{44} \times \frac{1}{43} \times \frac{1}{42} \times \frac{1}{41}$ . But there are other ways that all the numbers could land on the middle row:

The first number could be 12, the second number could be 11, the third number could be 13, and the fourth number could be 14.
Quickly, light dawned, and my class began volunteering other orderings by which all the numbers land in the middle row.
We then enumerated the number of ways that this could happen, and we found that the answer was indeed 24.
I then tied the knot by noting that $4 \times 3 \times 2 \times 1 = 24$ , and so gives another explanation for the numerators in the answer.

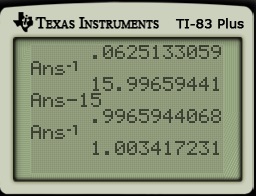
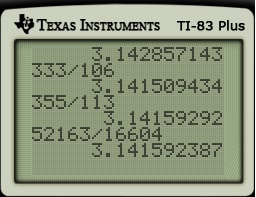
Having found the answer, it was now time to simplify the answer. More on this in tomorrow’s post.

Arithmetic with big numbers (Part 3)

In the previous two posts, we considered the use of base- $10^n$ arithmetic so that a calculator can solve addition and multiplication problems that it ordinarily could not handle. Today, we turn to division. Let’s now consider the decimal representation of $\displaystyle \frac{8}{17}$ .

There’s no obvious repeating pattern. But we know that, since 17 has neither 2 nor 5 as a factor, that there has to be a repeating decimal pattern.

So… what is it?

When I ask this question to my students, I can see their stomachs churning a slow dance of death. They figure that the calculator didn’t give the answer, and so they have to settle for long division by hand.

That’s partially correct.

However, using the ideas presented below, we can perform the long division extracting multiple digits at once. Through clever use of the calculator, we can quickly obtain the full decimal representation even though the calculator can only give ten digits at a time.

Let’s now return to where this series began… the decimal representation of $\displaystyle \frac{1}{7}$ using long division. As shown below, the repeating block has length $6$ , which can be found in a few minutes with enough patience. By the end of this post, we’ll consider a modification of ordinary long division that facilitates the computation of really long repeating blocks.

Because we arrived at a repeated remainder, we know that we have found the repeating block. So we can conclude that $\displaystyle \frac{1}{7} = 0.\overline{142857}$ .

Students are taught long division in elementary school and are so familiar with the procedure that not much thought is given to the logic behind the procedure. The underlying theorem behind long division is typically called the division algorithm. From Wikipedia:

Given two integers $a$ and $b$ , with $b \ne 0$ , there exist unique integers $q$ and $r$ such that $a = bq+r$ and $0 \le r < |b|$, where $|b|$ denotes the absolute value of $b$ .

The number $q$ is typically called the quotient, while the number $r$ is called the remainder.

Repeated application of this theorem is the basis for long division. For the example above:

Step 1.

$10 = 1 \times 7 + 3$ . Dividing by $10$ , $1 = 0.1 \times 7 + 0.3$

Step 2.

$30 = 4 \times 7 + 2$ . Dividing by $100$ , $0.3 = 0.04 \times 7 + 0.02$

Returning to the end of Step 1, we see that

$1 = 0.1 \times 7 + 0.3 = 0.1 \times 7 + 0.04 \times 7 + 0.02 = 0.14 \times 7 + 0.02$

Step 3.

$20 = 2 \times 7 + 6$ . Dividing by $1000$ , $0.02 = 0.002 \times 7 + 0.006$

Returning to the end of Step 2, we see that

$1 = 0.14 \times 7 + 0.02 = 0.14 \times 7 + 0.0002 \times 7 + 0.006 = 0.142 \times 7 + 0.006$

And so on.

By adding an extra zero and using the division algorithm, the digits in the decimal representation are found one at a time. That said, it is possible (with a calculator) to find multiple digits in a single step by adding extra zeroes. For example:

Alternate Step 1.

$1000 = 142 \times 7 + 6$ . Dividing by $1000$ , $1 = 0.142 \times 7 + 0.006$

Alternate Step 2.

$6000 = 587 \times 7 + 1$ . Dividing by $100000$ , $0.006 = 0.000587 \times 7 + 0.000001$

Returning to the end of Alternate Step 1, we see that

$1 = 0.142 \times 7 + 0.006= 0.142 \times 7 + 0.000587\times 7 + 0.000001 = 0.142857 \times 7 + 0.000001$

So, with these two alternate steps, we arrive at a remainder of $1$ and have found the length of the repeating block.

The big catch is that, if $a = 1000$ or $a = 6000$ and $b = 7$ , the appropriate values of $q$ and $r$ have to be found. This can be facilitated with a calculator. The integer part of $1000/7$ and $6000/7$ are the two quotients needed above, and subtraction is used to find the remainders (which must be less than $7$ , of course).

At first blush, it seems silly to use a calculator to find these values of $q$ and $r$ when a calculator could have been used to just find the decimal representation of $1/7$ in the first place. However, the advantage of this method becomes clear when we consider fractions who repeating blocks are longer than 10 digits.

Let’s now return to the question posed at the top of this post: finding the decimal representation of $\displaystyle \frac{8}{17}$ . As noted in Part 6 of this series, the length of the repeating block must be a factor of $\phi(17)$ , where $\phi$ is the Euler toitent function, or the number of integers less than $17$ that are relatively prime with $17$ . Since $17$ is prime, we clearly see that $\phi(17) = 16$ . So we can conclude that the length of the repeating block is a factor of $16$ , or either $1$ , $2$ , $4$ , $8$ , or $16$ .

Here’s the result of the calculator again:

We clearly see from the calculator that the repeating block doesn’t have a length less than or equal to $8$ . By process of elimination, the repeating block must have a length of $16$ digits.

Now we perform the division algorithm to obtain these digits, as before. This can be done in two steps by multiplying by $10^8 = 100,000,000$ .

So, by the same logic used above, we can conclude that

$\displaystyle \frac{8}{17} = 0.\overline{4705882352941176}$

In other words, through clever use of the calculator, the full decimal representation can be quickly found even if the calculator itself returns only ten digits at a time… and had rounded the final $2941176$ of the repeating block up to $3$ .

(Note: While this post continues exploring the unorthodox use of a calculator to handle arithmetic problems, it also appeared in a previous series on the decimal expansions of rational numbers.)

Reflections by a teacher on the Common Core

The implementation of the Common Core has left a lot to be desired, but it’s heartening to see that some teachers have embraced what the Common Core attempts to accomplish. I saw the following first-person person referenced in the Washington Post; the original post can be found at http://www.youngedprofessionals.org/1/post/2014/03/is-the-common-core-working-in-the-classroom.html.

The Common Core State Standards are a reality now for teachers in Maryland and DC, while Virginia is one of six states to omit the standards from their state education approach. YEP-DC asked local educators how the Common Core is playing out in their classroom. Are the standards increasing student understanding or presenting obstacles? What’s changed in pedagogical approach, and how are students are reacting to the shift?

Meredith Rosenberg, fourth-grade teacher

Compare 1/4 and 5/6. This seemingly simple problem is a no-brainer for adults. We know right away that 5/6 is greater than 1/4. But where do you begin with a student who has no conceptual understanding of what a fraction is?

One of the most defining features of the Common Core is how it introduces concepts to students through different modes of comprehension. By the end of a six-week Common Core unit on fractions, my students were talking about, writing about, drawing, and playing with fractions. When they encountered the above problem on a quiz, some students drew a picture, while others found common denominators. A few used a strategy called common numerators, which requires a deep understanding of the denominator of a fraction. One student drew the fractions on a number line. The takeaway: The students in my class were able to compare these fractions in no fewer than five different ways.

The Common Core implementation is not without its challenges. Many standards are vague, and there are only small bits of information coming from the Partnership for the Assessment of Readiness in College and Career (PARCC) on how they are to be tested. The inconsistency with which the standards have been implemented result in the need for highly differentiated classrooms. For example, some of my students came into fourth grade with a solid conceptual understanding of fractions, while others from other schools had no idea what a fraction meant.

However, my school has prioritized Common Core implementation and tackled its challenges with consistent professional development, regular refinement of unit plans, daily lessons and assessments, and an intense focus on the Standards for Mathematical Practice. As a result, my students are thinking critically about numbers every day, and they are becoming accustomed to attacking problems with multiple strategies and assessing the validity of those strategies. The Common Core standards choose depth over breadth, and with appropriate teacher development and support, this leads to much more critical thinking and analysis in the classroom.

Engaging students: Dividing fractions

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Chelsea Hancock. Her topic, from Pre-Algebra: dividing fractions.

Applications (A1)

Students can encounter the division of fractions in a variety of places outside of the classroom. Some of these instances could even happen in your own home! When using fractions, the most common examples include slicing pizza or pie into equal slices. Here is one of those problems:

Assume you have seven-eighths of a whole pizza left. Three of your friends walk into the kitchen and ask for one-fourth of the whole pizza each. If you wanted to share with your friends, will you have enough pizza for each friend to get the amount they want? (Divide 7/8 by 1/4 and see if it’s bigger than three).

$\displaystyle \frac{7/8}{1/4} = \displaystyle \frac{7 \times 4}{8 \times 1} = \displaystyle \frac{28}{8} = 3 \frac{1}{2}$

It is bigger than three, therefore there is, in fact, enough pizza left for all three of your friends to get the amount they wanted.

Other problems might involve finding a fraction of a fraction of a whole. Here is an example of this:

I have a giant cookie jar with 36 cookies in it. My family comes over and eats some of the cookies. If 1/3 of the cookies are eaten and 3/4 of the eaten cookies had frosting, how many of the eaten cookies had frosting? (Multiply 36 by 1/3 to get 12. Then multiply 12 by 3/4).

$\displaystyle 36 \times \frac{1}{3} = \displaystyle \frac{36}{3} =12$

$\displaystyle 12 \times \frac{3}{4} = \displaystyle \frac{12 \times 3}{4} = \frac{36}{4} = 9$ .

Nine of the eaten cookies had frosting.

Curriculum (B2)

In previous mathematics classes, students have obtained a wide variety of skills which can be used when dividing fractions. These skills include the multiplication of whole numbers, the division of whole numbers, and how to reduce fractions to their simplest form. Dividing fractions is an extension of these skills. It can also be said that students already understand what a fraction is. On a separate note, we will discuss how many students relate to fractions and how they think of fractions when confronted with them.

Many students find fractions difficult and intimidating, often freezing when they see a fraction. Involve more than one fraction in a problem and students will get easily frustrated and give up. This can be caused by the way a student perceives fractions. Many students are taught that a fraction is simply part of a bigger whole number. While this is true, many students lose focus on the big picture and get caught up on the fact that a fraction is less than 1 whole unit. In order to help avoid this, teachers could instead try explaining fractions in a slightly different way: a fraction is just a number written like a division problem. The video found at http://www.youtube.com/watch?v=3xwDryouw6o can help to provide a more in-depth explanation about this new perspective on fractions.

By thinking of a fraction as simply a division problem, students automatically incorporate their previous knowledge on dividing whole numbers. When students work through a problem with dividing fractions, they will go through the steps of “keep, change, and flip.” Once they have changed the division symbol to a multiplication symbol and flipped the second fraction, the students will be ready to use their previous knowledge on multiplying whole numbers. After the numerators and denominators are multiplied respectively and the new fraction is obtained, the students must recall previous knowledge on the reduction of fractions to their simplest form.

Technology (E1)

A video can be used to engage students and give them a foundation for dividing fractions. The video I chose, which can be found at http://www.youtube.com/watch?v=uMz4Hause-o, is an excellent example of an acceptable engagement tool. In the video Flocabulary uses music and repetition to describe how to perform the task of dividing fractions. This will help the students be able to recall the information about dividing fractions later on when they need to. Flocabulary explains the process step-by-step and then demonstrates the method in action, using two different fractions to help students understand how it works. Then the video goes on to explain why we flip the second fraction in a division problem, which is vital for ensuring that actual learning is taking place and not simple memorization. Students need to know why they perform certain steps and why the trick works. While the cartoon animations are meant to target a younger audience, this clip is easy to follow and the repetitious nature of the music puts an interesting spin on learning mathematics.

Engaging students: Determining the largest fraction

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Shama Surani. Her topic, from Pre-Algebra: determining which of two fractions is largest if the denominators are unequal.

A2. How could you as a teacher create an activity or project that involves your topic?

An activity that involves students to determine which of two fractions is greatest is called Compare Fractions, which is a two-player math game found at the website http://www.education.com. The objective of the game is to work together to determine who has created the largest fraction. The materials necessary is a deck of cards with the face cards removed, notebook paper, and a pencil. Below are the directions of this game:

Review the concepts of numerator and denominator.
Decide on a dealer and have him/her shuffle the cards.
Divide the deck evenly among the players.
Have the players place their cards face down in a pile in front of them.
To begin playing, have players turn over two cards from their respective decks and place them in front of themselves.
Players can then decide which card they want to be in the numerator and which card they want to be the denominator.
Now the players have to calculate who has the largest fraction. There are a variety ways this can be done. Encourage different methods in determining which fraction is larger. One way is to multiply the numerator and denominator of each fraction by the denominator of the other fraction. For example, with the fractions 5/6 and 4/7, compute 5/6 x 7/7 = 35/42 and 4/7 x 6/6 =24/42. The largest fraction is 35/42 so 5/6 must be greater than 4/7.
The player who has the largest fraction wins all of the cards played in the round. For the instance of a tie (when the both students have equivalent fractions), split the cards evenly among the players.
The game is over when the players have accumulated all of the cards.
Have the players count their cards. Whoever has the most cards, wins.

I believe this activity will be fun for the students because they are creating their own fractions with the cards. Once the students are comfortable with determining which of the two fractions is greatest, the teacher can start timing the students if he/she wants to.

B2. How does this topic extend what your students should have learned in previous courses?

In previous courses, students should have learned how to draw a number line and determine where on the number line two natural numbers are located. They would have known how to compare numbers or order the numbers from least to greatest or greatest to least. Then, the students were exposed to fractions as being a part of whole, and being called rational numbers. This concept is then extended to ordering fractions with equal denominators with visual diagrams and using the number line. In a visual illustration, the students can be exposed to two circles of the same size but divided into the same amount of sections. For example, both circles can be divided into four equal sections, but one can have two sections filled in while the other has three sections filled in. Students then can determine which circle is larger. In this case, the circle with three sections filled in is larger. Then this concept is extended to be written in fraction format where the first circle is 2/4 and the other circle is 3/4. When the students have fractions with equal denominators, they look at the numerator to see which fraction is larger or smaller. Determining which of two fractions is greatest if the denominators are not equal extends off this previous concept. The best way is to show the students visually how different shapes such as a square or a circle can be divided equally into different sections. For example, the first circle might be divided into four sections with three sections shaded while the other circle can be divided into eight sections with seven shaded. In fraction form, the first circle is 3/4 while the other circle is 7/8. Here the students will notice that the denominators are different but by looking at the shaded circles, they can see that 7/8 is larger than 3/4.

E1. How can technology be used to effectively engage students in this topic?

Technology is increasing day by day, and in many respects, technology can be the tool for aiding learning in the classrooms. One way that technology can be used to effectively engage students in determining which of two fractions is greatest when the denominators are unequal by playing simple online games. Since several schools are distributing i-Pads to their students, I have found an i-Pad application called “Fraction Monkeys” that the students can download for free for this lesson. This application is a wonderful tool in demonstrating how fractions with same or different denominators are located on the number line. The objective of this game is that a monkey with a fraction will appear on the screen. The student will have to place the monkey correctly on the number line. Sometimes the card the monkey holds up is in reduced form, so the student will have to think about how that reduced form relates to the number line.

For example, below is a picture of a number line with the denominator being 16. When the student is finished placing the monkeys on the correct location, they will notice that the monkeys were placed differently depending on what fraction they received.

By providing the students with a guided worksheet, the students will be able to compare which fractions are greater and which fractions is less than the other by viewing the number line. For example:

$\displaystyle \frac{7}{8} ~~ ? ~~ \frac{3}{4}$

The student will answer that 7/8 is greater than 3/4 since 3/4 comes before 7/8 on the number line. I believe this activity will help the students conceptualize how to compare fractions. In addition, in case when the student incorrectly places a monkey on the number line, a hint with little squares pops up where the student can visually see how their fraction relates to the number line. Below is a picture demonstrating this:

Another computer game that involves comparing fractions is named “Balloon Pop Math.” This is also a good resource to use because it shows balloons with fractions with a visual of a circle divided in equal sections. The idea of this game is to pop the balloon with the smallest fraction to the largest fraction with different denominators. Below is a picture from the game demonstrating the fractions 7/8 and 4/5. The students will be able to see that 4/5 is less than 7/8 by looking at the circle so the student will pop the balloon that contains 4/5. This game is also wonderful to use because it contains three levels. The first level allows the students to compare two fractions. The next one allows the student to compare three fractions, and the last level allows the students to compare four fractions. This will be a good engagement activity to allow the students to do before teaching about how to compare which two fractions is greater than the other.

References:

http://www.fractionmonkeys.co.uk/activity/

http://www.sheppardsoftware.com/mathgames/fractions/Balloons_fractions1.htm

http://www.education.com/activity/article/capture-that-fraction/

Trivia question for the day

Which is worth more: a pound of dimes, a pound of quarters, or a pound of dollars?

Rather than spoiling the fun for my readers, I’ll just leave this one unanswered and let you think about it. Feel free to Google for help.

Why do we still require students to rationalize denominators?

Which answer is simplified: $\displaystyle \frac{1}{2 \sqrt{2}}$ or $\displaystyle \frac{ \sqrt{2} }{4}$ ? From example, here’s a simple problem from trigonometry:

Suppose $\theta$ is an acute angle so that $\sin \theta = \displaystyle \frac{1}{3}$ . Find $\tan \theta$ .

To solve, we make a right triangle whose side opposite of $\theta$ has length $1$ and hypotenuse with length $3$ . The adjacent side has length $\sqrt{3^2 - 1^2} = \sqrt{8} = 2\sqrt{2}$ . Therefore,

$\tan \theta = \displaystyle \frac{ \hbox{Opposite} }{ \hbox{Adjacent} } = \displaystyle \frac{1}{2 \sqrt{2}}$

This is the correct answer, and it could be plugged into a calculator to obtain a decimal approximation. However, in my experience, it seems that most students are taught that this answer is not yet simplified, and that they must rationalize the denominator to get the “correct” answer:

$\tan \theta = \displaystyle \frac{1}{2 \sqrt{2}} \cdot \frac{ \sqrt{2} }{ \sqrt{2} } = \displaystyle \frac{ \sqrt{2} }{4}$

Of course, this is equivalent to the first answer. So my question is philosophical: why are students taught that the first answer isn’t simplified but the second is? Stated another way, why is a square root in the numerator so much more preferable than a square root in the denominator?

Feel free to correct me if I’m wrong, but it seems to me that rationalizing denominators is a vestige of an era before cheap pocket calculators. Let’s go back in time to an era before pocket calculators… say, 1927, when The Jazz Singer was just released and stars of silent films, like Don Lockwood, were trying to figure out how to act in a talking movie.

Before cheap pocket calculators, how would someone find $\displaystyle \frac{1}{2 \sqrt{2}} ~~$ or $~~ \displaystyle \frac{ \sqrt{2} }{4}$ to nine decimal places? Clearly, the first step is finding $\sqrt{2}$ by hand, which I discussed in a previous post. So these expressions reduce to

$\displaystyle \frac{1}{2 (1.41421356\dots)}$ or $\displaystyle \frac{1.41421356\dots}{4}$

Next comes the step of dividing. If you don’t have a calculator and had to use long division, which would rather do: divide by $4$ or divide by $2.82842712\dots$ ?

Clearly, long division with $4$ is easier.

It seems to me that ease of computation was the reason that rationalizing denominators was required of students in previous generations. So I’m a little bemused why rationalizing denominators is still required of students now that cheap calculators are so prevalent.

Lest I be misunderstood, I absolutely believe that all students should be able to convert $\displaystyle \frac{1}{2 \sqrt{2}}$ into $\displaystyle \frac{ \sqrt{2} }{4}$ . But I see no compelling reason why the “simplified” answer to the above trigonometry problem should be the second answer and not the first.

Continued fractions and pi

I suggest the following activity for bright middle-school students who think that they know everything that there is to know about fractions.

The approximation to $\pi$ that is most commonly taught to students is $\displaystyle \frac{22}{7}$ . As I’ll discuss, this is the closest rational number to $\pi$ using a denominator less than $100$ . However, it is possible to obtain closer rational approximations to $\pi$ using larger numbers. Indeed, the ancient Chinese mathematicians were superior to the ancient Greeks in this regard, as they developed the approximation

$\pi \approx \displaystyle \frac{355}{133}$

It turns out that this is the best rational approximation to $\pi$ using a denominator less than $16,000$ . In other words, $\displaystyle \frac{355}{133}$ is the best approximation to $\pi$ using a reasonably simple rational number.

Step 1. To begin, let’s find $\pi$ with a calculator. Then let’s now subtract $3$ and then find the inverse.

This calculation has shown that

$\pi = \displaystyle 3 + \frac{1}{7.0625133\dots}$

If we ignore the $0.0625133$ , we obtain the usual approximation

$\pi \approx \displaystyle 3 + \frac{1}{7} = \frac{22}{7}$

Step 2. However, there’s no reason to stop with one reciprocal, and this might give us some even better approximations. Let’s subtract $7$ from the current denominator and find the reciprocal of the difference.

At this point, we have shown that

$\pi = \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15.9965944\dots}}$

If we round the final denominator down to $15$ , we obtain the approximation

$\pi \approx \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15}}$

$\pi \approx \displaystyle 3 + \frac{1}{~~~\displaystyle \frac{106}{15}~~~}$

$\pi \approx \displaystyle 3 + \frac{15}{106}$

$\pi \approx \displaystyle \frac{333}{106}$

Step 3. Continuing with the next denominator, we subtract $15$ and take the reciprocal again.

At this point, we have shown that

$\pi = \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15 + \displaystyle \frac{1}{1.00341723\dots}}}$

If we round the final denominator down to $1$ , we obtain the approximation

$\pi \approx \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{16}}$

$\pi \approx \displaystyle 3 + \frac{1}{~~~\displaystyle \frac{113}{16}~~~}$

$\pi \approx \displaystyle 3 + \frac{16}{113}$

$\pi \approx \displaystyle \frac{355}{113}$

Step 4. Let me show one more step.

At this point, we have shown that

$\pi = \displaystyle 3 + \frac{1}{7 + \displaystyle\frac{1}{15 + \displaystyle \frac{1}{1 + \displaystyle \frac{1}{292.634598\dots}}}}$

If we round the final denominator down to $292$ , we (eventually) obtain the approximation

$\pi \approx \displaystyle \frac{52163}{16604}$

The calculations above are the initial steps in finding the continued fraction representation of $\pi$ . A full treatment of continued fractions is well outside the scope of a single blog post. Instead, I’ll refer the interested reader to the good write-ups at MathWorld (http://mathworld.wolfram.com/ContinuedFraction.html) and Wikipedia (http://en.wikipedia.org/wiki/Continued_fraction) as well as the references therein.

But I would like to point out one important property of the convergents that we found above, which were

$\displaystyle \frac{22}{7}, \frac{333}{106}, \frac{355}{113}, ~ \hbox{and} ~ \frac{52163}{16604}$

All of these fractions are pretty close to $\pi$ , as shown below. (The first decimal below is the result for $22/7$ .)

In fact, these are the first terms in a sequence of best possible rational approximations to $\pi$ up to the given denominator. In other words:

$\displaystyle \frac{22}{7}$ is the best rational approximation to $\pi$ using a denominator less than $106$. In other words, no integer over $8$ will be any closer to $\pi$ than $\displaystyle \frac{22}{7}$ . No integer over $9$ will be any closer to $\pi$ than $\displaystyle \frac{22}{7}$ . And so on, all the way up to denominators of $105$ . Small wonder that we usually teach children the approximation $\pi \approx \displaystyle \frac{22}{7}$ .
Once we reach $106$ , the fraction $\displaystyle \frac{323}{106}$ is the best rational approximation to $\pi$ using a denominator less than $113$ .
Then $\displaystyle \frac{355}{113}$ is the best rational approximation to $\pi$ using a denominator less than $16604$ .

As noted above, the ancient Chinese mathematicians were superior to the ancient Greeks in this regard, as they were able to develop the approximation $\pi \approx \displaystyle \frac{355}{113}$ . For example, Archimedes was able to establish that

$3\frac{10}{71} < \pi < 3\frac{1}{7}$

Why does 0.999… = 1? (Part 4)

In this series, I discuss some ways of convincing students that $0.999\dots = 1$ and that, more generally, a real number may have more than one decimal representation even though a decimal representation corresponds to only one real number. This can be a major conceptual barrier for even bright students to overcome. I have met a few math majors within a semester of graduating — that is, they weren’t dummies — who could recite all of these ways and were perhaps logically convinced but remained psychologically unconvinced.

Method #5. This is a proof by contradiction; however, I think it should be convincing to a middle-school student who’s comfortable with decimal representations. Also, perhaps unlike Methods #1-4, this argument really gets to the heart of the matter: there can’t be a number in between $0.999\dots$ and $1$ , and so the two numbers have to be equal.

In the proof below, I’m deliberating avoiding the explicit use of algebra (say, letting $x$ be the midpoint) to make the proof accessible to pre-algebra students.

Suppose that $0.999\dots < 1$ . Then the midpoint of $0.999\dots$ and $1$ has to be strictly greater than $0.999\dots$ , since

$\displaystyle \frac{0.999\dots + 1}{2} > \displaystyle \frac{0.999\dots + 0.999\dots}{2} = 0.999\dots$

Similarly, the midpoint is strictly less than $1$ :

$\displaystyle \frac{0.999\dots + 1}{2} < \displaystyle \frac{1 +1}{2} =1$

(For the sake of convincing middle-school students, a number line with three tick marks — for $0.999\dots$ , $1$ , and the midpoint — might be more believable than the above inequalities.)

So what is the decimal representation of the midpoint? Since the midpoint is less than $1$ , the decimal representation has to be $0.\hbox{something}$ Furthermore, the midpoint does not equal $0.999\dots$ . That means, somewhere in the decimal representation of the midpoint, there’s a digit that’s not equal to $9$ . In other words, the midpoint has to have one of the following 9 forms:

midpoint = $0.999\dots 990 \, \_ \, \_ \dots$

midpoint = $0.999\dots 991 \, \_ \, \_ \dots$

midpoint = $0.999\dots 992 \, \_ \, \_ \dots$

midpoint = $0.999\dots 993 \, \_ \, \_ \dots$

midpoint = $0.999\dots 994 \, \_ \, \_ \dots$

midpoint = $0.999\dots 995 \, \_ \, \_ \dots$

midpoint = $0.999\dots 996 \, \_ \, \_ \dots$

midpoint = $0.999\dots 997 \, \_ \, \_ \dots$

midpoint = $0.999\dots 998 \, \_ \, \_ \dots$

In any event, $9$ is the largest digit. That means that, no matter what, the midpoint is less than $0.999\dots$ , contradicting the fact that the midpoint is larger than $0.999\dots$ (if $0.999\dots < 1$ ).

Why does 0.999… = 1? (Part 3)

Method #4. This is a direct method using the formula for an infinite geometric series… and hence will only be convincing to students if they’re comfortable with using this formula. By definition,

$0.999\dots = \displaystyle \frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \dots$

This is an infinite geometric series. Its first term is $\displaystyle \frac{9}{10}$ , and the common ratio needed to go from one term to the next term is $\displaystyle \frac{1}{10}$ . Therefore,

$0.999\dots = \displaystyle \frac{ \displaystyle \frac{9}{10}}{ \quad \displaystyle 1 - \frac{1}{10} \quad}$

$0.999\dots = \displaystyle \frac{ \displaystyle \frac{9}{10}}{ \quad \displaystyle \frac{9}{10} \quad}$

$0.999\dots = 1$