Exponential growth and decay (Part 2): Paying off credit-card debt

The following problem in differential equations has a very practical application for anyone who has either (1) taken out a loan to buy a house or a car or (2) is trying to pay off credit card debt. To my surprise, most math majors haven’t thought through the obvious applications of exponential functions as a means of engaging their future students, even though it is directly pertinent to their lives (both the students’ and the teachers’).

You have a balance of $2,000 on your credit card. Interest is compounded continuously with a relative rate of growth of 25% per year. If you pay the minimum amount of $50 per month (or $600 per year), how long will it take for the balance to be paid?

In this post, I present the actual solution of this problem. In tomorrow’s post, I’ll give some pedagogical thoughts about how this problem, and other similar problems inspired by financial considerations, could fit into a Precalculus course.

Let’s treat this problem as a differential equation (though it could also be considered as a first-order difference equation… more on that later). Let $A(t)$ be the amount of money on the credit card after $t$ years. Then there are two competing forces on the amount of money that will be owed in the future:

The effect of compound interest, which will increase the amount owed by $0.25 A(t)$ per year.
The amount that’s paid off each year, which will decrease the amount owed by $\$600$ per year.

Combining, we obtain the differential equation

$\displaystyle \frac{dA}{dt} = 0.25 A - 600$

There are a variety of techniques by which this differential equation can be solved. One technique is separation of variables, thus pretending that $dA/dt$ is actually a fraction. (In the derivation below, I will be a little sloppy with the arbitrary constant of integration for the sake of simplicity.)

$\displaystyle \frac{dA}{0.25 A - 600} = dt$

$\displaystyle \int \frac{dA}{0.25 A - 600} = \displaystyle \int dt$

$\displaystyle 4 \int \frac{0.25 dA}{0.25 A - 600} = \displaystyle \int dt$

$4 \ln |0.25A - 600| = t + C$

$\ln |0.25A - 600| = 0.25 t + C$

$|0.25A - 600| = e^{0.25 t + C}$

$|0.25 A - 600| = C e^{0.25t}$

$0.25A - 600 = C e^{0.25t}$

$0.25 A = 600 + C e^{0.25t}$

$A = 2400 + C e^{0.25t}$

To solve for the missing constant $C$ , we use the initial condition $A(0) = 2000$ :

$A(0) = 2400 + C e^0$

$2000 = 2400 + C$

$-400 = C$

We thus conclude that the amount of money owed after $t$ years is

$A(t) = 2400 - 400 e^{0.25t}$

To determine when the amount of the credit card will be reduced to $0, we see $A(t) = 0$ and solve for $t$ :

$0 = 2400 - 400 e^{0.25 t}$

$400 e^{0.25 t} = 2400$

$e^{0.25t} = 6$

$0.25t = \ln 6$

$t = 4 \ln 6$

$t \approx 7.2 \hbox{~years}$

In tomorrow’s post, I’ll give some pedagogical thoughts about this problem and similar problems.

Exponential growth and decay (Part 1): Phrasing of homework questions

I just completed a series of posts concerning the different definitions of the number $e$ . As part of this series, we considered the formula for continuous compound interest

$A = Pe^{rt}$

Indeed, this formula can be applied to other phenomena besides the accumulation of money. Unfortunately, as they appear in Precalculus textbooks, the wording of questions involving exponential growth or decay can be either really awkward or mathematically imprecise (or both). Here’s a sampling of problems that I’ve collected from various sources:

One thousand bacteria on a petri dish are placed in an incubator, encouraging a relative rate of growth of 10% per hour. How many bacteria will there be in two days?

This is mathematically precise, as it relates to the differential equation $A'(t) = r A(t)$ with solution $A = P e^{rt}$ . The meaning of the value of $r$ is clear from dimensional analysis: the units of $A'(t)$ are $\hbox{bacteria}/ \hbox{hour}$ , while the units of $A(t)$ are $\hbox{bacteria}$ . Therefore, the units of $r$ must be $\hbox{hour}^{-1}$ . So saying that there’s a “relative rate of growth of 10% per hour” makes total sense.

Of course, when Precalculus students are solving this problem, they have no idea about what a differential equation is, making the word relative seem superfluous to the problem.

A sum of $5000 is invested at an interest rate of 9% per year. Find the time required for the money to double if the interest is compounded continuously.

What the problem is trying to say is “Let $r = 0.09$ .” But this is a horrible way to write this in ordinary English! After all, if we plug $r = 0.09$ and $t = 1$ into the formula, we obtain

$A = P e^{0.09 \times 1} \approx 1.09417P$

So it would appear that the interest rate after one year is about 9.417%, and not 9%.

Indeed, if we read the problem at face value that the interest rate is 9% per year, then it stands to reason that, after one year, we have

$P(1.09) = P e^{r \cdot 1}$

$1.09 = e^r$

$\ln 1.09 = r$

In a nutshell, saying that there is “an interest rate of 9% per year” can easily be interpreted to mean that the annual percentage rate is 9% year, and this can be a conceptual barrier for literally-minded students.

I don’t have a good solution for this impasse between ordinary English and giving clear directions to students about what numbers should be used in the formula. But I do think that it’s important for teachers to be aware of this possible misunderstanding as students read their homework questions.

Different definitions of e (Part 6): Continuous compound interest

In this series of posts, I consider how two different definitions of the number $e$ are related to each other. The number $e$ is usually introduced at two different places in the mathematics curriculum:

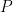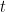Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after 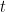$t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

These two definitions appear to be very, very different. One deals with making money. The other deals with the area under a hyperbola. Amazingly, these two definitions are related to each other. In this series of posts, I’ll discuss the connection between the two.

I should say at the outset that the second definition is usually considered the true definition of $e$ . However, compound interest usually appears earlier in the mathematics curriculum than definite integrals, and so an informal definition of $e$ is given at that stage of the curriculum.

In yesterday’s post, I presented an informal derivation of the continuous compound interest formula $A = Pe^{rt}$ from the discrete compound interest formula $A = \displaystyle P \left( 1 + \frac{r}{n} \right)^{nt}$ . In today’s post, I’d like to give the more formal derivation using calculus.

What does it mean for something to compound continuously? In a nutshell, the rate at which the money increases should be proportional to the amount currently present. In other words, $\$10,000$ should earn ten times as much interest as $\$1,000$ . Since $A'(t)$ is the rate at which the money increases and $A(t)$ is the current amount, that means

$A'(t) = r A(t)$

for some constant of proportionality $r$ . This is a differential equation which can be solved using standard techniques. We divide both sides by $A(t)$ and then integrate:

$\displaystyle \frac{A'(t)}{A(t)} = r$

$\displaystyle \int \frac{A'(t)}{A(t)} dt = \int r dt$

$\ln |A(t)| = r t + C$

$|A(t)| = e^{rt+C} = e^rt e^C = C_1 e^{rt}$

$A(t) = \pm C_1 e^{rt}$

$A(t) = C_2 e^{rt}$

(Technically, a better solution would use an integrating factor [see also MathWorld], but I find that the above derivation is much more convincing to students who are a few semesters removed from a formal course in differential equations.) When presenting this in class, I’ll sometimes lazily write $C$ in place of $C_1$ , with the understanding that $e$ to an arbitrary constant is just an arbitrary positive constant. Also, on the last line, plus or minus an arbitrary constant is just an arbitrary constant (which I’ll usually write as $C$ instead of $C_2$ ).

To solve for the missing constant $C_2$ , we use the initial condition $A(0) = P$ :

$A(0) = C_2 e^{r\cdot 0}$

$P = C_2 \cdot 1$

$P = C_2$

Replacing $C_2$ by $P$ , we have arrived at the continuous compound interest formula $A(t) = Pe^{rt}$ .

Different definitions of e (Part 5): Continuous compound interest

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

$\displaystyle \left(1 + \frac{1}{n} \right) \to e \qquad$ as $\qquad n \to \infty$ .

We are now in position to give an informal derivation of the continuous compound interest formula. Though this derivation is informal, I have found it to be very convincing for my Precalculus students (as well as to my class of future high school teachers).

The basic idea is to rewrite the discrete compound interest formula so that it contains a term like $\displaystyle \frac{1}{\hbox{something}}$ instead of $\displaystyle \frac{r}{\hbox{something}}$ . In this way, we can think like an MIT freshman and reduce to previous work.

To this end, let $n = mr$ . Then the discrete compound interest formula becomes

$A = P\displaystyle \left( 1 + \frac{r}{n} \right)^{nt}$

$A = P\displaystyle \left( 1 + \frac{r}{rm} \right)^{rmt}$

$A = P\displaystyle \left( 1 + \frac{1}{m} \right)^{mrt}$

$A = P\displaystyle \left[ \left( 1 + \frac{1}{m} \right)^m \right]^{rt}$

Inside of the brackets is our familiar friend $\displaystyle \left( 1 + \frac{1}{m} \right)^m$ , except that the name of the variable has changed from $n$ to $m$ . But that’s no big deal: as $n$ tends to infinity, then $m$ does as well since $m = n/r$ and both $n$ and $r$ are positive. Therefore, as interest is compounded more frequently, we have replace the thing inside the brackets with the number $e$ . This leads us to the formula for continuous compound interest:

$A =P e^{rt}$

Again, my experience is that college students have no conceptual understanding of this formula or even a memory of seeing it derived once upon a time. They remember is it as coming out of nowhere, as a number in a formula or as a button on a calculator. It really shouldn’t be this way. The above calculation is perhaps a harder sell to high school students that the other calculations that I’ve posted in this series, but I firmly believe that this explanation is within the grasp of good students at the time that they take Algebra II and Precalculus.
Of course, the above derivation is highly informal. For starters, it rests upon the limit

$\displaystyle \lim_{n \to \infty} \left(1 + \frac{1}{n} \right)^n = e$ ,

which cannot be formally proven using only the tools of Algebra II and Precalculus. Second, the above computation rests upon the continuity of the function $A(x) = P x^{rt}$ , so that we can simply replace $\displaystyle \left( 1 + \frac{1}{m} \right)^m$ with its limit $e$ . My experience is that students are completely comfortable making this substitution, even though professional mathematicians realize that interchanging limits requires continuity.

So, mathematically speaking, the above argument should not be considered a proper derivation of the continuous compound interest formula. Still, I have found that the above argument to be quite convincing to Algebra II and Precalculus students, appropriate to their current level of mathematical development.

Different definitions of e (Part 4): Continuous compound interest

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

At this point in the exposition, I have justified the formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ for computing the value of an investment when interest is compounded $n$ times a year. We have also seen that $A$ increases as $n$ increases, but that $A$ appears to level off as $n$ gets very large. This observation forms the basis for the continuous compound interest formula $A = P e^{rt}$ .

To begin, let’s consider plug in variables to make the compound interest formula as simple as possible. Let’s start with 1 dollar (so that $P = 1$ ) that earns 100% interest (so that $r = 1$ ) for one year (so that $t = 1$ ). This isn’t financially realistic, of course, but let’s run with it. Then the compound interest formula becomes

$A = \displaystyle \left( 1 + \frac{1}{n} \right)^n$

As before, let’s see what happens as $n$ increases. As before, I’ll plug numbers into a calculator in real time, asking my students to use their calculators along with me.

If $n = 1$ , then $A = (1+1)^1 = 2$ . I’ll usually double-check with my class to make sure that they believe this answer… that $1 compounded once at 100% interest results in $2.
If $n = 2$ , then $A = (1.5)^2 = 2.25$ .
If $n = 4$ , then $A = (1.25)^4 \approx 2.441$ .
If $n = 10$ , then $A = (1.1)^{10} \approx 2.593$ .
If $n = 1000$ , then $A = (1.001)^{1000} \approx 2.71692$
If $n = 1,000,000$ , then $A = (1.000001)^{1000000} \approx 2.71828$

As before, the final amount $A$ appears to be increasing toward something. That something is defined to be the number $e$ . So, as $n$ tends toward infinity, we’ll define the limiting value to be the number $e$ .

In my experience, college students have no memory of learning how they first saw the number $e$ when they were in high school. They remember is it as coming out of nowhere, as a number in a formula or as a button on a calculator. It really shouldn’t be this way. The above calculation is a natural consequence of the discrete compound interest formula, which makes the appearance of the number $e$ to be a bit more natural.

Of course, this “definition” of the number $e$ is highly informal. What we’re really claiming is

$\displaystyle \lim_{n \to \infty} \left(1 + \frac{1}{n} \right)^n = e$ .

At this point in the mathematical curriculum, students only have the haziest notion of what a limit actually means, let alone the more formal treatment that’s presented in calculus… not to mention a proper $\delta-\epsilon$ treatment of limit in an honors calculus class or in real analysis. So, mathematically speaking, the above argument should not be considered a proper definition of the number $e$ , but a working definition so that high school students can get comfortable with the number $e$ before seeing it again in their future mathematical courses.

Different definitions of e (Part 3): Discrete compound interest

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

At this point in the exposition, I have justified the formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ for computing the value of an investment when interest is compounded $n$ times a year. In tomorrow’s post, I’ll discuss how the above formula naturally leads to the formula $A = P e^{rt}$ when interest is continuously compounded.

The bridge between these two formulas is considering increasing values of $n$ . So far in the presentation, we have considered an investment of $1000 making 4% interest for 2 years. In the first post of this series, we made the following computations:

1. If interest is compounded annually ( $n = 1$ ), then $A = \$1000(1.04)^2 = \$1081.60$ .

2. If interest i compounded semiannually ( $n = 2$ ), then $A = \$1000(1.02)^4 \approx \$1082.43$ .

3. If interest is compounded quarterly ( $n = 4$ ), then $A = \$1000(1.01)^8 \approx \$1082.86$ .

So I ask my class, “What happens to the final amount as interest is compounded more frequently?” They easily observe that the final amount increases somewhat. A natural question, then, is to find how much it can increase. So let’s make the compounding more frequent and let’s see what happens.

4. Daily: ( $n = 365$ ). Then $A = \$1000 \displaystyle \left( 1 + \frac{0.04}{365} \right)^{730} \approx \$1083.28$ .

5. About twice a minute ( $n = 1,000,000$ ): Then $A = \$1000 \displaystyle \left( 1 + \frac{0.04}{1,000,000} \right)^{2,000,000} \approx \$1083.29$ .

Of course, I perform all of these calculations in real time on a calculator so that students can follow along:

Students quickly observe that the final amount continues to increase as $n$ increases. However, the final amount appears to be leveling off… we can’t make the final amount arbitrarily large just by compounding the interest more frequently.

This provides a natural bridge to continuous compound interest, the topic of tomorrow’s post.

I’ll also note parenthetically that this is why financial institutions are required to disclose the annual percentage rate of a loan (among other things). Otherwise, banks could get away with declaring “Only 2% interest monthly!!” That sounds like 24% annual interest. However, $(1.02)^{12} \approx 1.26824$ , and so the annual percentage rate would really be 26.824%.

Different definitions of e (Part 2): Discrete compound interest

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

In yesterday’s post, I used a numerical example to justify the compound interest formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ when interest is compounded $n$ times a year. In a couple of days, I’ll discuss how the above formula naturally leads to the formula $A = P e^{rt}$ when interest is continuously compounded. Today, I’d like to give some pedagogical thoughts about both formulas.

The mathematics in yesterday’s post was pretty straightforward: apply the simple interest formula $I = P r t$ a few times and see if a pattern can be developed. However, my observation is that college students have no memory of being taught how the compound interest formula $A = P \displaystyle \left( 1 + \frac{r}{n} \right)^{nt}$ can be seen as a natural consequence of the simple interest formula. In other words, they’d just use the compound interest formula without having any conceptual understanding of where the formula came from.

For my math majors who aspire to become secondary teachers in the future, I’ll make my observation that there’s absolutely no reason why students couldn’t discover this formula on their own similar to the outline above. Doubtlessly, it would take more time that I use in my college class… I can usually cover the points in yesterday’s post in about 10 minutes or less, even allowing for students to pause and interject the next step of the calculation. So while the pace would be slower for a class of high school students, the mathematical ideas are simple enough to be understood by high school students.

Different definitions of e (Part 1): Discrete compound interest

In the previous series of posts, I consider how two different definitions of a logarithmic function are actually related to each other. In this series of posts, I consider how two different definitions of the number $e$ are related to each other.

The number $e$ is usually introduced at two different places in the mathematics curriculum:

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

I begin this series of posts with a justification for the compound interest formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ when interest is compounded $n$ times a year. My experience is that most math majors are familiar with this formula from their high school experience but have absolutely no idea about why it is true, and so the presentation below fills in a major hole in their preparation to become secondary teachers themselves.

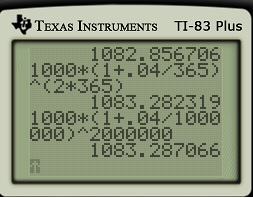
In the near future, I’ll discuss how the above formula naturally leads to the formula 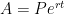$A = P e^{rt}$ when interest is continuously compounded.

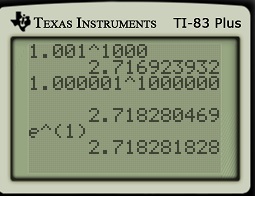
I start with a sequence of numerical examples.

A. Suppose that you invest $1,000 at 4% interest for 2 years. (At the time of this writing, a fixed interest rate of 4% is almost mythological, but let’s leave that aside for the sake of the problem.) How much money do you have if the money is compounded annually? Here are the brute force steps. (To make the presentation less dry, I make sure that my students are volunteering each answer before proceeding to the next step.)

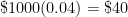Amount of interest earned in Year 1 = $\$1000(0.04) = \$40$ .
Total amount of money after Year 1 = $\$1000 + \$40 = \$1040$ .
Amount of interest earned in Year 2 = $\$1040(0.04) = \$41.60$ .
Total amount of money earned in Year 2 = $\$1040 + \$41.60 = \$1081.60$ .

B. Let’s repeat the above problem, except this time the 4% interest is compounded twice a year. In other words, 2% interest is applied every six months.

Amount of interest earned in first six months = $\$1000(0.02) = \$20$ .
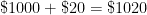Total amount of money after first six months = $\$1000 + \$20 = \$1020$ .
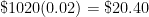Amount of interest earned in second six months = $\$1020(0.02) = \$20.40$ .
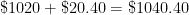Total amount of money earned after second six months = $\$1020 + \$20.40 = \$1040.40$ .

At this point, I’ll make a big production about how much work this is, and we’re only halfway done with this calculation! So, I’ll rhetorically ask my class, is there an easier way to do this? Let’s take a look back at the first calculation, adding some observations.

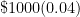Amount of interest earned in Year 1 = $\$1000(0.04)$ .
Total amount of money after Year 1 = $\$1000 + \$1000(0.04) = \$1000(1 + 0.04) = \$1040$ .
Amount of interest earned in Year 2 = $\$1040(0.04)$ .
Total amount of money earned in Year 2 = $\$1040 + \$1040(0.04) = \$1040(1 + 0.04) = \$1000 (1+0.04)(1+0.04)$

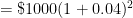$= \$1000(1+0.04)^2$ .

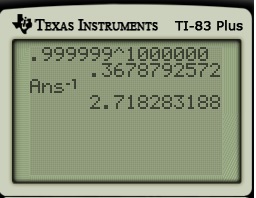
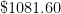Then I’ll check with a calculator to confirm that $\$1000(1+0.04)^2$ is indeed equal to $\$1081.60$ .

Let’s now return to the problem when the 4% interest is compounded twice a year. We’re only halfway through the calculation, but let’s recapitulate what we’ve done so far. Since this is very similar to the above work, students usually can produce the logic very quickly.

Amount of interest earned in first six months = $\$1000(0.02)$ .
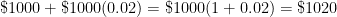Total amount of money after first six months = $\$1000 + \$1000(0.02) = \$1000(1+0.02) = \$1020$ .
Amount of interest earned in second six months = $\$1020(0.02)$ .
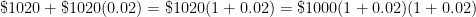Total amount of money earned after second six months = $\$1020 + \$1020(0.02) = \$1020(1 + 0.02) = \$1000(1+0.02)(1+0.02)$ .

$= \$1000(1+0.02)^2$ .

At this point, I’ll ask my class what they think how much money will accumulate after two years. Invariably, they guess the correct answer of $latex $1000(1+0.02)^4$. If my class seems to get it, I usually will just accept this as the correct answer without explicitly running through steps 5 through 8 to get to the end of the fourth six weeks.

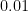C. What is the money makes 4% interest compounded four times a year for 2 years? By this point, my students can usually guess the answer: $A = 1000(1.01)^8$ . The $0.01$ comes from dividing the 4% into four parts. The 8 comes from the number of compounding periods over 2 years.

D. By this point, we have pretty much arrived at the compound interest formula: $A = P \displaystyle \left(1 + \frac{r}{n} \right)^{nt}$ . The above argument justifies the formula; the actual proof of the formula is very similar to the above numerical examples, and so I don’t use class time to formally prove it.

Tomorrow, I’ll give some pedagogical thoughts about these computations.

A surprising appearance of e

Here’s a simple probability problem that should be accessible to high school students who have learned the Multiplication Rule:

Suppose that you play the lottery every day for about 20 years. Each time you play, the chance that you win is $1$ chance in $1000$ . What is the probability that, after playing $1000$ times, you never win?

This is a straightforward application of the Multiplication Rule from probability. The chance of not winning on any one play is $0.999$ . Therefore, the chance of not winning $1000$ consecutive times is $(0.999)^{1000}$ , which we can approximate with a calculator.

Well, that was easy enough. Now, just for the fun of it, let’s find the reciprocal of this answer.

Hmmm. Two point seven one. Where have I seen that before? Hmmm… Nah, it couldn’t be that.

What if we changed the number $1000$ in the above problem to $1,000,000$ ? Then the probability would be $(0.999999)^{1000000}$ .

There’s no denying it now… it looks like the reciprocal is approximately $e$ , so that the probability of never winning for both problems is approximately $1/e$ .

Why is this happening? I offer a thought bubble if you’d like to think about this before proceeding to the answer.

The above calculations are numerical examples that demonstrate the limit

$\displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n = e^x$

In particular, for the special case when $n = -1$ , we find

$\displaystyle \lim_{n \to \infty} \left(1 - \frac{1}{n}\right)^n = e^{-1} = \displaystyle \frac{1}{e}$

The first limit can be proved using L’Hopital’s Rule. By continuity of the function $f(x) = \ln x$ , we have

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \ln \left[ \left(1 + \frac{x}{n}\right)^n \right]$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} n \ln \left(1 + \frac{x}{n}\right)$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \frac{ \displaystyle \ln \left(1 + \frac{x}{n}\right)}{\displaystyle \frac{1}{n}}$

The right-hand side has the form $\infty/\infty$ as $n \to \infty$ , and so we may use L’Hopital’s rule, differentiating both the numerator and the denominator with respect to $n$ .

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \frac{ \displaystyle \frac{1}{1 + \frac{x}{n}} \cdot \frac{-x}{n^2} }{\displaystyle \frac{-1}{n^2}}$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \lim_{n \to \infty} \displaystyle \frac{x}{1 + \frac{x}{n}}$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = \displaystyle \frac{x}{1 + 0}$

$\ln \left[ \displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \right] = x$

Applying the exponential function to both sides, we conclude that

$\displaystyle \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n= e^x$

In an undergraduate probability class, the problem can be viewed as a special case of a Poisson distribution approximating a binomial distribution if there’s a large number of trials and a small probability of success.

The above calculation also justifies (in Algebra II and Precalculus) how the formula for continuous compound interest $A = Pe^{rt}$ can be derived from the formula for discrete compound interest $A = P \displaystyle \left( 1 + \frac{r}{n} \right)^{nt}$

All this to say, Euler knew what he was doing when he decided that $e$ was so important that it deserved to be named.

Engaging students: Solving exponential equations

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Jesse Faltys. Her topic: solving exponential equations.

APPLICATIONS: What interesting (i.e., uncontrived) word problems using this topic can your students do now?

Once your students have learned how to solve exponential equations, they can solve many different kinds of applied problems like population growth, bacterial decay, and even investment earning interest rate. (Examples Found: http://www.education.com/study-help/article/pre-calculus-help-log-expo-applications/)

Examples

1. How long will it take for $1000 to grow to $1500 if it earns 8% annual interest, compounded monthly?

$A = P \left( 1 + \displaystyle \frac{r}{n} \right)^{nt}$

$A (t) = 1500$ , $P = 1000$ , $r = 0.08$ , and $n = 12$ .
We do not know $t$ .
We will solve this equation for $t$ and will round up to the nearest month.
In five years and one month, the investment will grow to about $1500.

2. A school district estimates that its student population will grow about 5% per year for the next 15 years. How long will it take the student population to grow from the current 8000 students to 12,000?

We will solve for t in the equation $12,000 = 8000 e^{0.05t}$ .

$12,000 = 8000 e^{0.05t}$

$1.5 = e^{0.05t}$

$0.05t = \ln 1.5$

$t = \displaystyle \frac{\ln 1.5}{0.05} \approx 8.1$

The population is expected to reach 12,000 in about 8 years.

3. At 2:00 a culture contained 3000 bacteria. They are growing at the rate of 150% per hour. When will there be 5400 bacteria in the culture?

A growth rate of 150% per hour means that $r = 1.5$ and that $t$ is measured in hours.

$5400 = 3000 e^{1.5t}$

$1.8 = e^{1.5t}$

$1.5t = \ln 1.8$

$t = \displaystyle \frac{\ln 1.8}{1.5} \approx 0.39$

At about 2:24 ( $0.39 \times 60 = 23.4$ minutes) there will be 5400 bacteria.

A note from me: this last example is used in doctor’s offices all over the country. If a patient complains of a sore throat, a swab is applied to the back of the throat to extract a few bacteria. Bacteria are of course very small and cannot be seen. The bacteria are then swabbed to a petri dish and then placed into an incubator, where the bacteria grow overnight. The next morning, there are so many bacteria on the petri dish that they can be plainly seen. Furthermore, the shapes and clusters that are formed are used to determine what type of bacteria are present.

CURRICULUM — How does this topic extend what your students should have learned in previous courses?

The students need to have a good understanding of the properties of exponents and logarithms to be able to solve exponential equations. By using properties of exponents, they should know that if both sides of the equations are powers of the same base then one could solve for x. As we all know, not all exponential equations can be expressed in terms of a common base. For these equations, properties of logarithms are used to derive a solution. The students should have a good understanding of the relationship between logarithms and exponents. Logs are the inverses of exponentials. This understanding will allow the student to be able to solve real applications by converting back and forth between the exponent and log form. That is why it is extremely important that a great review lesson is provided before jumping into solving exponential equations. The students will be in trouble if they have not successfully completed a lesson on these properties.

Technology – How can technology be used to effectively engage students with this topic?

1. Khan Academy provides a video titled “Word Problem Solving – Exponential Growth and Decay” which shows an example of a radioactive substance decay rate. The instructor on the video goes through how to organize the information from the world problem, evaluate in a table, and then solve an exponential equation. For our listening learners, this reiterates to the student the steps in how to solve exponential equations.

(http://www.khanacademy.org/math/trigonometry/exponential_and_logarithmic_func/exp_growth_decay/v/exponential-growth-functions)

2. Math warehouse is an amazing website that allows the students to interact by providing probing questions to make sure they are on the right train of thought.

For example, the question is $9^x = 27^2$ and the student must solve for $x$ . The first “hint” the website provides is “look at the bases. Rewrite them as a common base” and then the website shows them the work. The student will continue hitting the “next” button until all steps are complete. This is allowing the visual learners to see how to write out each step to successfully complete the problem.

(http://www.mathwarehouse.com/algebra/exponents/solve-exponential-equations-how-to.php)