In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.
Today’s quip is one that I’ll use surprisingly often:
If you ever meet a mathematician at a bar, ask him or her, “What is your favorite application of the Cauchy-Schwartz inequality?”
The point is that the Cauchy-Schwartz inequality arises surprisingly often in the undergraduate mathematics curriculum, and so I make a point to highlight it when I use it. For example, off the top of my head:
1. In trigonometry, the Cauchy-Schwartz inequality states that

for all vectors 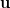 and
and 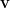 . Consequently,
. Consequently,
 ,
,
which means that the angle
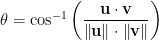
is defined. This is the measure of the angle between the two vectors 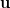 and
and 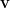 .
.
2. In probability and statistics, the standard deviation of a random variable  is defined as
is defined as
![\hbox{SD}(X) = \sqrt{E(X^2) - [E(X)]^2}](https://s0.wp.com/latex.php?latex=%5Chbox%7BSD%7D%28X%29+%3D+%5Csqrt%7BE%28X%5E2%29+-+%5BE%28X%29%5D%5E2%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
The Cauchy-Schwartz inequality assures that the quantity under the square root is nonnegative, so that the standard deviation is actually defined. Also, the Cauchy-Schwartz inequality can be used to show that  implies that
implies that  is a constant almost surely.
is a constant almost surely.
3. Also in probability and statistics, the correlation between two random variables  and
and  must satisfy
must satisfy
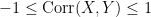 .
.
Furthermore, if 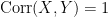 , then
, then 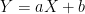 for some constants
for some constants  and
and 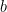 , where
, where  . On the other hand, if
. On the other hand, if 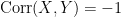 , if
, if 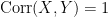 , then
, then 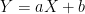 for some constants
for some constants  and
and 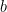 , where
, where  .
.
Since I’m a mathematician, I guess my favorite application of the Cauchy-Schwartz inequality appears in my first professional article, where the inequality was used to confirm some new bounds that I derived with my graduate adviser.

