Square roots and logarithms without a calculator (Part 2)

I’m in the middle of a series of posts concerning the elementary operation of computing a square root. This is such an elementary operation because nearly every calculator has a $\sqrt{~~}$ button, and so students today are accustomed to quickly getting an answer without giving much thought to (1) what the answer means or (2) what magic the calculator uses to find square roots.

I like to show my future secondary teachers a brief history on this topic… partially to deepen their knowledge about what they likely think is a simple concept, but also to give them a little appreciation for their elders. Indeed, when I show this method to today’s college students, they are absolutely mystified that a square root can be extracted by hand, without the aid of a calculator.

To begin, let’s again go back to a time before the advent of pocket calculators… say, ancient Rome. (I personally love using Back to the Future for the pedagogical purpose of simulating time travel, but I already used that in the previous post.)

How did previous generations figure out $\sqrt{4213}$ without a calculator? In the previous post, I introduced a trapping method that directly used the definition of $\sqrt{~~}$ for obtaining one digit at a time. Here’s a second trapping method that’s significantly more efficient. As we’ll see, this second method works because of base-10 arithmetic and a very clever use of Algebra I. My understanding is that this procedure was a standard topic in the mathematical training of children as little as 50 years ago.

Personally, I was taught this method when I was maybe 10 or 11 years old by my math teacher; I don’t doubt that she had to learn to extract square roots by hand when she was a student. Of course, this trapping method fell out of pedagogical favor with the advent of cheap pocket calculators.

I’ll illustrate this method again with $\sqrt{4213}$ . After illustrating the method, I’ll discuss how it works using Algebra I.

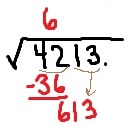
1. To begin, we start from the decimal point and group digits in block of two. (If the number had been $413$ , then the $4$ would have been in a group by itself.) I start with the $42$ . What perfect square is closest to $42$ without going over? Clearly, the answer is $6$ . So, mimicking the algorithm for long division:

We’ll place a $6$ over the $42$ , signifying that the answer is in the $60$ s.
We’ll subtract $36$ from $42$ , for an answer of $6$ .

2. On the next step, we’ll do a couple of things that are different from ordinary long division:

We’ll bring down the next two digits. So we’ll work with $613$ .
We’ll double the number currently on top and place the result to the side. In our case $6 \times 2 = 12$.
We’ll place a small ___ after the $12$ and under the $12$ .
The basic question is: I need $120$ –something times the same something to be as close to $613$ as possible without going over. I like calling this The Price Is Right problem, since so many games on that game show involve guessing a price without going over the actual price. For example…

$121 \times 1 = 121$ : too small

$122 \times 2 = 244$ : too small

$123 \times 3 = 369$ : too small

$124 \times 4 = 496$ : too small

$125 \times 5 = 625$ : too big

Based on the above work, the next digit is $4$ . We place the $4$ over the next block of digits and subtract $124 \times 4 = 496$ from $613$ . So we will work with $613-496 = 117$ on the next step.

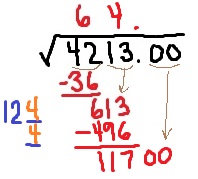3. On the next step, we’ll do a couple of things that are different from ordinary long division:

We’ll bring down the next two digits. On this step, the next two digits are the first two zeroes after the decimal point. So we’ll work with $11,700$ .
We’ll double the number currently on top and place the result to the side. In our case $64 \times 2 = 128$.
We’ll place a small ___ after the $128$ and under the $128$ .
The basic question is: I need $1280$ –something times the same something to be as close to $11,700$ as possible without going over. For example…

$1281 \times 1 = 1281$ : too small

$1282 \times 2 = 2564$ : too small

$1283 \times 3 = 3849$ : too small

$1284 \times 4 = 5136$ : too small

$1285 \times 5 = 6425$ : too small

$1286 \times 6 = 7716$ : too small

$1287 \times 7 = 9009$ : too small

$1288 \times 8 = 10,304$ : too small

$1289 \times 9 = 11,601$ : still too small

Based on the above work, the next digit is $9$ . We place the $9$ over the next block of digits and subtract $1289 \times 9 = 11,601$ from $11,700$ . So we will work with $11,700-11,601 = 99$ on the next step.

Then, to quote The King and I, et cetera, et cetera, et cetera. Each step extracts an extra digit of the square root. With a little practice, one gets better at guessing the correct value of $x$ .

A personal story: when I was a teenager and too cheap to buy a magazine, I would extract square roots to kill time while waiting in the airport for a flight to start boarding. My parents hated missing flights, so I was always at the gate with plenty of time to spare… and I could extract about 20 digits of $\sqrt{2}$ while waiting for the boarding announcement.

So why does this algorithm work? I offer a thought bubble if you’d like to think about before I give the answer.

P.S. In case anyone complains, the people of ancient Rome could not have performed this algorithm since they used Roman numerals and not a base 10 decimal system.

To see why this works, let’s consider the first two steps of finding $\sqrt{4213}$ . Clearly, the answer lies between $60$ and $70$ somewhere (that was Step 1). So the basic problem is to solve for $x$ if

$(60+x)^2 = 4213$ ,

where $x$ is the excess amount over $60$ . Squaring, we obtain

$3600 + 120x + x^2 = 4213$ ,

$120x + x^2 = 613$ ,

$(120+x)x = 613$

Notice that the right-hand side is $4213-3600$ , which was obtained at the start of Step 2. The left-hand side has the form $120$ –something times the same something, which was the key part of completing Step 2. So the value of $x$ that gets $(120+x)x$ as close to $613$ as possible (without going over) will be the next digit in the decimal representation of $\sqrt{4213}$ .

The logic for the remaining digits is similar.

I should mention that third roots, fourth roots, etc. can (in principle) be found using algebra to find excess amounts. However, it’s quite a bit more work for these higher roots. For example, to find the cube root of $4213$ , we immediately see that $10^3 = 1000 < 4213 < 8000 = 20^3$ , so that the answer lies between $10$ and $20$ . To find the excess amount over 10, we need to solve

$(10+x)^3 = 4213$ ,

which reduces to

$(300 + 30x + x^2)x = 3213$ .

So we then try out values of $x$ so that the left-hand side gets as close to $3213$ as possible without going over.

In closing, in honor of this method, here’s a great compilation of clips from The Price Is Right when the contestant guessed a price that was quite close to the actual price without going over.

http://www.youtube.com/watch?v=IHWOMyYT0jM

Square roots and logarithms without a calculator (Part 1)

This post begins a series of posts concerning the elementary operation of computing a square root. This is such an elementary operation because nearly every calculator has a $\sqrt{~~}$ button, and so students today are accustomed to quickly getting an answer without giving much thought to (1) what the answer means or (2) what magic the calculator uses to find square roots.

To begin, let’s go back to a time before the advent of pocket calculators… say, 1955. (When actually teaching this in class, I find the movie clip to be a great and brief way to get students into the mindset of going back in time.)

How did people in 1955 figure out $\sqrt{4213}$ ? After all, plenty of marvelous feats of engineering were made before the advent of calculators. So was this computed back then?

One rudimentary method is simply by trapping the solution. In other words, let’s try guessing the answer to $x^2 = 4213$ and see if we get it right.

1. First, the tens digit.

$60^2 = 3600$ . Too small.
$70^2 = 4900$ . Too big.
Since $3600 < 4213 < 4900$ , the answer has to be somewhere between $60$ and $70$ .

2. Next, the ones digit. Since $4213$ is about halfway between $3600$ and $4900$ , let’s start by guessing $65$ .

$65^2 = 4225$ . Too big, but not much too big. So let’s try $64$ next, as opposed to $62$ or $63$ .
$64^2 = 4096$ . Too small.
So the answer has to be somewhere between $64$ and $65$ .

3. Next, the tenth digit. Since $4213$ is so close to $4225$ , let’s start closer to $65$ than to $64$ .

$64.8^2 = 4199.04$
$64.9^2 = 4212.01$
We already know that $65.0^2 = 4225$
So the answer has to be somewhere between $64.9$ and $65$ .

And we keep repeating this procedure, obtaining one digit at a time. (My next guess, for the hundredths digit, would be $64.91$ or $64.92$ .) Back in 1955, all of the above squaring was done by hand, without a calculator. With enough patience, $\sqrt{4213}$ can be obtained to as many digits as required.

I distinctly remember using this procedure, just for the fun of it, when I was 7 or 8 years old (with the help of calculator, however). This exercise was far more cumbersome that simply hitting the $\sqrt{~~}$ button, but it really developed my number sense as a young child, not to mention internalizing the true meaning of what a square root actually was. Little insights like “let’s start closer to $65$ than to $64$ just don’t come naturally without this kind of trial-and-error practice.

For what it’s worth, the above procedure is the essence of the binary search algorithm (from computer science) or the method of successive bisections (from numerical analysis), with a little human intuition thrown in for good measure.

Binary sudoku

After a week of posts on Taylor series, I thought something on the lighter side would be appropriate.

Source: http://www.xkcd.com/74/

Fourier transform

Source: http://www.smbc-comics.com/index.php?db=comics&id=2874#comic

More on divisibility

Based on my students’ reactions, I gave my best math joke in years as I went over the proofs for checking that an integer was a multiple of 3 or a multiple of 9. I started by proving a lemma that 9 is always a factor of $10^k - 1$ . I asked my students how I’d write out $10^k - 1$ , and they correctly answered $99{\dots}9$ , a numeral with $k$ consecutive $9$ s. So I said, “Who let the dogs out? Me. See: $k$ nines.”

Some of my students laughed so hard that they cried.

There are actually at least three ways of proving this lemma. I love lemmas like these, as they offer a way of, in the words of my former professor Arnold Ross, to think deeply about simple things.

(1) By subtracting, $10^k - 1 = 99{\dots}9 = 9 \times 11{\dots}1$ , which is clearly a multiple of 9.

(2) We can use the rule

$a^k - b^k = (a-b) \left(a^{k-1} + a^{k-2} b + \dots + a b^{k-2} + b^{k-1} \right)$

The conclusion follows by letting $a = 10$ and $b =1$ .

From my experience, my senior math majors all learned the rule for factoring the difference of two squares, but very few learned the rule for factoring the difference of two cubes, while almost none of them learned the general factorization rule above. As always, it’s not my students’ fault that they weren’t taught these things when they were younger.

I also supplement this proof with a challenge to connect Proof #2 with Proof #1… why does $11{\dots}1 = \left(a^{k-1} + a^{k-2} b + \dots + a b^{k-2} + b^{k-1} \right)$ ?

(3) We can use mathematical induction.

If $k = 0$ , then $10^k - 1 = 0$ , which is a multiple of 9.

We now assume that $10^k - 1$ is a multiple of 9.

To show that $10^{k+1}-1$ is a multiple of 9, we observe that

$10^{k+1}-1 = \left(10^{k+1} - 10^k \right) + \left(10^k - 1\right) = 10^k (10-1) + \left(10^k - 1\right)$ ,

and both terms on the right-hand side are multiples of 9. (I also challenge my students to connect the right-hand side with the original expression $99{\dots}9$ .)

$\hbox{QED}$

Divisibility tricks

Based on personal experience, about half of our senior math majors never saw the basic divisibility rules (like adding the digits to check if a number is a multiple of 3 or 9) when they were children. I guess it’s also possible that some of them just forgot the rules, but I find that hard to believe since they’re so simple and math majors are likely to remember these kinds of tricks from grade school. Some of my math majors actually got visibly upset when I taught these rules in my Math 4050 class; they had been part of gifted and talented programs as children and would have really enjoyed learning these tricks when they were younger.

Of course, it’s not my students’ fault that they weren’t taught these tricks, and a major purpose of Math 4050 is addressing deficiencies in my students’ backgrounds so that they will be better prepared to become secondary math teachers in the future.

My guess that the divisibility rules aren’t widely taught any more because of the rise of calculators. When pre-algebra students are taught to factor large integers, it’s no longer necessary for them to pre-check if 3 is a factor to avoid unnecessary long division since the calculator makes it easy to do the division directly. Still, I think that grade-school students are missing out if they never learn these simple mathematical tricks… if for no other reason than to use these tricks to make factoring less dull and more engaging.

A mathematical magic trick

In case anyone’s wondering, here’s a magic trick that I did my class for future secondary math teachers while dressed as Carnac the Magnificent. I asked my students to pull out a piece of paper, a pen or pencil, and (if they wished) a calculator. Here were the instructions I gave them:

Write down just about any number you want. Just make sure that the same digit repeated (not something like 88,888). You may want to choose something that can be typed into a calculator.
Scramble the digits of your number, and write down the new number. Just be sure that any repeated digits appear the same number of times. (For example, if your first number was 1,232, your second number could be 2,231 or 1,322.)
Subtract the smaller of the two numbers from the bigger, and write down the difference. Use a calculator if you wish.
Pick any nonzero digit in the difference, and scratch it out.
Add up the remaining digits (that weren’t scratched out).

I asked my students one at a time what they got after Step 5, and I responded, as the magician, with the number that they had scratched out. One student said 34, and I answered 2. Another said 24, and I answered 3. After doing this a couple more times, one student simply stated, “My mind is blown.”

This is actually a simple trick to perform, and the mathematics behind the trick is fairly straightforward to understand. Based on personal experience, this is a great trick to show children as young as 2nd or 3rd grade who have figured out multiple-digit subtraction and single-digit multiplication.

I offer the following thought bubble if you’d like to think about it before looking ahead to find the secret to this magic trick.

What the magician does: the magician finds the next multiple of 9 greater than the volunteer’s number, and answers with the difference. For example, if the volunteer answers 25, the magician figures out that the next multiple of 9 after 25 is 27. So 27-25 = 2 was the digit that was scratched out.

This trick works because of two important mathematical facts.

(1) The difference $D$ between the original number and the scrambled number is always a multiple of 9. For example, suppose the volunteer chooses 3417, and suppose the scrambled number is 7431. Then the difference is

$7431 - 3417 = (7000 + 400 + 30 + 1) - (3000 + 400 + 10 + 7)$

$= (7000 - 7) + (400 - 400) + (30 - 3000) + (1 - 10)$

$= 7 \times (1000-1) + 4 \times (100-100) + 3 \times (10-1000) + 1 \times (1-10)$

$= 7 \times (999) + 1 \times (0) + 4 \times (-990) + 3 \times (-9)$

Each of the numbers in parentheses is a multiple of 9, and so the difference $D$ must also be a multiple of 9.

A more algebraic proof of (1) is set apart in the block quote below; feel free to skip it if the above numerical example is convincing enough.

More formally, suppose that the original number is $a_n a_{n-1} \dots a_1a_0$ in base-10 notation, and suppose the scrambled number is $a_{\sigma(n)} a_{\sigma(n-1)} \dots a_{\sigma(1)} a_{\sigma(0)}$ , where $\sigma$ is a permutation of the numbers $\{0, 1, \dots, n\}$ . Without loss of generality, suppose that the original number is larger. Then the difference $D$ is equal to

$D = a_n a_{n-1} \dots a_1a_0 - a_{\sigma(n)} a_{\sigma(n-1)} \dots a_{\sigma(1)} a_{\sigma(0)}$

$D = \displaystyle \sum_{i=0}^n a_i 10^i - \sum_{i=0}^n a_{\sigma(i)} 10^i$

$D = \displaystyle \sum_{i=0}^n a_{\sigma(i)} 10^{\sigma(i)} - \sum_{i=0}^n a_{\sigma(i)} 10^i$

$D = \displaystyle \sum_{i=0}^n a_{\sigma(i)} \left(10^{\sigma(i)} - 10^i \right)$

The transition from the second to the third line work because the terms of the first sum are merely rearranged by the permutation $\sigma$ .

To show that $D$ is a multiple of 9, it suffices to show that each term $10^{\sigma(i)} - 10^i$ is a multiple of 9.

If $\sigma(i) > i$ , then $10^{\sigma(i)} - 10^i = 10^i \left( 10^{\sigma(i) - i} - 1 \right)$ , and the term in parentheses is guaranteed to be a multiple of 9.

If $\sigma(i) < i$ , then $10^{\sigma(i)} - 10^i = 10^{\sigma(i)} \left( 1-10^{i-\sigma(i)} \right) = -10^{\sigma(i)} \left( 10^{i-\sigma(i)} - 1 \right)$ , and the term in parentheses is guaranteed to be a (negative) multiple of 9.

If $\sigma(i) = i$ , then $10^{\sigma(i)} - 10^i = 0$ , a multiple of 9.

$\hbox{QED}$

Because the difference $D$ is a multiple of 9, we use the important fact (2) that a number is a multiple of 9 exactly when the sum of its digits is a multiple of 9. Therefore, when the volunteer offers the sum of all but one of the digits of $D$ , the missing digit is found by determining the nonzero number that has to be added to get the next multiple of 9. (Notice that the trick specifies that the volunteer scratch out a nonzero digit. Otherwise, there would be an ambiguity if the volunteer answered with a multiple of 9; the missing digit could be either 0 or 9.)

As I mentioned earlier, I showed this trick (and the proof of why it works) to a class of senior math majors who are about to become secondary math teachers. I think it’s a terrific and engaging way of deepening their content knowledge (in this case, base-10 arithmetic and the rule of checking that a number is a multiple of 9.)

As thanks for reading this far, here’s a photo of me dressed as Carnac as I performed the magic trick. Sadly, most of the senior math majors of 2013 were in diapers when Johnny Carson signed off the Tonight Show in 1992, so they didn’t immediately get the cultural reference.

Good use of hexadecimal

This morning, I had the pleasant thought that I still am only 29 years old… as long as I use hexadecimal.

Binary magic trick

I found this magic trick in a set of Christmas crackers a couple years ago which is completely based on binary arithmetic. The link above does a good job of explaining why the trick works — and how a new trick can be generated using base-3 arithmetic.