Different definitions of e (Part 3): Discrete compound interest

In this series of posts, I consider how two different definitions of the number $e$ are related to each other. The number $e$ is usually introduced at two different places in the mathematics curriculum:

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
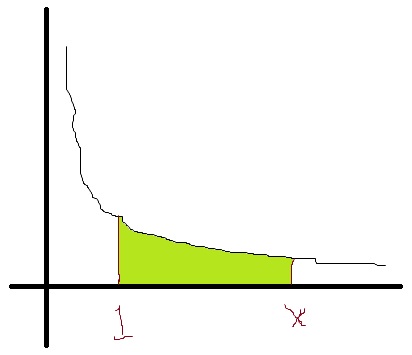
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

These two definitions appear to be very, very different. One deals with making money. The other deals with the area under a hyperbola. Amazingly, these two definitions are related to each other. In this series of posts, I’ll discuss the connection between the two.

I should say at the outset that the second definition is usually considered the true definition of $e$ . However, compound interest usually appears earlier in the mathematics curriculum than definite integrals, and so an informal definition of $e$ is given at that stage of the curriculum.

At this point in the exposition, I have justified the formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ for computing the value of an investment when interest is compounded $n$ times a year. In tomorrow’s post, I’ll discuss how the above formula naturally leads to the formula $A = P e^{rt}$ when interest is continuously compounded.

The bridge between these two formulas is considering increasing values of $n$ . So far in the presentation, we have considered an investment of $1000 making 4% interest for 2 years. In the first post of this series, we made the following computations:

1. If interest is compounded annually ( $n = 1$ ), then $A = \$1000(1.04)^2 = \$1081.60$ .

2. If interest i compounded semiannually ( $n = 2$ ), then $A = \$1000(1.02)^4 \approx \$1082.43$ .

3. If interest is compounded quarterly ( $n = 4$ ), then $A = \$1000(1.01)^8 \approx \$1082.86$ .

So I ask my class, “What happens to the final amount as interest is compounded more frequently?” They easily observe that the final amount increases somewhat. A natural question, then, is to find how much it can increase. So let’s make the compounding more frequent and let’s see what happens.

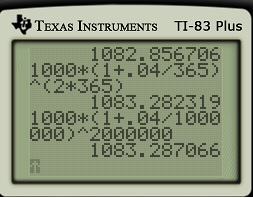
4. Daily: ( $n = 365$ ). Then $A = \$1000 \displaystyle \left( 1 + \frac{0.04}{365} \right)^{730} \approx \$1083.28$ .

5. About twice a minute ( $n = 1,000,000$ ): Then $A = \$1000 \displaystyle \left( 1 + \frac{0.04}{1,000,000} \right)^{2,000,000} \approx \$1083.29$ .

Of course, I perform all of these calculations in real time on a calculator so that students can follow along:

Students quickly observe that the final amount continues to increase as $n$ increases. However, the final amount appears to be leveling off… we can’t make the final amount arbitrarily large just by compounding the interest more frequently.

This provides a natural bridge to continuous compound interest, the topic of tomorrow’s post.

I’ll also note parenthetically that this is why financial institutions are required to disclose the annual percentage rate of a loan (among other things). Otherwise, banks could get away with declaring “Only 2% interest monthly!!” That sounds like 24% annual interest. However, $(1.02)^{12} \approx 1.26824$ , and so the annual percentage rate would really be 26.824%.

Different definitions of e (Part 2): Discrete compound interest

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

In yesterday’s post, I used a numerical example to justify the compound interest formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ when interest is compounded $n$ times a year. In a couple of days, I’ll discuss how the above formula naturally leads to the formula $A = P e^{rt}$ when interest is continuously compounded. Today, I’d like to give some pedagogical thoughts about both formulas.

The mathematics in yesterday’s post was pretty straightforward: apply the simple interest formula $I = P r t$ a few times and see if a pattern can be developed. However, my observation is that college students have no memory of being taught how the compound interest formula $A = P \displaystyle \left( 1 + \frac{r}{n} \right)^{nt}$ can be seen as a natural consequence of the simple interest formula. In other words, they’d just use the compound interest formula without having any conceptual understanding of where the formula came from.

For my math majors who aspire to become secondary teachers in the future, I’ll make my observation that there’s absolutely no reason why students couldn’t discover this formula on their own similar to the outline above. Doubtlessly, it would take more time that I use in my college class… I can usually cover the points in yesterday’s post in about 10 minutes or less, even allowing for students to pause and interject the next step of the calculation. So while the pace would be slower for a class of high school students, the mathematical ideas are simple enough to be understood by high school students.

Different definitions of e (Part 1): Discrete compound interest

In the previous series of posts, I consider how two different definitions of a logarithmic function are actually related to each other. In this series of posts, I consider how two different definitions of the number $e$ are related to each other.

The number $e$ is usually introduced at two different places in the mathematics curriculum:

Algebra II/Precalculus: If $P$ dollars are invested at interest rate $r$ for $t$ years with continuous compound interest, then the amount of money after $t$ years is $A = Pe^{rt}$ .
Calculus: The number $e$ is defined to be the number so that the area under the curve $y = 1/x$ from $x = 1$ to $x = e$ is equal to $1$ , so that

$\displaystyle \int_1^e \frac{dx}{x} = 1$ .

I begin this series of posts with a justification for the compound interest formula $A = \displaystyle P \left(1 + \frac{r}{n} \right)^{nt}$ when interest is compounded $n$ times a year. My experience is that most math majors are familiar with this formula from their high school experience but have absolutely no idea about why it is true, and so the presentation below fills in a major hole in their preparation to become secondary teachers themselves.

In the near future, I’ll discuss how the above formula naturally leads to the formula $A = P e^{rt}$ when interest is continuously compounded.

I start with a sequence of numerical examples.

A. Suppose that you invest $1,000 at 4% interest for 2 years. (At the time of this writing, a fixed interest rate of 4% is almost mythological, but let’s leave that aside for the sake of the problem.) How much money do you have if the money is compounded annually? Here are the brute force steps. (To make the presentation less dry, I make sure that my students are volunteering each answer before proceeding to the next step.)

Amount of interest earned in Year 1 = $\$1000(0.04) = \$40$ .
Total amount of money after Year 1 = $\$1000 + \$40 = \$1040$ .
Amount of interest earned in Year 2 = $\$1040(0.04) = \$41.60$ .
Total amount of money earned in Year 2 = $\$1040 + \$41.60 = \$1081.60$ .

B. Let’s repeat the above problem, except this time the 4% interest is compounded twice a year. In other words, 2% interest is applied every six months.

Amount of interest earned in first six months = $\$1000(0.02) = \$20$ .
Total amount of money after first six months = $\$1000 + \$20 = \$1020$ .
Amount of interest earned in second six months = $\$1020(0.02) = \$20.40$ .
Total amount of money earned after second six months = $\$1020 + \$20.40 = \$1040.40$ .

At this point, I’ll make a big production about how much work this is, and we’re only halfway done with this calculation! So, I’ll rhetorically ask my class, is there an easier way to do this? Let’s take a look back at the first calculation, adding some observations.

Amount of interest earned in Year 1 = $\$1000(0.04)$ .
Total amount of money after Year 1 = $\$1000 + \$1000(0.04) = \$1000(1 + 0.04) = \$1040$ .
Amount of interest earned in Year 2 = $\$1040(0.04)$ .
Total amount of money earned in Year 2 = $\$1040 + \$1040(0.04) = \$1040(1 + 0.04) = \$1000 (1+0.04)(1+0.04)$

$= \$1000(1+0.04)^2$ .

Then I’ll check with a calculator to confirm that $\$1000(1+0.04)^2$ is indeed equal to $\$1081.60$ .

Let’s now return to the problem when the 4% interest is compounded twice a year. We’re only halfway through the calculation, but let’s recapitulate what we’ve done so far. Since this is very similar to the above work, students usually can produce the logic very quickly.

Amount of interest earned in first six months = $\$1000(0.02)$ .
Total amount of money after first six months = $\$1000 + \$1000(0.02) = \$1000(1+0.02) = \$1020$ .
Amount of interest earned in second six months = $\$1020(0.02)$ .
Total amount of money earned after second six months = $\$1020 + \$1020(0.02) = \$1020(1 + 0.02) = \$1000(1+0.02)(1+0.02)$ .

$= \$1000(1+0.02)^2$ .

At this point, I’ll ask my class what they think how much money will accumulate after two years. Invariably, they guess the correct answer of $latex $1000(1+0.02)^4$. If my class seems to get it, I usually will just accept this as the correct answer without explicitly running through steps 5 through 8 to get to the end of the fourth six weeks.

C. What is the money makes 4% interest compounded four times a year for 2 years? By this point, my students can usually guess the answer: $A = 1000(1.01)^8$ . The $0.01$ comes from dividing the 4% into four parts. The 8 comes from the number of compounding periods over 2 years.

D. By this point, we have pretty much arrived at the compound interest formula: $A = P \displaystyle \left(1 + \frac{r}{n} \right)^{nt}$ . The above argument justifies the formula; the actual proof of the formula is very similar to the above numerical examples, and so I don’t use class time to formally prove it.

Tomorrow, I’ll give some pedagogical thoughts about these computations.

Different definitions of logarithm (Part 8)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $a > 0$ and $a \ne 1$ , then $f(x) = \log_a x$ is the inverse function of $g(x) = a^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

In the previous posts of this series, we established the connection between these two apparently different ways of defining a logarithm.

In this post, I describe some natural consequences of Definition 2 as it relates to calculus involving logarithmic and exponential functions. None of the results that follow are new to the senior math majors taking my capstone course. However, they almost unanimously tell me that they never learned why these rules worked when they were taking the calculus sequence several semesters ago… instead, they were given these rules to just memorize without worrying about where they came from. (I don’t doubt that some of them were taught the logical development that’s shown below, but perhaps they forgot about it since they were never held responsible for this logical development on homework or exams when they were freshmen or sophomores.)

A pedagogical note: because none of these theorems should be a surprise to students, I’ll write the left-hand sides and the equal sign on the board and then leave the right-hand side blank. After my students tell me what the punch line of the theorem should be, then I’ll write the complete statement of the theorem on the board before proceeding to the proof. If my students can’t remember the punch-line (which has happened for Theorem 2 below), I’ll just start the proof until we reach the conclusion and then fill in the blank right-hand side of the theorem’s statement later.

Theorem 1. $\displaystyle \frac{d}{dx} (\ln x) = \displaystyle \frac{1}{x}$

Proof. This is a consequence of the Fundamental Theorem of Calculus. Loosely stated, the derivative of an integral is the original function.

Theorem 2. $\displaystyle \frac{d}{dx} (\log_a x) = \displaystyle \frac{1}{x \ln a}$

Proof. This is a consequence of the change-of-base formula:

$\log_a x = \displaystyle \frac{\log_e x}{\log_e a} = \displaystyle \frac{\ln x}{\ln a}$

$\frac{d}{dx} \left( \log_a x \right) = \displaystyle \frac{d}{dx} \left( \frac{\ln x}{\ln a} \right)$

Since $\ln a$ is just a constant, we conclude

$\frac{d}{dx} \left( \log_a x \right) = \displaystyle \frac{1}{\ln a} \cdot \frac{d}{dx} ( \ln x ) = \displaystyle \frac{1}{\ln a} \cdot \frac{1}{x}$

Theorem 3. $\displaystyle \frac{d}{dx} \left( a^x \right) = a^x \ln a$

Proof. This proof uses a standard trick. Suppose that

$y = a^x$

so that

$\log_a y = x$

We need to compute the derivative $\displaystyle \frac{dy}{dx}$ . To this end, let’s apply implicit differentiation to this last equation:

$\displaystyle \frac{1}{y \ln a} \cdot \frac{dy}{dx} = 1$

$\displaystyle \frac{dy}{dx} = y \ln a$

$\displaystyle \frac{d}{dx} \left( a^x \right) = a^x \ln a$

Technical Note: The above proof assumes that the derivative $\displaystyle \frac{dy}{dx}$ exists in the first place, and so, technically, implicit differentiation is inappropriate (even if it does produce the correct answer). However, the existence proof is quite difficult, requiring an advanced version of the Mean Value Theorem. So, for pedagogical reasons, I have absolutely no qualms about showing the above proof to students in a class that does not require second-semester real analysis as a prerequisite.

Pedagogical Note: After presenting this proof to my students, students are usually emotionally stunned. They usually tell me that they never saw how the derivative of an inverse function could be computed back when they were in the calculus sequence… it was just another formula that they had to memorize. So (time permitting), to let this idea sink in a little further, I’ll go off on a tangent (pun intended)…

…to find the derivative of an inverse trigonometric function:

$y = \sin^{-1} x$

$\sin y = x$

$\cos y \cdot \displaystyle \frac{dy}{dx} = 1$

$\displaystyle \frac{dy}{dx} = \frac{1}{\cos y}$

$\displaystyle \frac{dy}{dx} = \frac{1}{\sqrt{1 - \sin^2 y}}$

$\displaystyle \frac{dy}{dx} = \frac{1}{\sqrt{1-x^2}}$

I’ll then invite students to figure out the derivatives of $y = \cos^{-1} x$ and $y = \tan^{-1} x$ on their own after class.

Theorem 4. $\displaystyle \frac{d}{dx} \left( e^x \right) = e^x$

Proof. Let $a = e$ in Theorem 3. Alternatively, repeat the above argument for the inverse functions $e^x$ and $\ln x$ .

Different definitions of logarithm (Part 7)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $a > 0$ and $a \ne 1$ , then $f(x) = \log_a x$ is the inverse function of $g(x) = a^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

The connection between these two apparently different ideas begins with the following theorem, which was proven in the few previous posts.

Theorem. Let $a \in \mathbb{R}^+ \setminus \{1\}$ . Suppose that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ has the following four properties:

$f(1) = 0$

$f(a) = 1$

$f(xy) = f(x) + f(y)$ for all $x, y \in \mathbb{R}^+$

$f$ is continuous

Then $f(x) = \log_a x$ for all $x \in \mathbb{R}^+$ .

At this point, we have provided enough groundwork to make the connection between these two different ways of viewing a logarithm.

Let’s define the function (for $x > 0$ )

$A(x) = \displaystyle \int_1^x \frac{1}{t} dt$ .

I’ll illustrate this with the appropriate area under the hyperbola $y = \frac{1}{x}$ . (Please forgive the crudeness of this drawing; I’m only using Microsoft Paint.)

So if $x$ is the right-hand limit, then $A(x)$ is just the shaded area under the curve.

Often, someone will interject, “Hey, I know how to do that… it’s just the natural logarithm of $x$ .” To which I will respond, “Yes, that’s true. But why is it the natural logarithm of $x$ ?” I have yet to encounter a student who can immediately answer this question (which, of course, is the whole point of me presenting this in class). In other words, I want my students to realize that, many semesters ago, they pretty much accepted on faith that the above integral is equal to $\ln x$ , but they were never told the reason why. And now — several semesters after completing the calculus sequence — we’re finally going over the reason why.

To start, I’ll say, “OK, $A$ is defined as an integral. That means that it must have…” Someone will usually volunteer, “A derivative.” I’ll respond, “That’s right. The Fundamental Theorem of Calculus says that this function is differentiable. So, if something is differentiable, then it also must be…” Someone will usually volunteer, “Continuous.” My response: “That’s right. So $A$ must be continuous. So that’s Property 4: this function is continuous.” I’ll continue: “Let’s see if we can get the other properties.”

I’ll next move to Property 1, as it’s the next easiest. I’ll ask the class, “Can you prove to me that $A(1) = 0$ ?” After a moment of thought, someone will notice that

$A(1) = \displaystyle \int_1^1 \frac{1}{t} dt$ .

must be equal to $0$ since the left and right endpoints of the integral are the same.

Then I’ll skip over to Property 3, which requires a little more thought. To begin, we can write

$A(xy) = \displaystyle \int_1^{xy} \frac{1}{t} dt = \displaystyle \int_1^{x} \frac{1}{t} dt + \int_x^{xy} \frac{1}{t} dt$ .

Before proceeding, I’ll ask my class why the above line has to be true. After a couple moments, someone will volunteer something like “The area from $1$ to $x$ plus the area from $x$ to $xy$ has to be equal to the area from $1$ to $xy$ .”

I’ll then say something like, “We can simplify one of the integrals on the right-hand side right away. Which one?” Students quickly see that the first integral on the right, $\displaystyle \int_1^{x} \frac{1}{t} dt$ , is of course equal to $A(x)$ . So then I’ll ask, “So what do I want the last integral to be equal to?” Students look back at Property 3 and answer, “That should be $A(y)$ .

So, if we can show the final integral is equal to $A(y)$ , we have established Property 3. To this end, I will perform a somewhat unusual looking $u-$ substitution:

$t = ux$

In this formula, I encourage my students to think of $t$ as the old variable of integration, $u$ as the new variable of integration, and $x$ as an unknown number that is constant. So I’ll say parenthetically, “If $t = 5u$ , how do we find $dt$ ?” Students of course answer, “ $dt$ must be $5 du$ .” So I’ll follow up: “If $t = xu$ , how do we find $dt$ ?” Students get the idea:

$t = x \, du$

So to complete the $u-$ substitution, we must adjust the limits of integration. For the lower limit,

$t = x \Longrightarrow u = \displaystyle \frac{x}{x} = 1$

For the upper limit,

$t = xy \Longrightarrow u = \displaystyle \frac{xy}{x} = y$

So we can now complete the $u-$ substitution of the second integral:

$A(xy) = \displaystyle \int_1^{xy} \frac{1}{t} dt = \displaystyle \int_1^{x} \frac{1}{t} dt + \int_x^{xy} \frac{1}{t} dt$ .

$A(xy) = \displaystyle \int_1^{x} \frac{1}{t} dt + \int_1^{y} \frac{1}{xu} x \, du$ .

$A(xy) = \displaystyle \int_1^{x} \frac{1}{t} dt + \int_1^{y} \frac{1}{u} \, du$ .

Students recognize that, except for the variable of integration, the last integral is just $A(y)$ , which leads to the punch line

$A(xy) = A(x) + A(y)$

In other words, we have established that the function $A$ satisfies Property 3.

So the only property left is Property 2. To that end, let’s define the number $e$ so that the area in green above is equal to 1. There’s no other way to describe this number…. we just increase $x$ far enough along the $x-$ axis until the area under the hyperbola is equal to 1. Wherever this happens, that’s the number that we’ll call $e$ . So, by definition, $A(e) = 1$ .

Therefore, by the above theorem, we conclude that $A(x) = \log_e x$ , written more simply as $\ln x$ .

To summarize: using the above theorem, we are able to establish that the integral $\displaystyle \int_1^x \frac{1}{t} dt$ has all of the properties of a logarithm and therefore must be a logarithmic function. The only catch is that we had to define $e$ to be the base of this logarithm through an unusual definition concerning the area under a hyperbola.

Of course, this is not the “standard” definition of $e$ that is usually encountered in a Precalculus class. More on these different definitions in a future series of posts.

One more pedagogical note: My experience is that I can cover the content of the first 7 posts of this series in a single 50-minute lecture and still keep my students’ attention. Naturally, I’ll recapitulate the highlights of this logical development at the start of the next lecture by way of review, as this is an awful lot to absorb at once.

Different definitions of logarithm (Part 6)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $a > 0$ and $a \ne 1$ , then $f(x) = \log_a x$ is the inverse function of $g(x) = a^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

The connection between these two apparently different ideas begins with the following theorem.

Theorem. Let $a \in \mathbb{R}^+ \setminus \{1\}$ . Suppose that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ has the following four properties:

$f(1) = 0$

$f(a) = 1$

$f(xy) = f(x) + f(y)$ for all $x, y \in \mathbb{R}^+$

$f$ is continuous

Then $f(x) = \log_a x$ for all $x \in \mathbb{R}^+$ .

Note. To prove this theorem, I will show that $f(a^x) = x$ , thus proving that $f$ is the inverse of $g(x) = a^x$ .

The proof of these theorem divides into four cases:

Positive integers: $x = m \in \mathbb{Z}^+$
Positive rational numbers: $x = \frac{m}{n}$ , where $m,n \in \mathbb{Z}^+$
Negative rational numbers: $x \in \mathbb{Q}^-$
Real (possibly irrational) numbers: $x \in \mathbb{R}$

In today’s post, I’ll complete the proof by handling Case 4.

Before starting Case 4, I like to take inventory of where we stand in the proof at this point. We have now proven the theorem for all positive rational numbers and for all negative rational numbers. There’s only one rational number left: $x = 0$ . And this single case is simply handled through Property 1:

$f(a^0) = f(1) = 0$

I also like to keep track of which hypotheses have been used so far in the proof. A quick review of Cases 1-3 will reveal that Properties 1-3 have all been used at least once, but Property 4 (the assumption that $f$ is continuous) has not be used so far. Therefore, we had better expect to use it before completing the proof.

I won’t tell the class this (for fear of discouraging them), but the proof of Case 4 is a bit more abstract than Cases 1-3. I can give a numerical example that (hopefully) will shed some insight into the actual proof. However, for Case 4, the actual proof will not be a perfect parallel of the numerical example (as in Cases 1-3).

Idea behind Case 4. Let’s pick a familiar irrational number like $\sqrt{2}$ . There is a natural way to approximate $\sqrt{2}$ by a sequence of rational numbers… namely, the sequence of numbers obtained by taking one extra digit in the decimal expansion of $\sqrt{2}$ . In other words,

$r_1 = 1$

$r_2 = 1.4$

$r_3 = 1.41$

$r_4 = 1.414$

and so on.

In this way, $\displaystyle \lim_{n \to \infty} r_n = \sqrt{2}$ .

We would hope that the sequence

$f \left( a^1 \right), f \left( a^{1.4} \right), f \left( a^{1.41} \right), f \left( a^{1.414} \right), \dots$

converges to the obvious limit of

$f \left( a^{\sqrt{2}} \right)$ .

However, this sequence is also equal to

$1, 1.4, 1.41, 1.414, \dots$

since each exponent is rational. Since a sequence has only one limit, we conclude that these two limits should be equal:

$\sqrt{2} = f \left( a^{\sqrt{2}} \right)$

So that’s the idea of the formal proof, which we now tackle. In the proof below, I’ve marked with quotations some of the more parenthetical steps so that the main argument of the proof stands out a little bit better. You’ll notice that, unlike Cases 1-3, I don’t use as much directed questioning to get students to volunteer the next step of the proof with minimal assistance from me. That’s because I haven’t figured out a good way to use inquiry to quickly get through Case 4.

Proof of Case 4. Let $\{ r_n \}$ be a sequence of rational numbers that converges to $x$ . (Parenthetically, I’ll mention that the sequence of decimal approximations would be one such sequence, just to make this mysterious $\{ r_n \}$ thing that just appeared out of the blue a little less daunting. Of course, any sequence of rational numbers that converges to $x$ will do. Therefore,

$f \left( a^x \right) = f \left( a^{\lim_{n \to \infty} r_n} \right)$

The function $g(x) = a^x$ is continuous. From the ordinary definition of continuous used in calculus, this means that

$\displaystyle \lim_{x \to c} g(x) = g(c)$ .

In other words, the function and the limit can be interchanged. (I’ll usually throw in my standard joke about functions commuting at this point in the lecture.) Stated in terms of a sequence $r_n \to x$ , this means that

$\displaystyle \lim_{n \to \infty} g(r_n) = g(x) = g \left( \lim_{n \to \infty} r_n \right)$ .

Stated another way,

$\displaystyle \lim_{n \to \infty} a^{r_n} = a^{ \lim_{n \to \infty} r_n}$ .

In light of the above work, we conclude that

$f \left( a^x \right) = f \left( a^{\lim_{n \to \infty} r_n} \right) = f \left( \displaystyle \lim_{n \to \infty} a^{r_n} \right)$

Stated simply, the function and the limit interchange.

We now perform a similar step for the function $f$ . Because $f$ is assumed to be continuous, we know that

$\displaystyle \lim_{n \to \infty} f(s_n) = f(c) = f \left( \lim_{n \to \infty} s_n \right)$

if $\{ s_n \}$ is a sequence that converges to $c$ . So, if we replace $s_n$ by $a^{r_n}$ and $c$ by $\displaystyle \lim_{n \to \infty} a^{r_n}$ , we conclude that

$\displaystyle \lim_{n \to \infty} f \left( a^{r_n} \right) = f \left( \displaystyle \lim_{n \to \infty} a^{r_n} \right)$

From the above insight, we see that we have the next step of the proof:

$f \left( a^x \right) = f \left( a^{\lim_{n \to \infty} r_n} \right)$

$= f \left( \displaystyle \lim_{n \to \infty} a^{r_n} \right)$

$= \displaystyle \lim_{n \to \infty} f \left(a^{r_n} \right)$

From now on, the concluding steps are pretty straightforward. The exponent on the last line is a rational number. Therefore, by Cases 2 and 3, we have produce the next step:

$f \left( a^x \right) = f \left( a^{\lim_{n \to \infty} r_n} \right)$

$= f \left( \displaystyle \lim_{n \to \infty} a^{r_n} \right)$

$= \displaystyle \lim_{n \to \infty} f \left(a^{r_n} \right)$

$= \displaystyle \lim_{n \to \infty} r_n$

Finally, by definition from the top of the proof, we can evaluate this limit:

$f \left( a^x \right) = f \left( a^{\lim_{n \to \infty} r_n} \right)$

$= f \left( \displaystyle \lim_{n \to \infty} a^{r_n} \right)$

$= \displaystyle \lim_{n \to \infty} f \left(a^{r_n} \right)$

$= \displaystyle \lim_{n \to \infty} r_n$

$= x$

This concludes the proof that $f \left( a^x \right) = x$ , even if $x$ is an arbitrary (possibly irrational) real number.

Different definitions of logarithm (Part 5)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $a > 0$ and $a \ne 1$ , then $f(x) = \log_a x$ is the inverse function of $g(x) = a^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

The connection between these two apparently different ideas begins with the following theorem.

Theorem. Let $a \in \mathbb{R}^+ \setminus \{1\}$ . Suppose that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ has the following four properties:

$f(1) = 0$

$f(a) = 1$

$f(xy) = f(x) + f(y)$ for all $x, y \in \mathbb{R}^+$

$f$ is continuous

Then $f(x) = \log_a x$ for all $x \in \mathbb{R}^+$ .

Note. To prove this theorem, I will show that $f(a^x) = x$ , thus proving that $f$ is the inverse of $g(x) = a^x$ .

The proof of these theorem divides into four cases:

Positive integers: $x = m \in \mathbb{Z}^+$
Positive rational numbers: $x = \frac{m}{n}$ , where $m,n \in \mathbb{Z}^+$
Negative rational numbers: $x \in \mathbb{Q}^-$
Real (possibly irrational) numbers: $x \in \mathbb{R}$

In today’s post, I’ll describe how I prompt my students to prove Case 3 during class time. Cases 4 will appear in tomorrow’s post.

Idea behind Case 3. Though not formally necessary for the proof, I’ve found it helpful to illustrate the idea of the proof with a specific example before proceeding to the general case. So — on the far end of the chalkboard, away from the space that I’ve allocated for the formal write-up of the proof — I’ll write

$f \left( a^{-2/3} \cdot a^{2/3} \right) =$

I’ll then ask, “How else can we simplify the left-hand side?” As we’ll see below, there are actually two legitimate ways of proceeding. Someone will usually suggest just simplifying the product, and so I’ll write this as the next step:

$f \left( a^{-2/3} \cdot a^{2/3} \right) = f \left( a^0 \right)$

I’ll then ask a very open-ended question, “Now what?” Usually, someone will suggest simplifying the right-hand side using Property 1:

$f \left( a^{-2/3} \cdot a^{2/3} \right) = f \left( a^0 \right) = 0$

By this point, after completing Cases 1 and 2, someone will usually suggest expanding the left-hand side:

$f \left( a^{-2/3} \right) + f \left( a^{2/3} \right) = 0$

I’ll then ask, “What can we do now?” Hopefully, someone will observe that the second term can be simplified using Case 2:

$f \left( a^{-2/3} \right) + \displaystyle \frac{2}{3} = 0$

$f \left( a^{-2/3} \right) = - \displaystyle \frac{2}{3}$

I’ll then note that we’ve finished what we set out to do: show that $f(a^x) = x$ when $x = - \frac{2}{3}$ , a negative rational number.

The natural next question is, “Can we do this for any negative rational number and not just $-\frac{2}{3}$ ?” This leads to the proof of Case 3. I’ve found that it’s helpful to walk through this proof line by line in step with the case of $x= -\frac{2}{3}$ , so that students can see how the steps of this more abstract proof correspond to the concrete example of $x = =\frac{2}{3}$ .

Proof of Case 3. Let $m, n \in \mathbb{Z}^+$ . Then

$f \left(a^{-m/n} \cdot a^{m/n} \right) = f \left(a^0 \right)$

$f \left( a^{-m/n} \right) + f \left( a^{m/n} \right) = 0$

$f \left( a^{-m/n} \right) + \displaystyle \frac{m}{n} = 0$

$f \left( a^{-m/n} \right) = - \displaystyle \frac{m}{n}$

Again, I’ve found that the special case $x = - \frac{2}{3}$ is pedagogically helpful, if not logically necessary to prove Case 3.

Different definitions of logarithm (Part 4)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $a > 0$ and $a \ne 1$ , then $f(x) = \log_a x$ is the inverse function of $g(x) = a^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

The connection between these two apparently different ideas begins with the following theorem.

Theorem. Let $a \in \mathbb{R}^+ \setminus \{1\}$ . Suppose that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ has the following four properties:

$f(1) = 0$

$f(a) = 1$

$f(xy) = f(x) + f(y)$ for all $x, y \in \mathbb{R}^+$

$f$ is continuous

Then $f(x) = \log_a x$ for all $x \in \mathbb{R}^+$ .

Note. To prove this theorem, I will show that $f(a^x) = x$ , thus proving that $f$ is the inverse of $g(x) = a^x$ .

The proof of these theorem divides into four cases:

Positive integers: $x = m \in \mathbb{Z}^+$
Positive rational numbers: $x = \frac{m}{n}$ , where $m,n \in \mathbb{Z}^+$
Negative rational numbers: $x \in \mathbb{Q}^-$
Real (possibly irrational) numbers: $x \in \mathbb{R}$

In today’s post, I’ll describe how I prompt my students to prove Case 2 during class time. Cases 3-4 will appear in the coming posts.

Idea behind Case 2. Though not formally necessary for the proof, I’ve found it helpful to illustrate the idea of the proof with a specific example before proceeding to the general case. So — on the far end of the chalkboard, away from the space that I’ve allocated for the formal write-up of the proof — I’ll write

$2 = f(a^2)$

I’ll ask, “How do we know this is true?” The immediate answer: We just did Case 1. I’ll then do something a little unusual and rewrite this equation in a more complicated way:

$2 = f(a^2) = f \left( \left[a^{2/3} \right]^3 \right)$

After double-checking that the class agrees with this step (even if I just made the right-hand more complicated instead of the usual step of simplifying the right-hand side), I’ll then ask, “OK, we have something to the third power. What can we now do to the right-hand side?” Almost immediately, someone will volunteer the correct next steps using Property 3:

$2 = f(a^2) = f \left( a^{2/3} \cdot a^{2/3} \cdot a^{2/3} \right) = f \left( a^{2/3} \right) + f \left( a^{2/3} \right) + f \left( a^{2/3} \right)$

I’ll then ask, “How can we simplify the right-hand side?” After a moment of thought, someone will volunteer the correct next step:

$2 = f(a^2) = f \left( a^{2/3} \cdot a^{2/3} \cdot a^{2/3} \right) = f \left( a^{2/3} \right) + f \left( a^{2/3} \right) + f \left( a^{2/3} \right)$

$2 = 3 f \left( a^{2/3} \right)$

I’ll then ask, “How do we isolate the $f \left( a^{2/3} \right)$ term?” The obvious correct answer:

$\displaystyle \frac{2}{3} = f(a^{2/3})$

I’ll then note that we’ve finished what we set out to do: show that $f(a^x) = x$ when $x = \frac{2}{3}$ .

The natural next question is, “Can we do this for any positive rational number and not just $\frac{2}{3}$ ?” This leads to the proof of Case 2. I’ve found that it’s helpful to walk through this proof line by line in step with the case of $x=\frac{2}{3}$ , so that students can see how the steps of this more abstract proof correspond to the concrete example of $x =\frac{2}{3}$ .

Proof of Case 2. Let $x = \displaystyle \frac{m}{n}$ where $m, n \in \mathbb{R}^+$ . Then

$m = f(a^m)$

$m = f \left( \left[ a^{m/n} \right]^n \right)$

$m = f \left( a^{m/n} \cdot a^{m/n} \cdot \dots \cdot a^{m/n} \right)$

$m = f \left( a^{m/n} \right) + f \left( a^{m/n} \right) + \dots + f \left( a^{m/n} \right)$

$m = n f \left( a^{m/n} \right)$

$\displaystyle \frac{m}{n} = f \left( a^{m/n} \right)$

Of course, the special case $x = \frac{2}{3}$ is not logically necessary to prove Case 2. Though not logically necessary, I’ve found it to be pedagogically convenient. From the school of hard knocks, I’ve found that the proof of Case 2 goes over easier with students when they see the idea of the proof presented concretely and then abstractly.

Different definitions of logarithm (Part 3)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $a > 0$ and $a \ne 1$ , then $f(x) = \log_a x$ is the inverse function of $g(x) = a^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

The connection between these two apparently different ideas begins with the following theorem.

Theorem. Let $a \in \mathbb{R}^+ \setminus \{1\}$ . Suppose that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ has the following four properties:

$f(1) = 0$

$f(a) = 1$

$f(xy) = f(x) + f(y)$ for all $x, y \in \mathbb{R}^+$

$f$ is continuous

Then $f(x) = \log_a x$ for all $x \in \mathbb{R}^+$ .

Note. To prove this theorem, I will show that $f(a^x) = x$ , thus proving that $f$ is the inverse of $g(x) = a^x$ .

The proof of these theorem divides into four cases:

Positive integers: $x = m \in \mathbb{Z}^+$
Positive rational numbers: $x = \frac{m}{n}$ , where $m,n \in \mathbb{Z}^+$
Negative rational numbers: $x \in \mathbb{Q}^-$
Real (possibly irrational) numbers: $x \in \mathbb{R}$

In today’s post, I’ll describe how I prompt my students to prove Case 1 during class time. Cases 2-4 will appear in the coming posts.

Idea behind Case 1. Though not formally necessary for the proof, I’ve found it helpful to illustrate the idea of the proof with a specific example before proceeding to the general case. So — on the far end of the chalkboard, away from the space that I’ve allocated for the formal write-up of the proof — I’ll write

$f(a^4) =$

I’ll then ask, “How else can we write $a^4$ ?” Someone will usually suggest $a \cdot a \cdot a \cdot a$ , and so I’ll write this as the next step:

$f(a^4) = f(a \cdot a \cdot a \cdot a)$

I’ll then ask, “OK, we have a product here. How can we simplify the right-hand side?” After a moment of thought, someone will volunteer that Property 3 allows the right-hand side to be split up into pieces:

$f(a^4) = f(a \cdot a \cdot a \cdot a) = f(a) + f(a) + f(a) + f(a)$

(Technically, this requires mathematical induction to generalize Property 3 from a product of two numbers to a product of arbitrarily many numbers, but I don’t think that it’s worth the time to expound on this pedantic point.) I’ll then ask, “How can we simplify this?” Almost immediately, someone will usually volunteer Property 2:

$f(a^4) = f(a \cdot a \cdot a \cdot a) = f(a) + f(a) + f(a) + f(a) = 1 + 1 + 1 + 1 = 4$

I’ll then note that we’ve finished what we set out to do: show that $f(a^x) = x$ when $x = 4$ .

The natural next question is, “Can we do this for any positive integer and not just 4?” This leads to the proof of Case 1. I’ve found that it’s helpful to walk through this proof line by line in step with the case of $x=4$ , so that students can see how the steps of this more abstract proof correspond to the concrete example of $x =4$ .

Proof of Case 1.

$f(a^m) = f(a \cdot a \cdot \dots \cdot a)$

$= f(a) + f(a) + \dots + f(a)$

$= 1 + 1 + \dots + 1$

$= m$

Of course, the special case $x = 4$ is not logically necessary to prove Case 1. That said, from the school of hard knocks, I’ve found that the proof of Case 1 goes over easier with students when they see the idea of the proof presented concretely and then abstractly.

Different definitions of logarithm (Part 2)

There are two apparently different definitions of a logarithm that appear in the secondary mathematics curriculum:

From Algebra II and Precalculus: If $b > 0$ and $b \ne 1$ , then $f(x) = \log_b x$ is the inverse function of $g(x) = b^x$ .
From Calculus: for $x > 0$ , we define $\ln x = \displaystyle \int_1^x \frac{1}{t} dt$ .

In this series of posts, we examine the interrelationship between these two different approaches to logarithms. This is a standard topic in my class for future teachers of secondary mathematics as a way of deepening their understanding of a topic that they think they know quite well.

The connection between these two apparently different ideas begins with the following theorem.

Theorem. Let $a \in \mathbb{R}^+ \setminus \{1\}$ . Suppose that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ has the following four properties:

$f(1) = 0$

$f(a) = 1$

$f(xy) = f(x) + f(y)$ for all $x, y \in \mathbb{R}^+$

$f$ is continuous

Then $f(x) = \underline{\hspace{1in}}$ for all $x \in \mathbb{R}^+$ .

When writing this on the board, I purposefully leave an underline for my students to fill in, because I want them to think. What familiar function has these four properties? I’ll usually invoke the old chidren’s joke: “If it looks like an elephant, smells like an elephant, feels like an elephant, and sounds like an elephant, then it must be an elephant.” After a moment of thought, someone will usually volunteer $f(x) = \log x$ . That’s almost correct, and so I’ll ask if Property 2 is satisfied by this function. After a couple more moments of thought, someone will volunteer the correct answer, $f(x) = \log_a x$ .

To prove this theorem, I will show that

$f(a^x) = x$ for all $x \in \mathbb{R}$ .

I’ll make the observation that the case of $latex x=0$ is Property 1, while the case of $x = 1$ is Property 2.

Then I’ll ask the class: “If I’m able to prove that $f(a^x) = x$ for all real $x$ , why does this mean that $f(x) = \log_a x$ ?” Perhaps unsurprisingly, this usually draws blank stares for a few seconds until someone realizes that this means that $f: \mathbb{R}^+ \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}^+$ defined by $g(x) = a^x$ are inverse functions. So (by definition) $f(x)$ must be equal to $\log_a x$ .

The proof of these theorem has four parts:

Positive integers: $x = m \in \mathbb{Z}^+$
Positive rational numbers: $x = \frac{m}{n}$ , where $m,n \in \mathbb{Z}^+$
Negative rational numbers: $x \in \mathbb{Q}^-$
Real (possibly irrational) numbers: $x \in \mathbb{R}$

Beginning with tomorrow’s post, I’ll discuss how I walk students through the proof in lecture.