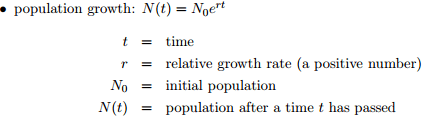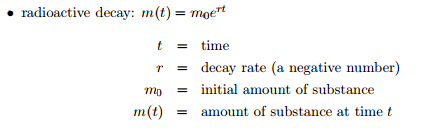Engaging students: Graphing rational functions

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Rory VerNesie. His topic, from Precalculus: graphing rational functions.

So one question may be how this topic can be used in your students future courses in math or science? The students start to learn about this concept in high school, and progressively builds on it until they are expected to know it in college. Courses that require this are: Complex Analysis, Numerical Analysis, Differential Equations, Abstract Algebra, Real Analysis and Meromorphic Functions. These classes deal with understanding what happens as we approach a limit or when the denominator approaches zero. In Abstract Algebra, they talk about a Field of Rational Expressions while Complex Analysis deals with a ratio of polynomials with complex coefficients. In Differential Equations, Rational Functions are seen in slope fields, Separable Equations, and Exact equations. Also in Real Analysis, the talk about convergence using 1/n. Also, Laplace Transforms and partial fractions in electronics and physics may need graphing along with partial fraction decomposition. All in all, graphing Rational Functions is a important part of math because they deal with division over zero or a singularity.

Next, a very important man in the history of rational functions and their graphs was Charles Hermite. This man found a way or algorithm to integrate Rational Functions, while in early 19th century Ostrowski extended this idea and algorithm to Rational Expressions. The neat thing about Hermite is that he helped extend this idea to complex numbers and developed the idea of using interpolation to find the coefficients of rational functions. Without these contributions from Hermite and Ostrowski we would not be able to graph the derivatives of rational functions or the anti derivatives of rational functions. The methods discovered by these men were profound and in some ways led to the discovery of news ideas in math such as partial decomposition and other integration techniques that help integrate Rational Functions. Without these men, Rational Functions and there uses would be known about less.

A great activity involving graphing rational functions would be to have the kids get into groups and assign the each group a certain rational function. Every group would have a team leader who would be in charge of making sure everything about the function gets done. These responsibilities would include, graphing the function, finding the zeros of the function, the asymptotes(Horizontal and Vertical), Removable Discontinuities if any, and the y intercept. The students would then present what they found and would answer any questions for the class. This activity would be a good cooperative learning exercise for students who maybe are not the best at math. This could be a major confidence booster and fun activity for the students. Also they students are learning from each other so they are engaging in discovery learning.

All in all, graphing rational functions is a major part of mathematics and all of these statements mentioned above show how important rational functions are. They deal with division by zero and limits and are a great way to engage students in the novelty of singularities. Graphing polynomials also look really neat when you graph them.

Work Cited

http://integrals.wolfram.com/about/history/

http://www.sciencedirect.com/science/article/pii/0898122176900237

tutorial.math.lamar.edu

Slideplayer.com

Engaging students: Introducing the number e

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Loc Nguyen. His topic, from Precalculus: introducing the number $e$ .

How could you as a teacher create an activity or project that involves your topic?

To be able to understand where the number e is produced in the first place, students need to understand how compound interest is calculated. Before introducing the number e, I will definitely create an activity for the students to work on so that they can eventually find the formula for compounding interest based on the patterns they produce throughout the process. The compound interest formula is F=P(1+r/n)^nt. From this formula, I will again provide students a worksheet to work on. In this worksheet, I will let P=1, r=100%, t=1, then the compound interest formula will be F=(1+1/n)ⁿ. Now students will compute the final value from yearly to secondly.

When they do all the computation, they will see all the decimal places of the final value lining up as n gets big. And finally, they will see that the final value gets to the fixed value as n goes to infinity. That number is e=2.71828162….,

How has this topic appeared in the news?

To help the students realize how important number e is, I would engage them with the real life examples or applications. There were some news that incorporated exponential curves. First, I will show the students the news about how fast deadly disease Ebola will grow through this link http://www.npr.org/sections/goatsandsoda/2014/09/18/349341606/why-the-math-of-the-ebola-epidemic-is-so-scary. The students will eventually see how exponential curve comes into play. After that I will provide them this link, http://cleantechnica.com/2014/07/22/exponential-growth-global-solar-pv-production-installation/, in this link, the article talked about the global population rate and it provided the scientific evidence that showed the data collected represent the exponential curve. Up to this point, I will show the students that the population growth model is:

Those examples above was about the growth. For the next example, I will ask the students that how the scientists figured out the age of the earth. In this link, http://earthsky.org/earth/how-old-is-the-earth, the students will learn that the scientists used Modern radiometric dating methods to calculate the age of earth. At this time, I will show them radioactive decay formula and explain to them that this formula is used to determine the lives of the substances such as rocks:

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

To introduce to the students what the number e is, I will engage them with two videos. In the first video, https://www.youtube.com/watch?v=UFgod5tmLYY, the math song “e a magic number” will engage the students why it is a magic number. While watching this clip, the students will be able to learn the history of e. Also the students will see many mathematical formulas and expressions that contain e. This will give them a heads up that they will see these in future when they take higher level math. It is also pretty humorous of how Dr. Chris Tisdell sang the song.

In the second video, https://www.youtube.com/watch?v=b-MZumdfbt8, it explained why e is everywhere. The video used probability and exponential function to illustrate the usefulness of e, and showed how e is involving in everything. It gave many examples of e such as population, finance… Also the video illustrates the characteristics of the number e and the function that has e in it. Watching these videos will enhance students’ perception and understanding on the number e, and help them to see how important this number is.

Reference

https://www.youtube.com/watch?v=b-MZumdfbt8

https://www.youtube.com/watch?v=UFgod5tmLYY

http://www.math.unt.edu/~baf0018/courses/handouts/exponentialnotes.pdf

http://cleantechnica.com/2014/07/22/exponential-growth-global-solar-pv-production-installation/

http://www.npr.org/sections/goatsandsoda/2014/09/18/349341606/why-the-math-of-the-ebola-epidemic-is-so-scary

http://earthsky.org/earth/how-old-is-the-earth

Engaging students: Graphing exponential growth and decay functions

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Irene Ogeto. Her topic, from Precalculus: graphing exponential growth and decay functions.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic? Note: It’s not enough to say “such-and-such is a great website”; you need to explain in some detail why it’s a great website.

The Legend of the Chessboard is a famous legend that illustrates exponential growth. A courtier presented a Persian king with the chessboard and as a reward the courtier asked the king for a grain of rice in each square of the chessboard, doubling the amount in each new square. The king agreed and gave the courtier 1 grain of rice in the first square, 2 grains of rice in the second, four grains of rice in the third and so on. The king didn’t realize how rapidly the amount of grain of rice would grow in each square. This video would be a great way to engage the students into the topic at the beginning of the lesson. The Legend of the Chessboard shows how rapidly exponential functions can grow. After watching the video the students can try to guess or calculate the total number of grains of rice the courtier would get in the end. Afterwards, the students can then graph the exponential function.

The students can use this website to check their guess:

http://britton.disted.camosun.bc.ca/jbchessgrain.htm

How could you as a teacher create an activity or project that involves your topic?

In order to explore graphing exponential growth and decay functions, the students could play a card sort matching game. The students will work in groups to play the card sort matching game. Some students will be given the graphs and have to use the points given to derive the equation. Some groups will be given the equations and have to create the graphs of the exponential functions. As a class, we will go over graphing exponential growth and decay functions and analyze the graphs. The students will be expected to identify the domain, range, asymptotes, y-intercepts and whether the graph is exponential growth or exponential decay. Also, we could explore how exponential functions compare to other functions that we previously studied. This is a great activity that can be used as review before an exam.

How can this topic be used in your students’ future courses in mathematics or science?

Exponential functions are used to model different real world scenarios involving population, money, finances, bacteria and much more. Students can use exponential functions in other courses such as Calculus, Biology, Chemistry, Physics, and Economics. In calculus, students explore differentiation and integration of exponential functions. Given the position of an object in exponential form, students can use Calculus to determine if the object will stop moving. Newton’s Law of Cooling is an example in physics that demonstrates exponential decay. Compound interest is a major application of exponential functions in finances. Exponential population growth, carbon dating, pH and concentrations of drugs are other examples in math and science that can be modeled by exponential growth and decay functions. In addition, students explore logarithmic functions, the inverses of exponential functions. Being able to recognize and graph exponential growth and decay functions is an important concept that can help students’ in their future courses in math or science.

References:

https://www.youtube.com/watch?v=t3d0Y-JpRRg

http://britton.disted.camosun.bc.ca/jbchessgrain.htm

http://www.shsu.edu/kws006/Precalculus/3.2_Applications_of_Exponential_Functions_files/3.2%20Applications%20of%20Exponential%20Functions%20(slides%204%20to%201).pdf

Engaging students: Using Pascal’s triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Jason Trejo. His topic, from Precalculus: using Pascal’s triangle.

How could you as a teacher create an activity or project that involves your topic?

After some research and interesting observations I came across while examining Pascal’s Triangle, I feel like I could create some sort of riddle worksheet that involves the Triangle. Once I have taught my students how to create Pascal’s Triangle, I could give my students riddles such as:

Once you go and strive in prime, belittling your neighbors isn’t a crime.
- Students might notice that each number (other than 1) in a prime number row is divisible by that prime number:
  - Row 7= 1, 7, 21, 35, 35, 21, 7, 1
  - Row 11= 1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1
- Naturally shallow slides aren’t much fun, but with a fib of raunchy, it is this one.
  - Given that I have gone over the Fibonacci sequence with my students prior to these riddles, I could include this one. The students should eventually see that if you take shallow diagonals on Pascal’s Triangle, the sum of those diagonals are the consecutive numbers in the Fibonacci sequence.
- In a game on blades, you can’t be a schmuck with a puck. Be nimble and quick to look for the stick.
  - This one is a little more straightforward compared to the last two so hopefully the students will make the connection to notice the hockey stick pattern on the diagonals of Pascal’s Triangle. When adding the numbers down a diagonal, then the number to the side and below will be the sum, thus looking like a hockey stick.
- What else is there? What else is in store? What patterns can you find when you know who to root four?
  - The “typo” is intentional to give a hint at another pattern the students might notice on Pascal’s Triangle. Now I am challenging the students to find more patterns within the Triangle such as:
    - Sum of rows are the powers of 2
    - Rows relate to the powers of 11 (get murky after the 4^th row)
    - Counting numbers, triangular numbers, etc.

The purpose of this activity would extend the use of Pascal’s triangle from what they already know. I could assign this at the beginning of the lesson and if no one understands what the riddles meant, we could come back as a class and figure them out together once the lesson was done. These riddles could be an assignment of their own if I introduce them after they are very familiar with Pascal’s Triangle.

How can this topic be used in students’ future courses in mathematics and science?

I would say the primary use most students will get from Pascal’s Triangle would be to find the coefficients of binomials since it is much easier when working on binomial expansions, but there are also other ways they can use the Triangle as well. For one, it can be of great use in many courses that involve since it is a visual in seeing the number of combinations there are based on the number of items used. For example, say there are 6 different pieces of candy in a bowl and you need to know how many different ways can you choose 3 candies? Using Pascal’s Triangle, we look at the 6^th row and the 3^rd entry in that row (remembering the top row is Row 0 and the first 1 in each row is Entry 0), we can see that there are 20 possible combinations of 3 different pieces of candy. Other than that, even based on the riddle activity from above, students can use Pascal’s Triangle and its various patterns to help remember such things as triangular numbers, powers of 11, etc.

How has this topic appeared in high culture?

Within the past few years, the Shanghai-based design company, Super Nature Design, created the interactive art piece “Lost in Pascal’s Triangle”. This structure takes inspiration from Pascal’s Triangle and allows people to “explore the concept and magnification of the Pascal’s Triangle mathematics formula.” The following link takes you to the website that gives a bit more information behind the piece and shows how people can interact with the structure through a xylophone-type console: http://www.supernaturedesign.com/work/pascaltriangle#8

Another quick application that can be done through Pascal’s Triangle is by seeing the relationship between the Triangle and Sierpinski’s triangle (as shown below):

The pattern is by shading in every odd number on Pascal’s Triangle, you start creating Sierpinski’s triangle which is found in many works of art like these:

It might actually be a small but fun project to have the students create something like this at the beginning of the lesson and then explain the relation of the two special triangles.

References:

Pascal Triangle Information: http://jwilson.coe.uga.edu/EMAT6680Su12/Berryman/6690/BerrymanK-Pascals/BerrymanK-Pascals.html

Image of Pascal’s Triangle: http://mathforum.org/workshops/usi/pascal/images/pascal.hex2.gif

Lost in Pascal’s Triangle: http://www.designboom.com/weblog/images/images_2/andrea/super_nature_design/pascaltriangle01.jpg

Super Nature Design: http://www.supernaturedesign.com/work/pascaltriangle#2

Pascal and Sierpinski Triangle : http://mathforum.org/workshops/usi/pascal/images/sierpinski.pascalfrac.gif

Sierpinski Pyramid: http://www.sierpinskitetrahedron.com/images/sierpinski-tetrahedron-breckenridge.JPG

Sierpinski Art Project: http://fractalfoundation.org/wp-content/uploads/2009/03/sierpkids1.jpg

Engaging students: Finding the domain and range of a function

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Esmeralda Sheran. Her topic, from Precalculus: finding the domain and range of a function.

I found that Free Math Help and Khan Academy are both interactive websites that help students learn how to find domain and range of functions. If I were to have a lesson on how to find domain and range of functions I would have my students use the Free Math Help website to explore the concept of domain and range. Using the Free Math Help website a student can input any type of function that they come up with to see what the graph looks like, the steps of how to find the domain/range, and how the domain and range correspond with the graph. I could choose to have students come up with their own functions and they could experiment with expression that are not functions just so they can share some findings they came up on their own. Conversely I could make handouts with a variety of functions both continuous and discrete, expression that are not functions so that I could manage their learning in a way that they can see different graphs and their corresponding domain and ranges. Also I could give them a series of functions with different translations based off of one main parent function.

Then using Khan Academy website I could perform an active elaborate in which the students see a graph and then must give the corresponding domain and range intervals. I can walk around to each student to see what they have recorded and ask them to provide a justification for their answer or explain what properties the graph has that gives the domain and range they come up with. However I chose to structure the activities the students will be able to observe and discuss the changes in the domain and range interactively by using either Khan Academy or Free Math Help.

How can this topic be used in your students’ future courses in mathematics or science?

Knowing how to find domain is fundamental to most any mathematical course proceeding and not excluding pre-calculus. Once students are able to understand how to find the domain and range of a function they are able to learn deeper concepts used in calculus, discrete mathematics, and real analysis. Once in calculus students are expected to use domain and range in order to complete derivative problems specifically pertaining to finding critical points like the maximum/minimum and to describe the function as it changes from interval to interval. Understanding domain and range is also important when students must contrive and solve a definite integral from analyzing a graph or data. Then in discrete mathematics students must apply what they have learned from domain and range in the past to understand what preimage and codomain means and how they relate to the domain and how they differ from range. Apart from the regular mathematic courses, physics, differential equations and similar course also have applications of derivatives and integrals that require previous knowledge on how to find the domain and range of a function.

How could you as a teacher create an activity or project that involves your topic?

I would have the students create maps such as the ones from The Emperor’s New Groove using colored pencils and paper provided in class.
The instructions for the activity would be:
Leave an inch of blank space on the bottom of the page and the left edge.
Then create your own chase scene
- Using two different characters
- Make sure your chase can pass the vertical line test.
Then with rulers use the centimeter side to mark your x and y axis
Now you must find the length and height of each of your chase scenes
- instead of writing 7 cm long; 5 cm high use interval notation [2,9];[1,5]

This activity will help students connect domain and range to being the span of the function’s graph and the possible input and output values. It will be engaging because a kid’s movie is tied into the activity. Also the students can work independently and creatively, which is something different than what they are used to doing in the average classroom. After this activity we could move on to a more in depth discussion of the domain of discrete and discontinuous functions.

References:

The Emperor’s New Groove – Disney Movie

Free Math Help interactive website

http://www.freemathhelp.com/domain-range.html

Khan Academy interactive website

https://www.khanacademy.org/math/algebra/algebra-functions/domain-and-range/e/domain_and_range_0.5

Difference of Two Powers (Part 5)

In this series of posts, I’ve explored ways that students can discover the formula for the difference of two squares and the difference of two cubes:

$x^2 - y^2 = (x-y) (x+y)$

$x^3 - y^3 = (x-y)(x^2 + xy + y^2)$ .

If students have understood the origins of these two formulas, then it’s not much of a stretch for students to guess the formula for $x^4 -y^4$ . A geometric derivation requires four-dimensional visualization which is beyond of what can be reasonably expected of high school students. Still, students can look at the above two formula and guess that $x-y$ is a factor of $x^4-y^4$ , and that the second factor would contain $x^3$ and $y^3$ :

$x^4 - y^4 = (x-y)(x^3 + \hbox{~~~something~~~} + y^3)$ .

From this point forward, it’s a matter of either using long division to find the quotient of $x^4-y^4$ or else just guessing (and confirming) the nature of the $\hbox{something}$ .

Once students recognize that the answer is

$x^4 - y^4 = (x-y)(x^3 + x^2 y + x y^2 + y^3)$ ,

then the factorings of $x^5 - y^5$ , $x^6 - y^6$ , etc. become obvious.

Difference of Two Cubes (Part 4)

Here’s the formula for the difference of two cubes:

$x^3 - y^3 = (x-y)(x^2 + xy + y^2)$

The formula isn’t terribly complicated; however, the factoring on the right-hand side is hardly the first thing that a student would guess if only given the left-hand side to simplify. The formula of course can be confirmed by multiplying out the right-hand side, but that’s really cheating. It’d be nice to have a way for students to develop the right-hand side, as opposed to merely confirming that the right-hand side is correct.

To this end, I suggest using base-10 blocks, a common manipulative found in elementary classrooms. The figure below shows a 10×10 cube with a 3×3 cube removed.

A (hopefully interesting) challenge for students would be how to build this figure only using the materials found in a typical base-10 kit, and also building it with as few pieces as possible. I think that most high school students, after some thought, can solve this puzzle by using 7 flats (for the bottom 7 layers), 21 rods, and 63 units. This of course provides the correct answer, as

$7 \times 100 + 21 \times 10 + 63 \times 1 = 963 = 10^3 - 3^3$ .

After finding the correct answer, students should give this picture some deeper thought. If we let $x = 10$ and $y = 3$ , then

$7 \times 100 = (x-y) x^2$ .

This makes sense on physical grounds: the volume of the “base” of 7 layers is $7 \times 10$ , and the $7$ came from the fact that the top 3 layers are incomplete.

Likewise, the 21 rods can be thought of as

$21 \times 10 = 7 \times 3 \times 10 = (x-y) y x$ .

Again, this makes sense just looking at the picture, as the 21 rods makes a solid that is 3 units high ( $y$ ), 10 units long ( $x$ ), and 7 units wide ( $x-y$ ).

Finally, the 63 units can be thought of as

$63 = 7 \times 3 \times 3 = (x-y) y^2$ .

Indeed, these 63 units form a solid with a square base of side 3 and a length of 7.

Adding them together, we find

$7 \times 100 + 21 \times 10 + 63 \times 1 = (x-y) x^2 + (x-y) xy + (x-y) y^2 = (x-y) (x^2 + xy+ y^2)$ ,

which is indeed the formula for the difference of two cubes. Now that students have discovered the formula for themselves, the formula can then be confirmed using the distributive law.

As a postscript, it should be possible to use two different colors of base-10 blocks (to represent positive and negative numbers) so that students can derive the formula

$x^3 + y^3 = (x+y)(x^2 - xy + y^2)$ .

However, I don’t personally own two different colored base 10 kits, so I haven’t had time to think through how to do this.

Difference of Two Cubes (Part 3)

In my experience, students who have reached the level of calculus or higher have completely mastered the formula for the difference of two squares:

$x^2 -y^2 = (x-y)(x+y)$ .

However, these same students almost never know that there even is a formula for factoring the difference of two cubes $x^3 -y^3$ , and it’s a rare day that I have a student who can actually immediately recall the formula correctly. I suppose that this formula is either never taught in Algebra II or (more likely) students immediately forget the formula after it’s been taught since there’s little opportunity for reinforcing this formula in more advanced courses in mathematics.

I recently came across an interesting pedagogical challenge: Is there an easy way, using commonly used classroom supplies, for teachers to guide students to explore and discover the formula for the difference of two cubes in the same way that they can discover the formula for the difference of two squares? (The cheap way is for students to just multiply out the factored expression to get $x^3 -y^3$ , but that’s cheating since they shouldn’t know what the answer is in advance.)

I came up with a way to do this, and I’ll present it in tomorrow’s post. For now, I’ll leave a thought bubble for anyone who’d like to think about it between now and then.

Difference of Two Squares (Part 2)

In yesterday’s post, I discussed a numerical way for students in Algebra I to guess for themselves the formula for the difference of two squares.

There is a also well-known geometric way of deriving this formula (from http://proofsfromthebook.com/2013/03/20/representing-the-sum-and-difference-of-two-squares/)

The idea is that a square of side $b$ is cut from a corner of a square of side $a$ . By cutting the remaining figure in two and rearranging the pieces, a rectangle with side lengths of $a+b$ and $a-b$ can be formed, thus proving that $a^2 - b^2 = (a+b)(a-b)$ .

Again, this is a simple construction that only requires paper, scissors, and a little guidance from the teacher so that students can discover this formula for themselves.

Difference of Two Squares (Part 1)

In Algebra I, we drill into student’s heads the formula for the difference of two squares:

$x^2 - y^2 = (x-y)(x+y)$

While this formula can be confirmed by just multiplying out the right-hand side, innovative teachers can try to get students to do some exploration to guess the formula for themselves. For example, teachers can use some cleverly chosen multiplication problems:

$9 \times 11 = 99$