Earlier in this series, I gave three different methods of showing that
Using the fact that 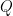 is independent of
is independent of  , I’ll now give a fourth method.
, I’ll now give a fourth method.
 Since
Since 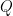 is independent of
is independent of  , I can substitute any convenient value of
, I can substitute any convenient value of  that I want without changing the value of
that I want without changing the value of 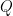 . For example, let me substitute
. For example, let me substitute 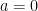 :
:
 Since
Since So that I can employ the magic substitution , I’ll divide the interval of integration into two pieces and then perform the substitution
on the second piece:
One thought on “How I Impressed My Wife: Part 5c”