Area of a triangle: Incenter (Part 6)

John Quintanilla Geometry, Theorems October 6, 2013August 1, 2013 1 Minute

Source: http://mathworld.wolfram.com/Incircle.html

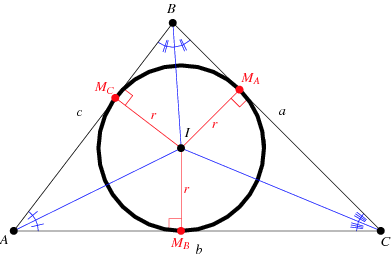
The incenter $I$ of a triangle $\triangle ABC$ is defined by the intersection of the angle bisectors of its three angles. A circle can be inscribed within $\triangle ABC$ , as shown in the picture.

This incircle provides a different way of finding the area of $\triangle ABC$ commonly needed for high school math contests like the AMC 10/12. Suppose that the sides $a$ , $b$ , and $c$ are known and the inradius $r$ is also known. Then $\triangle ABI$ is a right triangle with base $c$ and height $r$ . So

$\hbox{Area of ~} \triangle ABI = \displaystyle \frac{1}{2} cr$

Similarly,

$\hbox{Area of ~} \triangle ACI = \displaystyle \frac{1}{2} br$

$\hbox{Area of ~} \triangle BCI = \displaystyle \frac{1}{2} ar$

Since the area of $\triangle ABC$ is the sum of the areas of these three smaller triangles, we conclude that

$\hbox{Area of ~} \triangle ABC = \displaystyle \frac{1}{2} r (a+b+c)$ ,

or

$\hbox{Area of ~} \triangle ABC = rs$ ,

where $s = (a+b+c)/2$ is the semiperimeter of $\triangle ABC$ .

This also permits the computation of $r$ itself. By Heron’s formula, we know that

$\hbox{Area of ~} \triangle ABC = \sqrt{s(s-a)(s-b)(s-c)}$

Equating these two expressions for the area of $\triangle ABC$ , we can solve for the inradius $r$ :

$r = \displaystyle \sqrt{ \frac{(s-a)(s-b)(s-c)}{s} }$

For much more about the inradius and incircle, I’ll refer to the MathWorld website.

Published by John Quintanilla

I'm a Professor of Mathematics and a University Distinguished Teaching Professor at the University of North Texas. For eight years, I was co-director of Teach North Texas, UNT's program for preparing secondary teachers of mathematics and science. View all posts by John Quintanilla

Published October 6, 2013August 1, 2013

One thought on “Area of a triangle: Incenter (Part 6)”

Pingback: Area of a Triangle and Volume of Common Shapes: Index | Mean Green Math

Leave a comment Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.