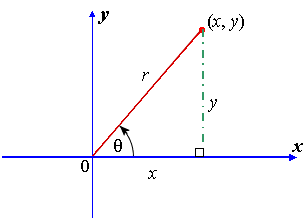How I Impressed My Wife: Part 4d

Previously in this series, I have used two different techniques to show that

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x} = \displaystyle \frac{2\pi}{|b|}.$

Originally, my wife had asked me to compute this integral by hand because Mathematica 4 and Mathematica 8 gave different answers. At the time, I eventually obtained the solution by multiplying the top and bottom of the integrand by $\sec^2 x$ and then employing the substitution $u = \tan x$ (after using trig identities to adjust the limits of integration).

But this wasn’t the only method I tried. Indeed, I tried two or three different methods before deciding they were too messy and trying something different. So, for the rest of this series, I’d like to explore different ways that the above integral can be computed.

Here’s my progress so far:

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

$= \displaystyle \int_0^{2\pi} \frac{2 \, dx}{1+\cos 2x + 2 a \sin 2x + (a^2 + b^2)(1-\cos 2x)}$

$= 2 \displaystyle \int_0^{2\pi} \frac{d\theta}{(1+a^2+b^2) + 2 a \sin \theta + (1 - a^2 - b^2) \cos \theta}$

$= 2 \displaystyle \int_{0}^{2\pi} \frac{d\theta}{S + R \cos (\theta - \alpha)}$

$= 2 \displaystyle \int_{0}^{2\pi} \frac{d\phi}{S + R \cos \phi}$

$= \displaystyle -\frac{4i}{R} \oint_C \frac{dz}{z^2 + 2\frac{S}{R}z + 1}$

$= \displaystyle -\frac{4i}{R} \oint_C \frac{dz}{(z - r_1)(z- r_2)}$

where this last integral is taken over the complex plane on the unit circle, a closed contour oriented counterclockwise. Also,

$r_1 = \displaystyle \frac{-S + \sqrt{S^2 -R^2}}{R}$

and

$r_2 = \displaystyle \frac{-S - \sqrt{S^2 -R^2}}{R}$ ,

are the two distinct roots of the denominator (as long as $b \ne 0$ ). In these formulas, $R = \sqrt{(2a)^2 + (1-a^2-b^2)^2}$ and $S = 1 + a^2 + b^2$ . (Also, $\alpha$ is a certain angle that is now irrelevant at this point in the calculation).

This contour integral looks more complicated; however, it’s an amazing fact that integrals over closed contours can be easily evaluated by only looking at the poles of the integrand. For this integral, that means finding the values of $z$ where the denominator is equal to 0, and then determining which of those values lie inside of the closed contour.

Let’s now see if either of the two roots of the denominator lies inside of the unit circle in the complex plane. In other words, let’s determine if $|r_1| < 1$ and/or $|r_2| < 1$ .

I’ll begin with $r_1$ . Clearly, the numbers $R$ , $\sqrt{S^2-R^2}$ , and $S$ are the lengths of three sides of a right triangle with hypotenuse $S$ . So, since the hypotenuse is the longest side,

$S > \sqrt{S^2-R^2}$

$0 > -S + \sqrt{S^2-R^2}$

so that

$0 > \displaystyle \frac{-S + \sqrt{S^2-R^2}}{R}$ .

Also, by the triangle inequality,

$R + \sqrt{S^2 - R^2} > S$

$-S + \sqrt{S^2 - R^2} > -R$

$\displaystyle \frac{-S + \sqrt{S^2-R^2}}{R} > -1$

Combining these inequalities, we see that

$-1 < \displaystyle \frac{-S + \sqrt{S^2-R^2}}{R} < 0$ ,

and so I see that $|r_1| < 1$ , so that $r_1$ does lie inside of the contour $C$ .

The second root $r_2$ is easier to handle:

$|r_2| = \left| \displaystyle \frac{-S - \sqrt{S^2 -R^2}}{R} \right| = \left| \displaystyle \frac{S + \sqrt{S^2 -R^2}}{R} \right| > \displaystyle \frac{S}{R} > 1$ .

Therefore, since $r_2$ lies outside of the contour, this root is not important for the purposes of computing the above contour integral.

Now that I’ve identified the root that lies inside of the contour, I now have to compute the residue at this root. I’ll discuss this in tomorrow’s post.

How I Impressed My Wife: Part 4c

Previously in this series, I have used two different techniques to show that

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x} = \displaystyle \frac{2\pi}{|b|}.$

Here’s my progress so far:

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

$= \displaystyle \int_0^{2\pi} \frac{2 \, dx}{1+\cos 2x + 2 a \sin 2x + (a^2 + b^2)(1-\cos 2x)}$

$= 2 \displaystyle \int_0^{2\pi} \frac{d\theta}{(1+a^2+b^2) + 2 a \sin \theta + (1 - a^2 - b^2) \cos \theta}$

$= 2 \displaystyle \int_{0}^{2\pi} \frac{d\theta}{S + R \cos (\theta - \alpha)}$

$= 2 \displaystyle \int_{0}^{2\pi} \frac{d\phi}{S + R \cos \phi}$

$= \displaystyle -\frac{4i}{R} \oint_C \frac{dz}{z^2 + 2\frac{S}{R}z + 1}$ ,

where this last integral is taken over the complex plane on the unit circle, a closed contour oriented counterclockwise. Also, $R = \sqrt{(2a)^2 + (1-a^2-b^2)^2}$ and $S = 1 + a^2 + b^2$ (and $\alpha$ is a certain angle that is now irrelevant at this point in the calculation).

To begin, we use the quadratic formula to find the roots of the denominator:

$z^2 + 2\frac{S}{R}z + 1 = 0$

$Rz^2 + 2Sz + R = 0$

$z = \displaystyle \frac{-2S \pm \sqrt{4S^2 - 4R^2}}{2R}$

$z = \displaystyle \frac{-S \pm \sqrt{S^2 -R^2}}{R}$ .

So we have the two roots $r_1 = \displaystyle \frac{-S + \sqrt{S^2 -R^2}}{R}$ and $r_2 = \displaystyle \frac{-S - \sqrt{S^2 -R^2}}{R}$ . Earlier in this series, I showed that $S > R > 0$ as long as $b \ne 0$ , and so the denominator has two distinct real roots. So the integral $Q$ may be rewritten as

$Q = \displaystyle -\frac{4i}{R} \oint_C \frac{dz}{(z - r_1)(z- r_2)}$

Next, we have to determine if either $r_1$ or $r_2$ (or both) lies inside of the contour. I’ll discuss this in tomorrow’s post.

Proving theorems and special cases (Part 11): The Law of Cosines

In a recent class with my future secondary math teachers, we had a fascinating discussion concerning how a teacher should respond to the following question from a student:

Is it ever possible to prove a statement or theorem by proving a special case of the statement or theorem?

Usually, the answer is no. In this series of posts, we’ve seen that a conjecture could be true for the first 40 cases or even the first $10^{316}$ cases yet not always be true. We’ve also explored the computational evidence for various unsolved problems in mathematics, noting that even this very strong computational evidence, by itself, does not provide a proof for all possible cases.

However, there are plenty of examples in mathematics where it is possible to prove a theorem by first proving a special case of the theorem. For the remainder of this series, I’d like to list, in no particular order, some common theorems used in secondary mathematics which are typically proved by first proving a special case.

2. Theorem. In $\triangle ABC$ where $a = BC$ , $b = AC$ , and $c = AB$ , we have $c^2 = a^2 + b^2 - 2 a b \cos (m \angle C)$ .

This is typically proven using the Pythagorean theorem:

Lemma. In right triangle $\triangle ABC$ , where $\angle C$ is a right angle, we have $c^2 = a^2 + b^2$ .

Though it usually isn’t thought of this way, the Pythagorean theorem is a special case of the Law of Cosines since $\cos 90^\circ = 0$ .

There are well over 100 different proofs of the Pythagorean theorem that do not presuppose the Law of Cosines. The standard proof of the Law of Cosines then uses the Pythagorean theorem. In other words, a special case of the Law of Cosines is used to prove the Law of Cosines.

Another proof of the Pythagorean theorem

Source: https://www.facebook.com/AmerMathMonthly/photos/a.250425975006394.53155.241224542593204/737392972976356/?type=1&theater

Engaging students: Verifying trigonometric identities

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Michelle McKay. Her topic, from Precalculus: verifying trigonometric identities.

How could you as a teacher create an activity or project that involves your topic?

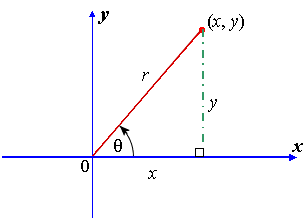
Engaging students with trigonometric identities may seem daunting, but I believe the key to success for this unit lies within allowing students to make the discovery of the identities themselves.

For this particular activity, I will focus on some trigonometric identities that can be derived using the Pythagorean Theorem. Before beginning this activity, students must already know about the basic trig functions (sine, cosine, and tangent) along with their corresponding reciprocals (cosecant, secant, and cotangent).

Using this diagram (or a similar one), have students write out the relationship between all sides using the Pythagorean Theorem.
Students should all come to the conclusion of: x² + y² = r².

For higher leveled students, you may want to remind them of the adage SohCahToa, with emphasis on sine and cosine for this next part. You might ask, “How can we rearrange the above equation into something remotely similar to a trigonometric function?”

Ultimately, we want students to divide each side by r². This will give us:

Again, SohCahToa. Students, perhaps with some leading questions, should see that we can substitute sine and cosine functions into the above equation, giving us the identity:

cos²θ + sin²θ = 1

From this newly derived identity, students can then go on to find tan²θ + 1 = sec²θand then 1 + cot²θ = csc²θ.

How can technology be used to effectively engage students with this topic?

For engaging the students and encouraging them to play around with identities, I find the Trigonometric Identities Solver by Symbolab to be a fabulous technological supplement. Students can enter in identities that they may need more help understanding and this website will state whether the identity is true or not, and then provide detailed steps on how to derive the identity.
A rather fun activity that may utilize this site is to challenge the students to come up with their own elaborate trigonometric identity.

Another online tool students can explore is the interactive graph from http://www.intmath.com. In fact, students could also use this right after they derive the identities from the earlier activity. This site does a wonderful job at providing a visual representation of the trigonometric functions’ relationships to one another. It also allows the students to explore the functions using concrete numbers, rather than the general Ө. Although this site only shows the cos²θ + sin²θ = 1identity in action, it would not be difficult for students to plug in the data from this graph to numerically verify the other identities.

What are the contributions of various cultures to this topic?

The beginning of trigonometry began with the intention of keeping track of time and the quickly expanding interest in the study of astronomy. As each civilization inherited old discoveries from their predecessors, they added more to the field of trigonometry to better explain the world around them. The below table is a very brief compilation of some defining moments in trigonometry’s history. It is by no means complete, but was created with the intention to capture the essence of each civilization’s biggest contributions.

Civilization	People of Interest	Contributions
Egyptians	Ahmes	– Earliest ideas of angles.- The Egyptian seked was the cotangent of an angle at the base of a building.
Babylonians		– Division of the circle into 360 degrees.- Detailed records of moving celestial bodies (which, when mapped out, resembled a sine or cosine curve).- May have had the first table of secants.
Greek	Aristarchus Menelaus Hippocharus Ptolemy	– Chords.- Trigonometric proofs presented in a geometric way.- First widely recognized trigonometric table: Corresponding values of arcs and chords.- Equivalent of the half-angle formula.
Indian	Aryabhata Bhaskara I Bhaskara II Brahmagupta Madhava	– Sine and cosine series.- Formula for the sine of an acute angle.- Spherical trigonometry.- Defined modern sine, cosine, versine, and inverse sine.
Islamic	Muhammad ibn Mūsā al-Khwārizmī Muhammad ibn Jābir al-Harrānī al-Battānī Abū al-Wafā’ al-Būzjānī	– – First accurate sine and cosine tables.- – First table for tangent values.- – Discovery of reciprocal functions (secant and cosecant).- – Law of Sines for spherical trigonometry.- – Angle addition in trigonometric functions.
Germans		– “Modern trigonometry” was born by defining trigonometry functions as ratios rather than lengths of lines.

It is interesting to note that while the Chinese were making many advances in other fields of mathematics, there was not a large appreciation for trigonometry until long after they approached the study and other civilizations had made significant contributions.

Sources

Proof without words: Pythagoras for a clipped rectangle

Source: https://www.facebook.com/photo.php?fbid=494951053971731&set=a.416585131808324.1073741827.416199381846899&type=1&theater

Pythagorean quadruplets

Source: https://www.facebook.com/photo.php?fbid=494942050639298&set=a.416585131808324.1073741827.416199381846899&type=1&theater

Engaging students: Deriving the Pythagorean Theorem

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Michelle McKay. Her topic, from Geometry: deriving the Pythagorean Theorem.

How could you as a teacher create an activity or project that involves your topic?

Below I have attached an activity that I like to call “Being Pythagoras for a Day”. To summarize the activity, students are given instructions (with a few guiding images) that leads them to physically manipulate various shapes that demonstrate the relationship between the sides of a right triangle. By the instructions, students will derive the Pythagorean Theorem on their own and come to understand why each side in the equation is squared. Let it be noted that the title of this activity is not just a gimmick. The proof the students will work on in this activity is the same as the one Pythagoras was given credit for using.

Michelle_McKay_BeingPythagorasForADay_A

How has this topic appeared in the news?

Not even a year ago to this day, Coach Jason Garrett of the Dallas Cowboys made a splash in the world of sports and math with his unusual demands of his players: they needed to have a sound understanding of Geometry, including the Pythagorean Theorem. Garrett fully believes that players must understand the Pythagorean Theorem to make better decisions out on the field. The following quote was taken from an interview where Garrett discusses why he feels being familiar with the Pythagorean Theorem can prevent a poor decision:

“If you’re running straight from the line of scrimmage, six yards deep, that’s a certain depth, right? It takes you a certain amount of time. But if you’re doing it from 10 yards inside and running to that same six yards, that’s the hypotenuse of that right triangle. It’s longer, right? So they have to understand that, that it takes longer to do that. That’s an important thing. Quarterbacks need to understand that, too. If you’re running a route from here to get to that spot, it’s going to be a little longer, you might need to be a little fuller in your drop.”

Let this be a wakeup call for everyone who wants to become a professional football player and never thought they would have to use the Pythagorean Theorem outside of high school!

What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?
People can easily recognize the Egyptian pyramids as one of the wonders of the world. What is not often discussed is how the engineers and architects of the day used the Pythagorean Theorem to lay the pyramids’ foundations correctly. Those primarily responsible for the pyramids’ construction were called “rope-stretchers”. This name came from the inventive method of tying thirteen, evenly spaced knots into a rope. When the rope was pegged to the ground, a 3-4-5 triangle was produced. This allowed them to accurately and consistently map out the bases of the pyramids.

Some argue that the rope-stretchers fully understood the Pythagorean Theorem and used that knowledge to manipulate the ropes, while others argue that they were intuitively using the properties of a right triangle. Due to this area of ambiguity, it is unclear whether Pythagoras was taught the theorem by the Egyptians first, or if, through watching the process, he was able to discover the relationship of a right triangle’s sides on his own.

Interestingly enough, there exist various pieces of artwork depicting Egyptians holding ropes and using them for measurement. Just by looking at the images, it is not clear if the ropes are being used for the construction of the pyramids or for dividing land (another event where the knotted ropes were used to fairly distribute plots of land).

Sources:

Paths

I offer the following xkcd comic as a possible engagement exercise concerning the Pythagorean theorem.

Source: http://www.xkcd.com/85/

Football and the hypotenuse

An amusing video from Training Camp 2013 for illustrating that each side of a triangle (including right triangles) is shorter than the sum of the other two sides. The speaker is Jason Garrett, head coach of the Dallas Cowboys.