Inverse functions: Square root (Part 1)

What is the math question that can be stated in two seconds but is most often answered incorrectly by math majors? In my opinion, here it is:

Simplify $\sqrt{x^2}$ .

In my normal conversational voice, I can say “Simplify the square root of $x$ squared” in a shade less than two seconds.

Here’s a thought bubble if you’d like to think about this before I give the answer.

A common mistake made by algebra students (and also math majors in college who haven’t thought about this nuance for a while) is thinking that $\sqrt{x^2} = x$ . This is clearly incorrect if $x$ is negative:

$\sqrt{(-3)^2} = \sqrt{9} = 3 \ne -3$

The second follow-up mistake is then often mistake made by attempting to rectify the first mistake by writing $\sqrt{x^2} = \pm x$ . The student usually intends the symbol $\pm$ to mean “plus or minus, depending on the value of $x$ ,” whereas the true meaning is “plus or minus” without any caveats. I usually correct this second mistake by pointing out that when a student finds $\sqrt{9}$ with a calculator, the calculator doesn’t flash between $3$ and $-3$ ; it returns only one answer.

After clearing that conceptual hurdle, students can usually guess the correct simplification:

$\sqrt{x^2} = |x|$

In this series of posts, I’d like to expand on the thoughts above to consider some of the inverse functions that commonly appear in secondary mathematics: the square-root function and the inverse trigonometric functions.

Engaging students: Inverse Functions

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Allison Myers. Her topic, from Algebra II: inverse functions.

CURRICULUM

How can this topic be used in your students’ future courses in mathematics or science?

Functions are a composition of one or more actions that maps one object onto another (each input maps to one output). Inverse functions are a composition of reverse actions that “undo” the actions of the original function.

Inverse functions have real-world applications, but also students will use this concept in future math classes such as Pre-Calculus, where students will find inverse trigonometric functions. Inverse trigonometric functions have a whole new set of real-world applications, such as finding the angle of elevation of the sun, or anything which models harmonic motion.

Students will also see this concept again in Calculus, where they will differentiate inverse trigonometric functions to solve real-world applications involving rate of angular rotation or the rate of change of angular size.

TECHNOLOGY

How can technology be used to effectively engage students with this topic?

In the past, I taught a lesson where the Explore portion of the lesson utilized dry erase markers and transparency sheets to allow students to discover what happens graphically when computing an inverse (trigonometric) function. My goal was for my students to understand why we compute inverses the way we do. To my horror, my theoretical 15-minute, super insightful Explore became messy, full of problems, and confusing to my students.

While reflecting after the lesson, I began to consider how using technology would have better served my students (in their understanding) and myself (in my goals for the lesson). I found Glencoe’s directions for using the TI-Nspire to compute inverse functions (see image below). Using the TI-Nspire, I would start the lesson with a real-world example and data and have my students complete Step 1. Next, I would explain our need to “undo/reverse” the data, and allow the students to come up with different ways to do so. After that, I would ask the students to make conjectures about possible formulas. Using the TI-Nspire would be less messy and time-consuming (as compared to my experience with markers and transparencies), and would also allow the teacher to be within the context of a real-world problem. I believe if we used this (or similar) technology, combined with the constructivist-style teaching, students would come away with not only a better understanding for computing inverse functions but also their real-world applications.

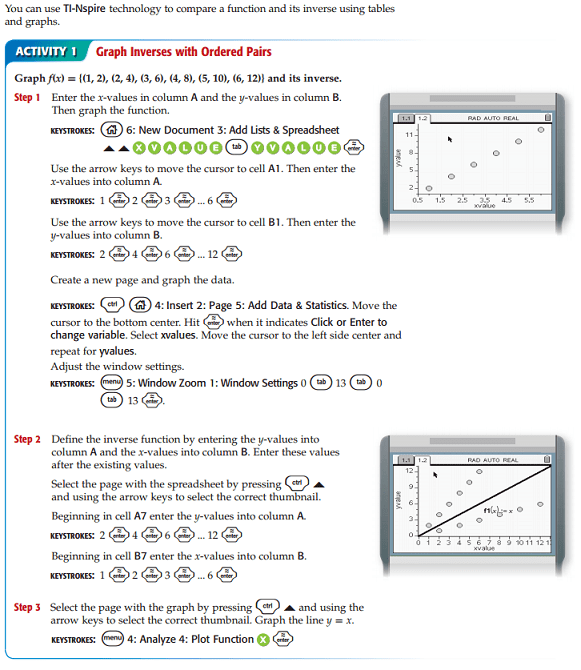Source: http://glencoe.com/sites/common_assets/mathematics/alg2_2010/other_cal_keystrokes/TI-Nspire/Nspire_423_424_C07L2B_888482.pdf

CULTURE

How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?

Inverse functions are used every day in real life. For example, when a computer reads a number you type in, it converts the number to binary for internal storage, then it prints the number out again onto the screen that you see – it’s utilizing an inverse function. A basic example involves converting temperature from Fahrenheit to Celsius.

Another example, if one considers music notes on paper to be a function of the sound produced, then the software Sibelius can be considered the inverse function, as it takes a musician’s music and converts it back to music notes.

Engaging students: Computing inverse functions

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Derek Skipworth. His topic, from Algebra II: computing inverse functions.

B. How can this topic be used in your students’ future courses in mathematics or science?

In essence, an inverse function is supposed to “undo” what the original function did to the original input. Knowing how to properly create inverse functions gives you the ultimate tool for checking your work, something valuable for any math course. Another example is Integrals in Calculus. This is an example of an inverse operation on an existing derivative. A stronger example of using actual inverse functions is directly applied to Abstract Algebra when inverse matrices are needed to be found.

C. How has this topic appeared in high culture?

The idea of inverse functions can be found in many electronics. My hobby is 2-channel stereo. Everyone has stereos, but it is viewed as a “higher culture” hobby when you get into the depths that I have reached at this point. One thing commonly found is Chinese electronics. How does this correlate to my topic? Well, the strength of the Chinese is that they are able to offer very similar products comparable to high-end, high-dollar products at a fraction of the costs. While it is true that they do skimp on some parts, the biggest reason they are able to do this is because of their reverse engineering. Through reverse engineering, they do not suffer the massive overhead of R&D that the “respectable” companies have. Lower overhead means lower cost to the consumer. Because of the idea of working in reverse, “better” products are available to the masses at cheaper prices, thus improving the opportunity for upgrades in 2-channel.

E. How can technology be used to effectively engage students with this topic?

A few years ago, there was a game released on Xbox 360 arcade called Braid. It was a commercial and critical success. The gameplay was designed around a character who could reverse time. The trick was that there were certain obstacles in each level that prevented the character from reversing certain actions. To tie technology into a lesson plan, I would choose a slightly challenging level and have the class direct me through the level. This would tie into a group activity where the students are required to calculate inverse functions to reverse their steps (like Braid) and eventually solve a “master” problem that would complete the activity. This activity could be loosely based off a second level that could wrap up the class based off the results that each group produced from the activity.

http://braid-game.com/