Is 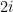 less than
less than 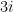 ?
?
That’s a very natural question for a student to ask when first learning about complex numbers. The short answer is, “No… there isn’t a way to define inequality for complex numbers that satisfies all the properties of real numbers.”
However, for this answer to make sense, we need to talk about how inequalities are defined in the first place.
Following Apostol’s calculus, there are four axioms from which the ordinary notions of inequality follow. We shall assume that there exists a certain subset 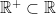 , called the set of positive numbers, which satisfies the following four order axioms:
, called the set of positive numbers, which satisfies the following four order axioms:
- If
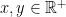 , then
, then 
- If
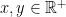 , then
, then  .
.
- For every real
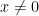 , either
, either 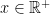 or
or 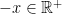 , but not both.
, but not both.
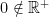
We then define the symbols 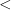 ,
,  ,
, 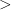 , and
, and 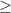 in the obvious way:
in the obvious way:
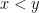 means that
means that  is positive.
is positive. means that $y < x$.
means that $y < x$.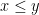 means that either
means that either 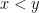 or
or  .
. means that
means that 
From only these four axioms, many familiar theorems about inequalities can be proven. For what it’s worth, when I was a student in Algebra I, I had to prove nearly all of these theorems.
- If
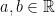 , then exactly one of the following three relations is true:
, then exactly one of the following three relations is true:  ,
,  ,
,  .
.
- If
 and
and  , then
, then  .
.
- If
 , then
, then 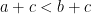 .
.
- If
 and
and  , then
, then  .
.
- If
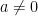 , then
, then  .
.
 .
.
We interrupt this list with a public-service announcement: Yes, there’s a proof that  is greater than
is greater than  . When I tell this to students, I can usually see their heads start to spin, as they think, “Of course we know that!” Then I ask them what the definitions of
. When I tell this to students, I can usually see their heads start to spin, as they think, “Of course we know that!” Then I ask them what the definitions of  and
and  are. Usually, they have no idea. Then I’ll remind them that
are. Usually, they have no idea. Then I’ll remind them that  is defined to be the additive identity (so that
is defined to be the additive identity (so that  and
and 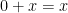 for all real numbers
for all real numbers  ), while
), while  is defined to be the multiplicative identity (so that
is defined to be the multiplicative identity (so that  and
and  for all real numbers
for all real numbers  ). Based on those definitions alone, I then ask my students, is it obvious that the multiplicative identity has to be larger than the additive identity? The answer is no, which is why the above order axioms are needed.
). Based on those definitions alone, I then ask my students, is it obvious that the multiplicative identity has to be larger than the additive identity? The answer is no, which is why the above order axioms are needed.
Here are some more familiar theorems about inequalities that derive from the four order axioms.
- If
 and
and 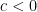 , then
, then 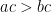 .
.
- If
 , then
, then  .
.
- If
 , then
, then  .
.
- If
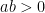 , then
, then  and
and 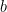 are either both positive or both negative.
are either both positive or both negative.
- If
 and
and 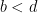 , then
, then  .
.
- If
 and
and  , then
, then  .
.
- If
 , then
, then  .
.
- If
 , then
, then  .
.
- If
 , then
, then  .
.
- If
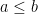 and
and 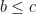 , then
, then 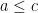 .
.
- If
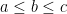 and
and  , then
, then 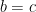 .
.
These last two theorems are less familiar. They basically state that (1) there is no “biggest” real number and (2) there is no positive number that’s immediately to the right of 0.
- There is no real number
 so that
so that  for all real numbers
for all real numbers  .
.
- If
 for every positive real number
for every positive real number 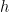 , then
, then  .
.

Here’s another important theorem that ultimately derives from the four order axioms, proving that a number system including 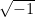 is incompatible with the four order axioms.
is incompatible with the four order axioms.
- There is no real number
 so that
so that 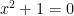 .
.
The proof of this theorem is simple, given the theorems above. If  , then
, then 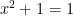 , which is greater than 0. If
, which is greater than 0. If 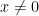 , then
, then 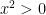 , and so
, and so  . Since
. Since  , it follows by transitivity that
, it follows by transitivity that 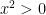 . Either way,
. Either way, 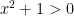 , and so
, and so 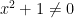 .
.
 Previously in this series, I have used two different techniques to show that
Previously in this series, I have used two different techniques to show that
,
and
. (Also,
is a certain angle that is now irrelevant at this point in the calculation).
.
times the sum of the residues within the contour; see Wikipedia and Mathworld for more information.
