Engaging students: Finding the equation of a circle

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Tiffany Wilhoit. Her topic, from Precalculus: finding the equation of a circle.

How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)? How has this topic appeared in high culture (art, classical music, theatre, etc.)?

Circles are found everywhere! Everyday, multiple times a day, people come across circles. They are found throughout society. The coins students use to buy sodas are circles. On the news, we hear about crop circles and circular patterns in the fields around the world. One of the first examples of a circle was the wheel. Many logos for large companies involve circles, such as Coca-Cola, Google Chrome, and Target. Even the Roman Coliseum is circular in shape. Since circles are found everywhere, students will be able to identify and be comfortable with the shape (more than say a hexagon). A great way to get the students engaged in the topic of circles would be to have the brainstorm different places they see circles on a normal day. Then have each student pick an example and print or bring a picture of it. Then have the student take their circle (say the Ferris Wheel of the state fair), and place in centered at the origin. The students could then find the equation of their circle. They could do another example where their circle is centered at another point as well. This would allow the students to become more aware of circles around them, and would also allow them some freedom in the assignment.

What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?

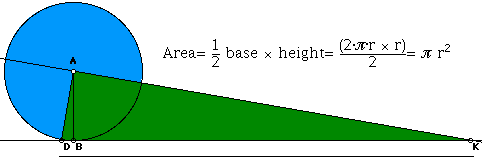
Circles have been an interesting topic for humans since the beginning. We see the sun as a circle in the sky. The ancient Greeks even believed the circle was the perfect shape. Ancient civilizations built stone circles such as Stonehenge, and circular structures such as the Coliseum. The circle led to the invention of the wheel and gears, as well. The study of geometry is focused largely around the study of circles. The study of circles led to many inventions and ideas. Euclid studied circles, and compared them to other polygons. He found ways to create circles that could circumscribe and inscribe polygons. This created a problem called “squaring a circle”. Ancient Greeks tried to construct a circle and square with the same area using only a compass and straightedge. The problem was never solved, but in 1882 it was proved impossible. However, people still tried to solve the problem and were called “circle squarers”. This became an insult for people who attempted the impossible. Borromean Rings is another puzzle involving circles. Circles have been a part of civilization from the beginning, and it is amazing how much they are still prevalent today.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

The website on www.mathopenref.com/coordgeneralcircle.html is a good site to use when learning to find the equation of a circle. The page contains an applet where the students are able to work with a circle. The circle can be moved so the center is at any point, and the radius can be changed to various sizes. At the top, it shows the equation of the circle shown. This website would allow the students to see how the equation of a circle changes depending on the center and size. This is a good tool to use for the students to explore circles and their equations or to review them before the test. The website also contains some information for the students to read to understand the concept, and there is even an example to try. The website is easy to use, and would not be difficult for students to understand.

Resources:

http://www-history.mcs.st-and.ac.uk/Curves/Circle.html

http://nrich.maths.org/2561

www.mathopenref.com/coordgeneralcircle.html

https://circlesonly.wordpress.com/category/history-of-circles/

Circumference

Source: http://www.xkcd.com/1184/

Further comments, from Nicholas Vanserg, “Mathmanship,” The American Scientist, Vol. 46, No. 3 (1958):

In an article published a few years ago, the writer intimated with befitting subtlety that since most concepts of science are relatively simple (once you understand them), any ambitious scientist must, in self-preservation, prevent his colleagues from discovering that his ideas are simple too…

The object of… Mathmanship is to place unsuspected obstacles in the way of the pursuer until he is obliged, by a series of delays and frustrations, to give up the chase and concede his mental inferiority to the author…

[U]se a superscript as a key to a real footnote. The knowledge seeker reads that $S$ is $-36.7^{14}$ calories and thinks, “Gee what a whale of a lot of calories,” until he reads to the bottom of the page, finds footnote 14 and says, “oh.”

Mathematical Christmas gifts

Now that Christmas is over, I can safely share the Christmas gifts that I gave to my family this year thanks to Nausicaa Distribution (https://www.etsy.com/shop/NausicaaDistribution):

Euler’s equation pencil pouch:

Box-and-whisker snowflakes to hang on our Christmas tree:

And, for me, a wonderfully and subtly punny “Confidence and Power” T-shirt.

Thanks to FiveThirtyEight (see http://fivethirtyeight.com/features/the-fivethirtyeight-2014-holiday-gift-guide/) for pointing me in this direction.

For the sake of completeness, here are the math-oriented gifts that I received for Christmas:

Area of a Circle: Index

I’m using the Twelve Days of Christmas (with a week-long head start) to do something that I should have done a long time ago: collect past series of posts into a single, easy-to-reference post. The following posts formed my series on the formula for the area of a circle.

Part 1: Why the circumference function $C(r) = 2 \pi r$ is the derivative of the area function $A(r) = \pi r^2$ .

Part 2: Finding the area of a circle via integration by trigonometric substitution.

Part 3: Finding the area of a circle via a double integral.

Part 4: Justifying the formula $A(r) = \pi r^2$ to geometry students by slicing a circle into pieces and rearranging the pieces as a parallelogram (approximately).

Happy Thanksgiving!

Source: http://politicalcalculations.blogspot.com/2011/11/happy-thanksgiving.html#.U-wl6GOrL5x

Engaging students: Finding the equation of a circle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Billy Harrington. His topic, from Precalculus: finding the equation of a circle.

1) Word problems that have to do with landscaping always seem to engage the students that I am teaching. I would ask a question about a garden, a fountain, or even a gazebo. There are a variety of questions you can ask them about these topics, such as finding the total land (total area) this certain object of scenery would occupy on this piece of land pre-determined. You can even ask for different attributes of the circle if you give say the radius, diameter, or circumference, then the students can find the rest of the characteristics of the circle. Place the objects on a Cartesian coordinate plane and tell the students to identify the characteristics of the circle, and identify the radius and points of the circle to identify and discover the radius of the circle.

2) For a full activity, I would give students a cut of out regular geometric shapes that represent different characteristics of a landscaping project. Each geometric figure represents an object that is being considered for the final product. The problem is below.

Lord Quintanilla request from the local landscaping firm called “Class of 4050”, that he want a new circular house to retire in and spend the rest of his life in with his family. His lot size is rectangular (represents the Cartesian plane), however, he wants his house to be circular. Help Lord Quintanilla find the dimensions of his house by finding the equation of the circular house on a Cartesian coordinate plane. He wants his new house to have at least 2500 square feet. Help him find the radius, and best location.

1) Students use area in their curriculum in geometry and any upper level math classes that deal with shapes. A big topic in calculus that deals with circles is related rates. Students must understand each and every formula that deals with a circle, and they must know how to alter and manipulate each formula to fit the related rates problem. Another big section that circles are used is conics. Students must find the equation of a circle. When students are given the area of a circle, they must find the characteristics of the circle and label where the center is and find out exactly what the radius equals.

2) Students learn the actual equation of a circle in algebra 2, however, once students learn the equation of a circle, then they can re-visit the circle sections of geometry and apply the topics to find the equations of all the different circles. To alter and make the topic more difficult, change the radius length or even change where the center of the circle is. This will help elicit higher level thinking to help students determine the changes to the equation.

1) Students can use technology by using either their calculators or even by using their computers to graph and calculate the different characteristics of the circle. A great website to show circle characteristics is http://www.geogebra.com . This website is a great geometry website that shows many of the characteristics of the shape. Using this website, it can show how different characteristics of the circle, such as the radius or circumference are changed, when you increase or decrease the diameter. This website is a great website to visually show how a circle is altered when you change one of the measurements of the circle.

Engaging students: Radius, diameter, and circumference of circles.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Nataly Arias. Her topic, from Geometry: the radius, diameter, and circumference of circles.

D3. How did people’s conception of this topic change over time?

In order to calculate the circumference of a circle we must multiply the diameter by . The diameter of a circle is the length of the line through the center and touching two points on its edge. In simpler terms the diameter is two times the radius. To get the circumference of a circle we have to work with its radius or diameter and . So the more important question is, what is and how does it relate to circles? Pi or π is a mathematical constant which represents the ratio of any circle’s circumference to its diameter in Euclidean geometry. It is the same as the ratio of a circle’s area to the square of its radius. This can be seen as far back as 250 BCE in the times of Archimedes. Archimedes wrote several mathematical works including the measurement of a circle. Measurement of the circle is a fragment of a longer work in which is shown to lie between the limits of $3 \frac{10}{71}$ and $3 \frac{1}{7}$ . His approach to determining consisted on inscribing and circumscribing regular polygons with a large number of sides. His approach was followed by everyone until the development of infinite series expansions in India during the 15^th century and the 17^th century in Europe. The circumference of circles was found in the works of Archimedes and is now reflected in our math textbooks. This topic has been seen for many centuries and is still seen today. It has become an important part of math and has become an important part of the mathematics curriculum in schools.

E1. How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers, Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

If I was teaching a middle school class on radius, diameter, and circumference of circles I would incorporate technology in my lesson. I have seen firsthand how effective technology can be when teaching your students. I showed the class a video clip during the lesson. As soon as I pulled down the screen projector they sat up, their eyes lit up and they were excited. This is why I have chosen this video clip from YouTube for this particular topic. I think it’s important to change it up and not always stick to a particular teaching style. Some students learn more visually and watching a video instead of listening to a lecture might be more entertaining for students. I know that teachers can’t rely on only technology to teach their students but using things like YouTube can certainly help and be beneficial. I chose this clip because I liked that it used and went over several examples and related circles to things students see every day like a pizza, tire, and table. I also like that it went over definitions in a clear and easy to understand way for students. It explained what a radius and diameter is and how to find it. This helpful video discusses the calculation of the circumference and its area. It also explains the relationship between and the circumference. This 8 minute clip could be used as part of your explain section of your lesson or could even be used to help students review the topic before a test or quiz.

D4. What are the contributions of various cultures to this topic?

When dealing with the radius, diameter, and the circumference of circles there is no escaping pi. Pi represents the ratio of any circle’s circumference to its diameter and is one of the most important mathematical constants. It’s used in many formulas from mathematics, engineering, and science. In math we use to solve for the circumference of a circle with formula $C=2\pi r$ . Sometime in early history someone discovered the relationship between the size of the circumference and the diameter of all circles was a constant ratio. This was seen and presented in the earliest recorded mathematical documents of Babylon and Egypt over 2000 years ago. At this time they did not use the symbol that we use today it wasn’t till much later. They had established that the ratio was equal to $\frac{C}{D}$ , where C is the circumference and D is the diameter of any given circle. At this stage, the Egyptian and Babylonian mathematicians came up with numerical approximations to $\frac{C}{D}$ which is the number we now call pi. Their methods are still unclear and unknown today. In their time period there was no modern number system. They didn’t even have pencil and paper. It has been predicted that they used a rope and sticks to draw circles in the sand and that they also used the rope to measure how many diameters made up a circumference of a circle.

References

http://www.britannica.com/EBchecked/topic/458986/pi

http://www.britannica.com/EBchecked/topic/32808/Archimedes

http://www.youtube.com/watch?v=Yb1HYyBfLfc

http://www.ms.uky.edu/~lee/ma502/pi/MA502piproject.html

http://www.ams.org/samplings/feature-column/fc-2012-02

Engaging students: Circumference of a circle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Daniel Littleton. His topic, from Geometry: computing the circumference of a circle.

C3: How has this topic appeared in the news?

On January 29, 2014 an internet based publisher of medical news, news-medical.net, published an article as to the link between waist circumference and health risk factors. The article is entitled Waist Circumference Measurements Help to Detect Children and Adolescents with Cardiometabolic Risk. This study was conducted in Spain and concluded that including the measurement of waist circumference in clinical practices, in conjunction with traditional height and weight measurements, will allow an easier detection of risk factors for cardiometabolic disorders in children. Waist circumference is measured by placing a tape measure at the top of the hip bone and wrapping the tape around the body level with the navel. This measurement is the circumference, and this measurement can be used to determine the radius and diameter of a human body by knowing that circumference is equivalent to $2 \pi r$ where $r$ is the radius of the circle. This is certainly not the first use of waist circumference in determining health risk factors published in a medical article, however this is a very recent example. This story may be found at the following link: http://www.news-medical.net/news/20140129/Waist-circumference-measurements-help-to-detect-children-and-adolescents-with-cardiometabolic-risk.aspx.

A1: What interesting word problems using this topic can your students do now?

One example of an engaging word problem utilizing the concept of a circumference is as follows. “Aliens have invaded earth and they are establishing colonies on Earth. You are a member of the human resistance and you need to plant explosive traps for the alien soldiers. You know that you have enough materials to build one large bomb, one mid-size bomb, and one small bomb. The large bomb has an explosive diameter of 100 feet. The blast radius of the small bomb is one-fifth the distance of the large bombs diameter. The mid-size bomb has a blast radius that is 20 feet greater than the radius of the small bomb. What is the blast circumference of each of your bombs?” This problem requires the manipulation of both forms of the formula for circumference, $C=2\pi r$ and $C= \pi d$ where r is equal to the radius and d is equal to the diameter. The circumference of the large bomb can be calculated directly from the information provided in the problem. The circumference of the small bomb requires manipulation of the data provided. First, the diameter of the large bomb is divided by five. This determines the blast radius of the small bomb which can be used to determine the circumference. The blast radius of the mid-size bomb is determined by adding 20 feet to the blast radius of the small bomb, and then using this radius in the formula for circumference. The solutions for the circumference are as follows. Large bomb: $100\pi$ or 314.16 feet, Small bomb: $\latex 40\pi$ or 125.66 feet, Mid-size bomb: $60\pi$ or 188.50 feet. I believe that this problem would present an intriguing challenge to the students.

A2: How could you as a teacher create an activity or project that involves your topic?

An engaging activity that involves the determination of circumference will always need to include the manipulation of circles. One creative way to create circles is to form them through bubbles. The title I have chosen for this activity is “Bubblelicious Circumference.” This activity will require the following materials: bubble solution, straws, rulers, paper, and pencil. First the students will clear their desk surface, after which the instructor will pass out the straws, rulers, and pour approximately one tablespoon of bubble solution on the students’ desk. The instructor will also place a small container with bubble solution inside of it on the students’ desk. The students will first dip the end of the straw that will not go into their mouths into the container with bubble solution inside. Next, the students will place the wet end of the straw into the bubble solution on their desk and gently blow air into the bubble solution. The students will continue to blow air until a bubble forms and pops on their desk. Once the bubble pops it will leave a ring of liquid on the surface of their desk in a near perfect circle. The students will then use the ruler to determine the diameter of the circle that is on their desk. This measurement can then be used to determine both the circumference and the radius of the circle. The students will repeat this process at least 10 times, and as many times as the allotted time for the activity will allow. The circumference data will be recorded for each circle formed by each bubble blown on a piece of paper.

Engaging students: The area of a circle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Dale Montgomery. His topic, from Geometry: the area of a circle.

History

Archimedes was the mathematician who we attribute with finding the area of a circle to be Where r is the radius and π is the ratio of circumference to diameter of a circle. (Note that Archimedes was not the first to find the area of a circle, but was the first to find π). I would really like to start the class with something along the lines of introducing Archimedes supposed final words “Do not disturb my circles.” And then go into the death of Archimedes and the mystery surrounding his tomb, such as the account of Cicero and the fact that no one knows where the tomb is now. Cicero said that his tomb had a sphere inscribed in a cylinder, which Archimedes considered to be his greatest mathematical proof. From there, the class should have great interest in what is going on. And we can talk about the fact that the area of a circle is the same as the area a triangle with the same base as the circumference and the same height as the radius.

Rorres, Chris. “Tomb of Archimedes – Illustrations”. Courant Institute of Mathematical Sciences. Retrieved 2011-03-15.

Culture

http://newsfeed.time.com/2013/02/02/are-crop-circles-more-than-just-modern-pranks/

I would show this article in class, most likely passing it out to read. I would ask if they thought it was a prank, and then give them a similar picture as presented in the article but mapped out with radiuses. Then I would say that the average person could do so many square feet of crop’s per hour. If it gets dark at 9 pm and the sun comes up at 6 am, could a person pull a prank like this?

After we discussed how to find the area of a circle I would have found one that it was impossible for one person to do. Then I would display this youtube video.

Seeing that there were 2 people working on it could display that it is possible for it to be a hoax. I like this because it gives the students a way to analyze information that they are given. Does it make sense for these things to be aliens? Not really, so let’s find other explanations. It both introduces the concept and teaches some critical thinking skills.

Applications

You could apply the area of a circle to the diameter of a pizza. When you order pizza you order things like an 8 or a 12 inch. These are diameters and do not give the best idea of how much pizza you are actually getting. You can even include this lesson with a pizza party or something similar. This would easily get kids excited since it is something that most kids like, and they would have the possibility of getting pizza afterwards.

Engaging students: Central and inscribed angles

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Theresa (Tress) Kringen. Her topic, from Geometry: central and inscribed angles.

What interesting word problems using this topic can students do now?

After defining the terms central angle and inscribed angle, students can use a central angles to draw a pie graph or pie chart. They can depict the data using a visual. Based in the percentage of any part of a whole, they will crate a fraction of the whole circle by dividing 360 degrees by that percentage to give the piece of the pie in which they needed to find.

Say a student is given the data below and asked to graph the data into a pie chart:

Students’ favorite colors:

Blue 10

Yellow 3

Red 7

Orange 3

Green 10

Purple 6

Pink 9

Other 2

Students would be required to give percentages based on the 50 students with the percentages listed as: Blue 20%, Yellow 6%, Red 14%, Orange 6%, Green 20%, Purple 12%, Pink 18%, other 4%. This would correspond to the percentage of the 360 degree central angle.

To tie in inscribe angles, I would have to students explain why a pie chart would not work with inscribed angles.

How does this topic appear in high culture?

In order to engage students I could help them understand inscribed angles by relating it to the camera angle in their video games. Describing an inscribed angle as a camera angle on their video game would help them understand it better. As they move throughout the game, their camera angle changes. Based on the camera’s location, you are able to see a certain portion of the screen. If there isn’t much of an angle, the range of view is small or zoomed in. This could be explained as the radius of the circle. The smaller the radius, the less view there is. Thus, the opposite is true. If the radius is large, the camera has a larger view of the object. If the camera has a larger angle of view, more is visible in the camera. I would then relate this to the arc length that the angle creates. I would explain that if the angle of the camera is small, the area of the arc length, or view of the camera would also be small. If the angle of the camera is larger, the arc length or view of the camera is much larger.

How can technology be used to effectively engage students with this topic?

Once students are given the application problem listed above, I could then engage them further by asking them to use word or excel to graph the information given into a document. They would be required to make a chart of the data with the listed percentages of each parameter along with the degree of the angle that the parameter requires to make the pie graph. I would require this since the technology would calculate this on its own without the student having to put in the effort. To make it fun, I would give the students a few extra minutes to make their pie graph their own by customizing it to reflect their personality and style.

To further engage them, I could also ask that each student create a questionnaire that asked each student what their favorite choice of any given set of choices were. They would be required to have at least 7 responses as to make a 7 piece pie chart, but they would be able to choose the topic, and find the information for their parameters on their own. Once they did this, they would be required to make an additional pie chart with their results to present to the class.