Parabolas from String Art (Part 2)

Recently, I announced that my paper Parabolic Properties from Pieces of String had been published in the magazine Math Horizons. The article had multiple aims; in chronological order of when I first started thinking about them:

Prove that string art from two line segments traces a parabola.
Prove that a quadratic polynomial satisfies the focus-directrix property of a parabola, which is the reverse of the usual logic when students learn conic sections.
Prove the reflective property of parabolas.
Accomplish all of the above without using calculus.

While I’m generally pleased with the final form of the article, the necessity of publication constraints somewhat abbreviated the original goal of this project: determining a pedagogically sound way of convincing a bright Algebra I student that string art unexpectedly produces a parabola. While all the necessary mathematics is in the article, I think the article is somewhat lacking on how to sell the idea to students. So, in this series of posts, I’d like to expand on the article with some pedagogical thoughts about connecting string art to parabolas.

As discussed in the previous post, we begin our explorations with string art connecting evenly spaced points on line segments $\overline{AB}$ and $\overline{BC}$ with endpoints $A(0,8)$ , $B(8,0)$ , and $C(16,8)$ . We will call these colored line segments “strings.”

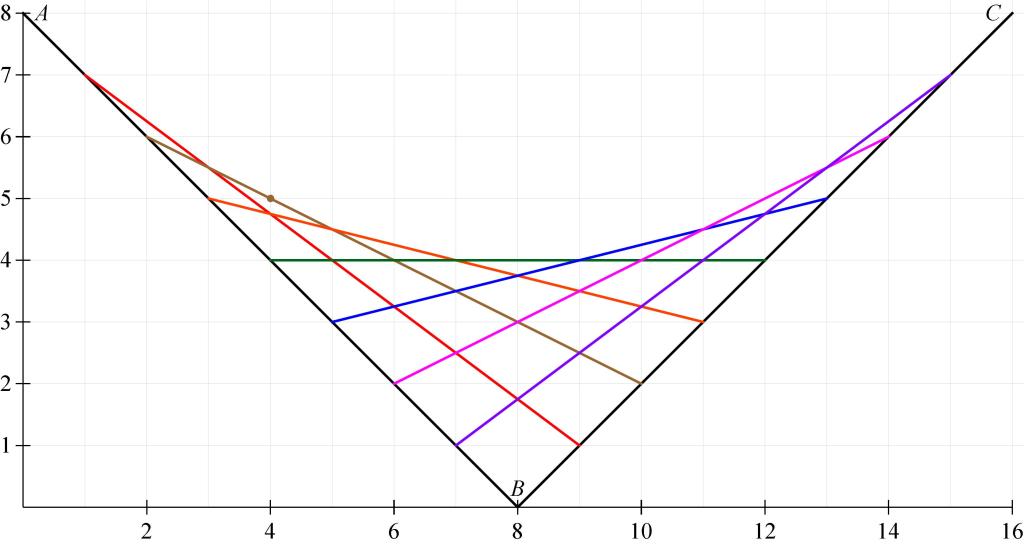
We now ask the following two questions:

For each of $x = 2, 4, 6, 8, 10, 12,$ and $14$ , which string has the largest $y-$ coordinate?
For each of these values of $x$ , what is the value of this largest $y-$ coordinate?

Evidently, for $x=4$ , the brown string that connects $(2,6)$ to $(10,2)$ has the largest $y-$ coordinate. This point is marked with the small brown circle. From the lines on the graph paper, it appears that this brown point is $(4,5)$ .

For $x=8$ , the horizontal green string appears to have the largest $y-$ coordinate, and clearly that point is $(8,4)$ .

For $x=12$ , the pink string that connects $(6,2)$ to $(14,6)$ has the largest $y-$ coordinate. From the lines on the graph paper, it appears that this point is $(12,5)$ .

Unfortunately, for $x=2$ , $x=6$ , $x=10$ , and $x=14$ , it’s evident which string has the largest $y-$ coordinate, but it’s not so easy to confidently read off its value. For this example, this could be solved by using finer graph paper with marks at each quarter (instead of at the integers). However, it’s far better to actually use the point-slope formula to find the equation of the colored line segments.

For example, for $x=2$ , the red string has the largest $y-$ coordinate. This string connects the points $(1,7)$ and $(9,1)$ , and so the slope of this string is $\displaystyle \frac{1-7}{9-1} = -\frac{6}{8} = -0.75$ . Using the point-slope form of a line, the equation of the red string is thus

$y - 7 = -0.75(x - 1)$

$y-7= -0.75x + 0.75$

$y = -0.75x + 7.75$

Substituting $x =2$ , the $y-$ coordinate of the highest string at $x=2$ is $y = -0.75(2) + 7.75 = 6.25$ .

Similarly, at $x=6$ , the equation of the orange string turns out to be $y=-0.25x+5.75$ , and the $y-$ coordinate of the highest string at $x=6$ is $y=-0.25(6)+5.75=4.25$ .

At $x=10$ , the equation of the blue string is $y=0.25x+1.75$ , and the $y-$ coordinate of the highest string at $x=10$ is $y=0.25(10)+1.75=4.25$ .

Finally, at $x=14$ , the equation of the purple string is $y=0.75x-4.25$ , and the $y-$ coordinate of the highest string at $x=14$ is $y=0.75(14)-4.25=6.25$ .

The interested student could confirm the values for $x=4$ , $x=8$ , and $x=12$ that were found earlier by just looking at the picture.

We now add the coordinates of these points to the picture.

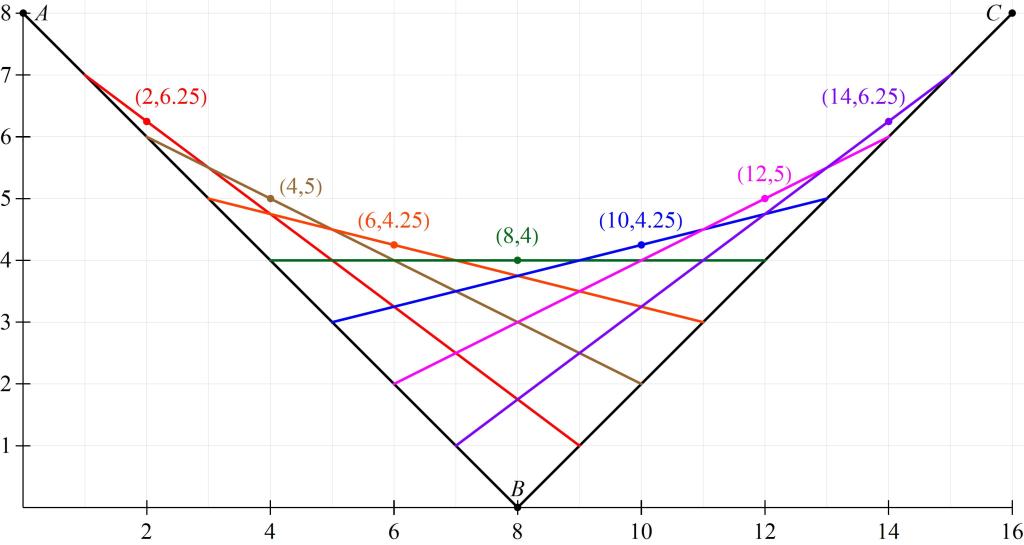
However, perhaps it’s clearer to plot these points on a separate graph, without the clutter of the strings:

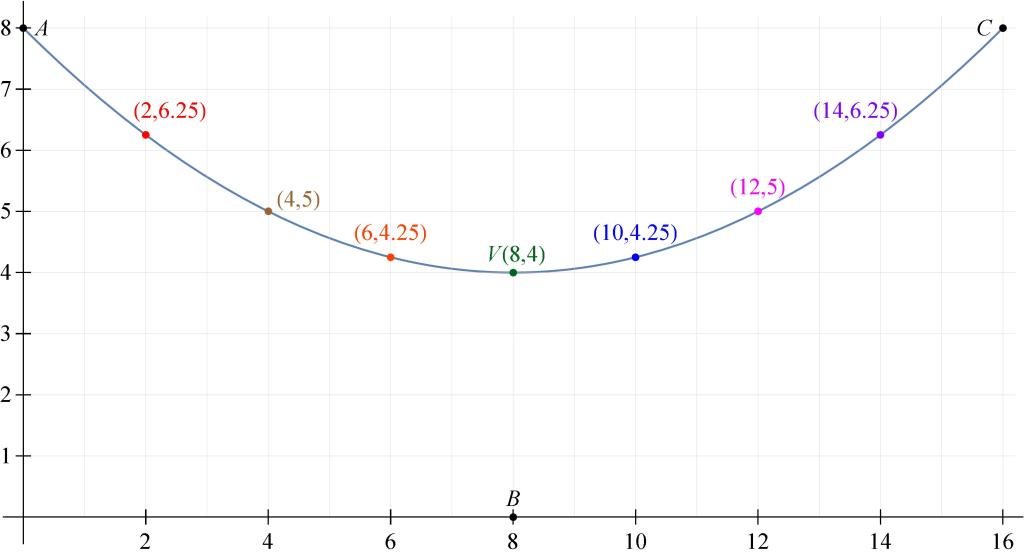
These points are definitely following some kind of curve. In the next post in this series, I’ll discuss a way of convincing students that the curve is actually a parabola.

Parabolas from String Art (Part 1)

Prove that string art from two line segments traces a parabola.
Prove that a quadratic polynomial satisfies the focus-directrix property of a parabola, which is the reverse of the usual logic when students learn conic sections.
Prove the reflective property of parabolas.
Accomplish all of the above without using calculus.

To begin, we use graph paper to sketch to draw coordinate axes, the point $A(0,8)$ , the point $B(8,0)$ , the point $C(16,8)$ , line segment $\overline{AB}$ , and line segment $\overline{BC}$ .

Along $\overline{AB}$ , we mark the evenly spaced points $(1,7)$ , $(2,6)$ , $(3,5)$ , $(4,4)$ , $(5,3)$ , $(6,2)$ , and $(7,1)$ .

Along $\overline{BC}$ , we mark the evenly spaced points $(9,1)$ , $(10,2)$ , $(11,3)$ , $(12,4)$ , $(13,5)$ , $(14,6)$ , and $(15,7)$ .

Next, we draw line segments of different colors to connect:

$(1,7)$ and $(9,1)$
$(2,6)$ and $(10,2)$
$(3,5)$ and $(11,3)$
$(4,4)$ and $(12,4)$
$(5,3)$ and $(13,5)$
$(6,2)$ and $(14,6)$
$(7,1)$ and $(15,7)$

The result should look something like the picture below:

It looks like the string art is tracing a parabola. In this series of posts, I’ll discuss one way that talented algebra students can convince themselves that the curve is indeed a parabola.

Mathematical Imagery: Snow and Sand Patterns

The American Mathematical Society has a neat page of large mathematical images that were created by merely walking in snow and sand. For example, here’s a time-lapse of the 9-hour construction of the Mandelbrot set on a beach (in between high tides and oblivious passers-by that walked through the artwork).

Escher cube in real life

How to Draw with Math

Scientific American had a nice guest article about the intersection of math and art.

The beauty of mathematics – in pictures

From The Guardian: http://www.theguardian.com/science/alexs-adventures-in-numberland/gallery/2014/may/14/beauty-visions-mathematics-pictures?CMP=fb_gu

Art of pi

The picture below is just one of many creative artistic representations of $\pi$ and $e$ found at http://mkweb.bcgsc.ca/pi/

In the words of the author, “Numerology is bogus, but art based on numbers have a beautiful random quality.”

Engaging students: Finding the area of a square or rectangle

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Kayla (Koenig) Lambert. Her topic, from Geometry: finding the area of a square or rectangle.

B) Curriculum: How can this topic be used in student’s future courses in math or science?

Finding the area of a square or rectangle can be applied in many other subjects throughout a student’s school career. This topic is learned around 4^th or 5^th grade, and around this time students will just be using the formulas to find the areas. In middle school, they might be finding the areas by way of more difficult problems, like word problems. The real fun for this subject, in my opinion, doesn’t start until high school. In high school you can use the area of squares and rectangles to find the solutions to many problems. In high school geometry, the Pythagorean Theorem is taught. The area of squares is related to this depending on how the teacher presents this to the student. The Pythagorean Theorem states that “in any right triangle, the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares whose sides are the two legs of the right triangle” (Square-geometry).

In college, possibly high school calculus, students will learn to approximate the total area under a curve (or integral) using the Riemann Sum. To approximate the integral, you find the area of each rectangle, and all of the rectangles areas added together give you the approximated integral. The area of rectangles is also used in Statistics. When creating a histogram, you multiply the height (density) and width of the bars (rectangles). Then adding the areas (relative frequencies) of all of the bars should be equal to one. Students will also need to use the area of squares and rectangles on college placement exams and standardized testing.

C) Culture: How has this topic appeared in high culture (art, classical music, theatre, etc.)?

In my opinion, anything and everything is a form of art, so the area of squares and rectangles can appear in an infinite amount of high culture. M.C. Escher has used squares and rectangles to create tessellations and “portrayed mathematical relationships among shapes, figures and space” (MC Escher). The area of a rectangle was used to Polykeitos the Elder who was a Greek sculptor. He used the area of a rectangle to create the perfect ratio for the human body. Painters also needed to figure out how to depict 3D scenes onto 2D canvas during the Renaissance (Mathematics and Art).

However, one of the more well-known applications of mathematics in art is the Golden Rectangle, which just so happens to involve the area of squares and rectangles. The Golden Rectangle is the area of the original rectangle to the area of the square, which is also the Golden Ratio. In other words, the Golden Rectangle is a rectangle wherein the ratio of its length to its width is the Golden Ratio (Golden Rectangle). Many ancient art and architecture have incorporated the Golden Rectangle into designs. The Golden Rectangle was used in the floor plans and design of the exterior of The Parthenon, which was a Greek temple dedicated to goddess Athena in 5^th century BC (Mathematics and Art). Leonardo DaVinci also used the Golden Rectangle in his work. When painting the Mona Lisa, he used this to “draw attention to the face of the woman in the portrait” (Mathematics and Art). DaVinci also used the Golden Rectangle in the Last Supper using it to create a “perfect harmonic balance between placement of characters in the background” and also used it to arrange the characters around the table (Mathematics and Art).

D) History: Who were some of the people who contributed to the development of this topic?

Finding the area of squares and rectangles didn’t just come out of the blue; we can thank geometry and ancient mathematics for the development of this topic. One person in particular who contributed to the development of this topic was Euclid, or Euclid of Alexandria, who was a Greek mathematician and known as the “Father of Geometry” (Euclid). He was said to revolutionize geometry and his book The Elements is considered the most influential textbook of all time (History of Mathematics). The collection of his books, all thirteen of them, contain all traditional school geometry (Solomon).

However, Euler wasn’t the only one to contribute to this topic. Pythagoras and his students discovered most of what high school students learn in geometry today (History of Mathematics). In the classical period, Aryabhata wrote a treatise including the computation of areas. From the kingdom of Cao Wei, Liu Hui edited and commented on The Nine Chapters of Mathematics Art in 179 AD (History of Mathematics). There are so many people who contributed to this topic, and people are still contributing and developing to the area of squares and rectangles today!

Works Cited

“Euclid – Wikipedia, the free encyclopedia.” Wikipedia, the free encyclopedia. 20 Feb. 2012. http://en.wikipedia.org/wiki/Euclid.

“Golden Rectangle.” Logicville : Puzzles and Brainteasers. 20 Feb. 2012. http://www.logicville.com/sel26.htm.

“M. C. Escher – Wikipedia, the free encyclopedia.” Wikipedia, the free encyclopedia. 20 Feb. 2012. http://en.wikipedia.org/wiki/M._C._Escher.

“Mathematics and art – Wikipedia, the free encyclopedia.” Wikipedia, the free encyclopedia. 20 Feb. 2012. http://www.en.wikipedia.org/wiki/Mathematics_and_art.

Solomon, Robert. The Little Book Of Mathematical Principals, Theories and Things. New York: Metro Books, 2008.

“Square (geometry) – Wikipedia, the free encyclopedia.” Wikipedia, the free encyclopedia. 20 Feb. 2012. http://en.wikipedia.org/wiki/Square_(geometry).

“History of mathematics – Wikipedia, the free encyclopedia.” Wikipedia, the free encyclopedia. 20 Feb. 2012. http://en.wikipedia.org/wiki/History_of_mathematics.