Calculators and complex numbers (Part 9)

In this series of posts, I explore properties of complex numbers that explain some surprising answers to exponential and logarithmic problems using a calculator (see video at the bottom of this post). These posts form the basis for a sequence of lectures given to my future secondary teachers.

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

where $r = |z| = \sqrt{a^2 + b^2}$ and $\tan \theta = b/a$ , with $\theta$ in the appropriate quadrant. As noted before, this is analogous to converting from rectangular coordinates to polar coordinates.

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

In the previous three posts, we discussed De Moivre’s Theorem:

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

Yesterday, we used factoring to show that there are three solutions to $z^3 = -27$ , namely, $z = -3$ and $z = \displaystyle \frac{3}{2} \pm \frac{3\sqrt{3}}{2} i$ . Let’s now use De Moivre’s Theorem to take on the same task. As we’ll see, De Moivre’s Theorem provides a geometrical interpretation of this result that isn’t readily apparent using solely algebra.

Let $z = r(\cos \theta + i \sin \theta)$ , so that

$z^3 = -27$

becomes

$r^3 (\cos 3\theta + i \sin 3 \theta) = 27 (\cos \pi + i \sin \pi)$

We now match the corresponding parts. The distances from the original have to match, so that $r^3 = 27$ , or $r = 3$ . (Notice that there is only one answer because $r$ must be a positive real number.) Also, the angles $3\theta$ and $\pi$ must be coterminal. They do not necessarily have to be equal, but the angles must point in the same direction. Therefore,

$3 \theta = \pi + 2\pi k$ , or $\theta = \displaystyle ]frac{\pi}{3} + \frac{2\pi k}{3}$

for any integer $k$ . At first blush, it appears that there are infinitely many solutions $z$ since there are infinitely many possible angles $\theta$ . However, it turns out that there are only three answers, as expected.

Let’s now plug in numbers for $k$ . Let’s use the easiest three numbers, $k = 0, 1, 2$ .

If $k = 0$ , then $\theta = \displaystyle \frac{\pi}{3}$ , so that

$z = 3 \displaystyle \left( \cos \frac{\pi}{3} + i \sin \frac{\pi}{3} \right)$

$= 3 \displaystyle \left( \frac{1}{2} + i \frac{\sqrt{3}}{2} \right)$

$= \displaystyle \frac{3}{2} + \frac{3\sqrt{3}}{2} i$ .

If $k = 1$ , then $\theta = \displaystyle \frac{\pi}{3} + \frac{2\pi}{3} = \pi$ , so that

$z = 3 \displaystyle \left( \cos \pi + i \sin \pi \right) = 3(-1+0i) = -3$ .

If $k = 2$ , then $\theta = \displaystyle \frac{\pi}{3} + \frac{4\pi}{3} = \displaystyle \frac{5\pi}{3}$ , so that

$z = 3 \displaystyle \left( \cos \frac{5\pi}{3} + i \sin \frac{5\pi}{3} \right)$

$= 3 \displaystyle \left( \frac{1}{2} - i \frac{\sqrt{3}}{2} \right)$

$= \displaystyle \frac{3}{2} - \frac{3\sqrt{3}}{2} i$ .

Not surprisingly, we obtain the same three answers that we did using algebra.

What if we keep increasing the value of $k$ ? Let’s find out with $k = 3$ :

If $k = 3$ , then $\theta = \displaystyle \frac{\pi}{3} + \frac{6\pi}{3} = \displaystyle \frac{7\pi}{3}$ , so that

$z = 3 \displaystyle \left( \cos \frac{7\pi}{3} + i \sin \frac{7 \pi}{3} \right)$

$= 3 \displaystyle \left( \frac{1}{2} + i \frac{\sqrt{3}}{2} \right)$

$= \displaystyle \frac{3}{2} + \frac{3\sqrt{3}}{2} i$ .

In other words, since $\displaystyle \frac{\pi}{3}$ and $\displaystyle \frac{7\pi}{3}$ are coterminal, we end up with the same answer. This resolves the apparent paradox of having infinitely many possible angles $\theta$ but only three solutions $z$ .

Using De Moivre’s Theorem certainly appears to be much more difficult than just factoring! However, this solution provides a geometric interpretation of the three roots that isn’t otherwise apparent. Let’s using the trigonometric form of these three solutions to plot them in the complex plane:

complex roots –

All three points lie a distance of 3 from the origin, and so they lie on the same circle. Also, the angle from the origin increases by $\displaystyle \frac{2\pi}{3}$ as we shift from point to point. This divides the circle (with a total angle of $2\pi$ into three equal parts, and so the points are evenly spaced around the circle. Also, the points form the vertices of an equilateral triangle inscribed within this circle. Again, none of this would have been apparent by strictly factoring the polynomial $z^3 + 27$ .

All of the above can be repeated for finding the roots of any equation $z^n = w$ . This equation has $n$ roots which lie a distance of $|w|^{1/n}$ from the origin on the points of a regular $n-$ gon inscribed in a circle of this radius. The only tricky part is determining the placement of the initial point (i.e., finding the initial value of $\theta$ from which all other points can be determined.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 8)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

In the previous three posts, we discussed De Moivre’s Theorem:

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

Let’s now use this theorem to solve an algebraic equation.

Find all $z$ so that $z^3 = -27$ .

When I present this to my students, their kneejerk reaction is always to answer “ $-3$ .” To which I politely point out, “This is a cubic equation. So how many roots does it have?” Of course, they answer “Three.” To which I respond, “OK, so how do we find the other two roots?”

With enough patience, a student will usually volunteer that $z^3 + 27 = 0$ has a known root of $z = -3$ , and so the remaining roots can be found using synthetic division by dividing $z+3$ into $z^3 + 27$ , yielding

$z^3 + 27 = (z+3)(z^2 - 3z + 9)$

So the other two roots can be found using the quadratic formula:

$z = \displaystyle \frac{3 \pm \sqrt{9 - 36}}{2} = \displaystyle \frac{3}{2} \pm \frac{3\sqrt{3}}{2} i$

So there are indeed three roots. Though I usually won’t take class time to do it, I encourage my students to cube these two answers to confirm that they indeed get $-27$ .

As an aside, before moving on to the use of De Moivre’s Theorem, I usually point out to my students that there is a formula for factoring the sum of two cubes:

$a^3 + b^3 = (a+b)(a^2 - ab + b^2)$

And there’s a formula for the difference of two cubes:

$a^3 - b^3 = (a-b)(a^2 + ab + b^2)$

My experience is that even math majors are not familiar with these two formulas. They know the difference of two squares formula, but they’re either not proficient with these two formulas or else they’ve never seen them before. These can be generalized for any odd positive exponent and any positive exponent, respectively.

In tomorrow’s post, I’ll describe how these three roots can be found by using De Moivre’s Theorem.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 7)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

This post builds off the previous two posts by completing the proof of De Moivre’s Theorem.

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

The proof has two parts:

For $n \ge 0$ : proof by induction.
For $n < 0$ : let $n = -m$ , and then use part 1.

In the previous post, I presented how I describe the proof of step 1 to students. Today, I’ll discuss how I present step 2.

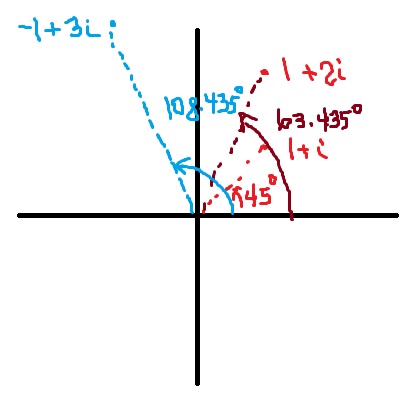
My personal opinion is that the proof of step 2 goes easiest when a numerical example is done first. Let $n = -5$ . Students can usually volunteer the successive steps of this special case:

$\left[ r (\cos \theta + i \sin \theta) \right]^{-5} = \displaystyle \frac{1}{ \left[ r (\cos \theta + i \sin \theta) \right]^{5} }$

$= \displaystyle \frac{1}{r^5 (\cos 5 \theta + i \sin 5 \theta)}$

At this point, students usually want to multiply by the conjugate of the denominator. There’s nothing wrong with doing that, of course, but it’s more elegant to write the numerator in trigonometric form:

$= \displaystyle \frac{1(\cos 0 + i \sin 0)}{r^5 (\cos 5 \theta + i \sin 5 \theta)}$

$= r^{-5} (\cos [0-5\theta] + i \sin[0-5\theta] )$

$= r^{-5} (\cos [-5\theta] + i \sin[ - 5\theta])$ ,

which matches what we would have expected. Students are now prepared for the proof, which I try to place alongside the above computation for $n = -5$ .

Proof for $n < 0$ . Let $n = -m$ . I tell students to imagine that $n$ is $-5$ , so that $m$ is equal to (students volunteer) $5$ . In other words, $n$ is negative and $m$ is positive. Then

$\left[ r (\cos \theta + i \sin \theta) \right]^{n} = \displaystyle \frac{1}{ \left[ r (\cos \theta + i \sin \theta) \right]^{-n} }$

I again remind everyone that $-n = m$ is positive, and so (like a good MIT freshman) the previous work applies:

$= \displaystyle \frac{1}{ \left[ r (\cos \theta + i \sin \theta) \right]^m }$

The remaining steps mirror the calculation above:

$= \displaystyle \frac{1}{r^m (\cos m \theta + i \sin m \theta)}$

$= \displaystyle \frac{1(\cos 0 + i \sin 0)}{r^m (\cos m \theta + i \sin m \theta)}$

$= r^{-m} (\cos [0-m\theta] + i \sin[0-m\theta] )$

$= r^{-m} (\cos [-m\theta] + i \sin[ - m \theta])$

$= r^{n} (\cos [n\theta] + i \sin[ n \theta])$ ,

thus ending the proof. green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 6)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

In the previous post, I used a numerical example to justify De Moivre’s Theorem:

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

The proof has two parts:

For $n \ge 0$ : proof by induction.
For $n < 0$ : let $n = -m$ , and then use part 1.

In this post, I describe how I present part 1 to students in class. The next post will cover part 2. As noted before, I typically present this theorem and its proof after a numerical example so that students can guess the statement of the theorem on their own.

Proof for $n \ge 0$ .

Base Case: $n = 0$ . This is trivial, as the left-hand side is

$\left[ r (\cos \theta + i \sin \theta) \right]^0 = 1$ ,

while the right-hand side is

$r^0 (\cos 0 \theta + i \sin 0 \theta) = 1(\cos 0 + i \sin 0) = 1(1 + 0i) = 1$ .

Assumption. We now assume, for a given integer $latex $n$, that

$\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

Inductive Step. We now use the above assumption to prove the statement for $n+1$ . On the board, I write the left-hand side on the top and the right-hand side on the bottom, leaving plenty of space in between:

$\left[ r (\cos \theta + i \sin \theta) \right]^{n+1}$

$\quad$

$= r^{n+1} (\cos [n+1] \theta + i \sin [n+1] \theta)$ .

All we have to do is fill in the space to transform the left-hand side into the target on the right-hand side. (I like to call the right-hand side “the target,” as it suggests the direction in which the proof should aim.) I also tell the class that we’re more than two-thirds done with the proof, since we’ve finished the first two steps and have made some headway on the third. This usually produces knowing laughter since the hardest part of the proof is creatively converting the left-hand side into the target.

The first couple steps of the proof are usually clear to students:

$\left[ r (\cos \theta + i \sin \theta) \right]^{n+1} = \left[ r (\cos \theta + i \sin \theta) \right]^n \cdot \left[ r (\cos \theta + i \sin \theta) \right]$

$= \left[ r^n (\cos n \theta + i \sin n \theta) \right] \cdot \left[ r (\cos \theta + i \sin \theta) \right]$

by induction hypothesis. (I’ll also remind students that, as a general rule, when doing a proof by induction, it’s important to actually use the inductive assumption someplace.) At this point, most students want to distribute to get the right answer. This will eventually produce the correct answer using trig identities. However, I again try to encourage them to think like MIT freshmen and use previous work. After all, the distances multiply and the angles add, so the next step can be

$=r^n \cdot r (\cos [n \theta + \theta] + i \sin [n \theta + \theta])$

$= r^{n+1} (\cos [n+1]\theta + i \sin [n+1]\theta)$ .

In tomorrow’s post, I’ll talk about how I present the second part of the proof to my students.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 5)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

The trigonometric form of a complex number permits a geometric interpretation of multiplication, given in the following theorem.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

While this theorem doesn’t seem all that helpful — just multiplying complex numbers seems easier — this theorem will be a great help for the following problem:

Compute $(\sqrt{3} + i)^{2014}$ . (When teaching this in class, I usually choose the exponent to be the current year.)

Let’s discuss the options for evaluating this expression.

Method #1: Multiply it out. (Students reflexively wince in pain — or knowing laughter — when I make this suggestion.)

Method #2: Use the 2014th row of Pascal’s triangle. (More pain and/or laughter.)

Method #3: Use the above theorem. It’s straightforward to write $\sqrt{3} + i$ as $2 \displaystyle \left( \cos \frac{\pi}{6} + i \sin \frac{\pi}{6} \right)$ … for reasons that will become apparent later, I tell my students that I’ll use radians and not degrees for this one. Most students can recognize — and this is important, before I formally prove De Moivre’s Theorem — that they need to multiply $2$ by itself 2014 times and add $\displaystyle \frac{\pi}{6}$ to itself 2014 times. Therefore,

$(\sqrt{3} + i)^{2014} = \displaystyle 2^{2014} \left( \cos \frac{2014\pi}{6} + i \sin \frac{2014\pi}{6} \right) = \displaystyle 2^{2014} \left( \cos \frac{1007\pi}{3} + i \sin \frac{1007\pi}{3} \right)$

I then try to coax my students to compute $\displaystyle \cos \frac{1007\pi}{3}$ without a calculator. With some prodding, they’ll recognize that $\displaystyle \frac{1007}{3} = \displaystyle {335}\frac{2}{3}$ , and so they can subtract $334\pi$ (not $335\pi$ ) without changing the values of sine and cosine. Therefore,

$(\sqrt{3} + i)^{2014} = \displaystyle 2^{2014} \left( \cos \frac{5\pi}{3} + i \sin \frac{5\pi}{3} \right)$

$= 2^{2014} \left( \frac{1}{2} - i \frac{\sqrt{3}}{2} \right)$

$= 2^{2013} (1-i\sqrt{3})$

By this point, students absolutely believe that the trigonometric form of a complex number serves a useful purpose. Also, this numerical example has prepared students for the formal proof of DeMoivre’s Theorem, which will be the subject of the next two posts.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 4)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

In the previous post, I proved the following theorem which provides a geometric interpretation for multiplying complex numbers.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

Perhaps unsurprisingly, there’s also a theorem for dividing complex numbers. Students can using guess the statement of this theorem.

Theorem. $\displaystyle \frac{ r_1 (\cos \theta_1 + i \sin \theta_1) }{ r_2 (\cos \theta_2 + i \sin \theta_2) } = \displaystyle \frac{r_1}{r_2} (\cos [\theta_1-\theta_2] + i \sin [\theta_1-\theta_2])$ .

Proof. The proof begins by separating the $r_1$ and $r_2$ terms and then multiplying by the conjugate of the denominator:

$\displaystyle \frac{ r_1 (\cos \theta_1 + i \sin \theta_1) }{ r_2 (\cos \theta_2 + i \sin \theta_2) }$

$= \displaystyle \frac{r_1}{r_2} \cdot \frac{ \cos \theta_1 + i \sin \theta_1 }{ \cos \theta_2 + i \sin \theta_2 } \cdot \frac{ \cos \theta_2 - i \sin \theta_2 }{ \cos \theta_2 - i \sin \theta_2 }$

$= \displaystyle \frac{r_1}{r_2} \cdot \frac{ (\cos \theta_1 + i \sin \theta_1)( \cos \theta_2 - i \sin \theta_2) } {\cos^2 \theta_2 - i^2 \sin^2 \theta_2}$

$= \displaystyle \frac{r_1}{r_2} \cdot \frac{ (\cos \theta_1 + i \sin \theta_1)( \cos \theta_2 - i \sin \theta_2) } {\cos^2 \theta_2 + \sin^2 \theta_2}$

$= \displaystyle \frac{r_1}{r_2} (\cos \theta_1 + i \sin \theta_1)( \cos \theta_2 - i \sin \theta_2)$

At this juncture in the proof, there are two legitimate ways to proceed.

Method #1: Multiply out the right-hand side. After all, this is how we proved the theorem yesterday. For this reason, students naturally gravitate toward this proof, and the proof works after recognizing the trig identities for the sine and cosine of the difference of two angles.

However, this isn’t the most elegant proof.

Method #2: I break out my old joke about the entrance exam at MIT and the importance of using previous work. I rewrite the right-hand side as

$= \displaystyle \frac{r_1}{r_2} (\cos \theta_1 + i \sin \theta_1)( \cos [-\theta_2] + i \sin [-\theta_2])$ ;

this also serves as a reminder about the odd/even identities for sine and cosine, respectively. Then students observe that the right-hand side is just a product of two complex numbers in trigonometric form, and so the angle of the product is found by adding the angles.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 3)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

Why is this important? When students first learn to multiply complex numbers like $1+i$ and $2+i$ , they are taught to just distribute (or, using the nomenclature that I don’t like, FOIL it out):

$(1+i)(1+2i) = 1 + 2i + i + 2i^2 = 1 + 3i - 2 = -1 + 3i$ .

The trigonometric form of a complex number permits a geometric interpretation of multiplication, given in the following theorem.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

Proof. As above, we distribute (except for the $r_1$ and $r_2$ terms):

$\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right]$

$= r_1 r_2 (\cos \theta_1 \cos \theta_2 + i \cos \theta_1 \sin \theta_2 + i \sin \theta_1 \cos \theta_2 + i^2 \sin \theta_1 \sin \theta_2$

$= r_1 r_2 (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 + i[ \sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2])$

$= r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

When actually doing this in class, the big conceptual jump for students is the last step. So I make a big song-and-dance routine out of this:

Cosine of the first times cosine of the second minus sine of the first times sine of the second… where have I seen this before?

The idea is for my students to search deep into their mathematical memories until they recall the appropriate trig identity.

For the original multiplication problem, we see that

$1+i = \sqrt{2} \left( \cos 45^\circ + i \sin 45^\circ \right)$

$1 + 2i = \sqrt{5} \left( \cos[\tan^{-1} 2] + i \sin[\tan^{-1} 2] \right) \approx \sqrt{5} \left( \cos 63.435^\circ + i \sin 63.435^\circ \right)$

Therefore, the product of $1+i$ and $1+2i$ will be a distance of $\sqrt{2} \cdot \sqrt{5} = \sqrt{10}$ from the origin, and the angle from the positive real axis will be $45^\circ + \tan^{-1} 2 \approx 45^\circ + 63.435^\circ = 108.435^\circ$ . Indeed,

$-1 + 3i \approx \sqrt{10} \left( \cos 108.435^\circ + i \sin 108.435^\circ \right)$ .

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Formal logic bumper sticker

Source: http://www.xkcd.com/1033/

A New Proof of the Law of Cosines

Source: https://www.facebook.com/AmerMathMonthly/photos/a.250425975006394.53155.241224542593204/635754956473492/?type=1&theater

Engaging students: the difference of two squares

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Dale Montgomery. His topic, from Algebra II: the difference of two squares.

Application/Future Curriculum (science)-

You can use difference of squares to find a basic formula to be used in any problem where you drop an object and want to find what time it will take to land. This physics concept will be of interest to your students considering any mechanical science and a useful tool to introduce problem solving by manipulating equations.

Take any height $h$ . If you were to drop an object from this height then it could be modeled with a distance over time graph using the equation

$(h- 9.8/2) t^2$ .

By applying difference of squares you get the expression

$[\sqrt{h}+\sqrt{4.9}] t) \times ( [\sqrt{h} - \sqrt{4.9}] t)$ .

Then by setting this expression equal to 0 and manipulating you would get that
$t = \pm \displaystyle \frac{\sqrt{h}}{\sqrt{4.9}}$ .

I like a situation like this because it allows you to give them linking knowledge about quadratic equations. Most students may not have been exposed to this type of physics yet. However, it is a requirement, and having this knowledge will help them in that class. On top of that it helps with equation manipulation and answering the question, “Does my answer make sense.” This question needs to be asked since it is possible for a student to get an answer of negative time. All of these skills combined with the new topic of difference of squares make for a multifaceted problem. This would probably not be great for day 1 of difference of squares, but I could see it as an engage for the continuance of the lesson.

Curriculum:

You can use the idea of graphing to show that difference of squares works. This is a good way to give visual representation to your students who need it. If you compare the factoring of $x^2-9$ to the graph of $y=x^2-9$ and finding the roots of that graph, you can show that they have the same solutions. It is not that novel, but this visual can just help the idea click into students’ minds.

Manipulative

A manipulative that I got the idea for from http://www.gbbservices.com/math/squarediff.html is using squares to show the difference of squares. This is done quite easily as shown in the picture below. This could be done along a lesson on difference of squares. Maybe this would follow easily from a factoring using algebra tiles. The image below is fairly self explanatory and would really help if made into a hands-on manipulative that kinesthetic learners could make great use of.