In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.
This story, that I’ll share with my Precalculus students, comes from Fall 1996, my first semester as a college professor. I was teaching a Precalculus class, and the topic was vectors. I forget the exact problem (believe me, I wish I could remember it), but I was going over the solution of a problem that required finding  . I told the class that I had worked this out ahead of time, and that the approximate answer was
. I told the class that I had worked this out ahead of time, and that the approximate answer was  . Then I used that angle for whatever I needed it for and continued until obtaining the eventual solution.
. Then I used that angle for whatever I needed it for and continued until obtaining the eventual solution.
(By the way, I now realize that I was hardly following best practices by computing that angle ahead of time. Knowing what I know now, I should have brought a calculator to class and computed it on the spot. But, as a young professor, I was primarily concerned with getting the answer right, and I was petrified of making a mistake that my students could repeat.)
After solving the problem, I paused to ask for questions. One student asked a good question, and then another.
Then a third student asked, “How did you know that  was
was  ?
?
Suppressing a smile, I answered, “Easy; I had that one memorized.”
The class immediately erupted… some with laughter, some with disbelief. (I had a terrific rapport with those students that semester; part of the daily atmosphere was the give-and-take with any number of exuberant students.) One guy in the front row immediately challenged me: “Oh yeah? Then what’s 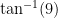 ?
?
I started to stammer, “Uh, um…”
“Aha!” they said. “He’s faking it.” They start pulling out their calculators.
Then I thought as fast as I could. Then I realized that I knew that  , thanks to my calculation prior to class. I also knew that
, thanks to my calculation prior to class. I also knew that 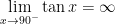 since the graph of
since the graph of  has a vertical asymptote at
has a vertical asymptote at  . So the solution to
. So the solution to 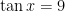 had to be somewhere between
had to be somewhere between  and
and 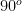 .
.
So I took a total guess. “ ,” I said, faking complete and utter confidence.
,” I said, faking complete and utter confidence.
Wouldn’t you know it, I was right. (The answer is about  .)
.)
In stunned disbelief, the guy who asked the question asked, “How did you do that?”
I was reeling in shock that I guessed correctly. But I put on my best poker face and answered, “I told you, I had it memorized.” And then I continued with the next example. For the rest of the semester, my students really thought I had it memorized.
To this day, this is my favorite stunt that I ever pulled off in front of my students.
definition of a limit is often really hard for students to swallow:
, or
they give me, I can find an
that meets the requirements of this limit.


