Solving Problems Submitted to MAA Journals (Part 6a)

The following problem appeared in Volume 97, Issue 3 (2024) of Mathematics Magazine.

Two points $P$ and $Q$ are chosen at random (uniformly) from the interior of a unit circle. What is the probability that the circle whose diameter is segment $\overline{PQ}$ lies entirely in the interior of the unit circle?

It took me a while to wrap my head around the statement of the problem. In the figure, the points $P$ and $Q$ are chosen from inside the unit circle (blue). Then the circle (pink) with diameter $\overline{PQ}$ has center $M$ , the midpoint of $\overline{PQ}$ . Also, the radius of the pink circle is $MP=MQ$ .

The pink circle will lie entirely the blue circle exactly when the green line containing the origin $O$ , the point $M$ , and a radius of the pink circle lies within the blue circle. Said another way, the condition is that the distance $MO$ plus the radius of the pink circle is less than 1, or

$MO + MP < 1$ .

As a first step toward wrapping my head around this problem, I programmed a simple simulation in Mathematica to count the number of times that $MO + MP < 1$ when points $P$ and $Q$ were chosen at random from the unit circle.

In the above simulation, out of about 61,000,000 attempts, 66.6644% of the attempts were successful. This leads to the natural guess that the true probability is $2/3$ . Indeed, the 95% confidence confidence interval $(0.666524, 0.666764)$ contains $2/3$ , so that the difference of $0.666644$ from $2/3$ can be plausibly attributed to chance.

I end with a quick programming note. This certainly isn’t the ideal way to perform the simulation. First, for a fast simulation, I should have programmed in C++ or Python instead of Mathematica. Second, the coordinates of $P$ and $Q$ are chosen from the unit square, so it’s quite possible for $P$ or $Q$ or both to lie outside the unit circle. Indeed, the chance that both $P$ and $Q$ lie in the unit disk in this simulation is $(\pi/4)^2 \approx 0.617$ , meaning that about $38.3\%$ of the simulations were simply wasted. So the only sense that this was a quick simulation was that I could type it quickly in Mathematica and then let the computer churn out a result. (I’ll talk about a better way to perform the simulation in the next post.)

How to Detect a Change in the Slope of Your Data

Source: https://xkcd.com/2701/

Selection Bias

Engaging students: Defining a function of one variable

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Lydia Rios. Her topic, from Algebra: defining a function of one variable.

How does this topic extend what your students should have learned in previous courses?

From Prekindergarten and up, students have been practicing skills that prepared them from the concepts of a function. By counting they knew that they were adding that same number to every other number in the same sequence. By doing 1,2,3,4,5,… counting by ones they realized that every left number was being added by one to get the right number. They were taking the input 2 and doing the operation of addition by 1 to get the output of 3. The same thing was happening for other counting sequences, or even general operation statements such as 1+7=8. They have been building up to the idea of functions without recognizing that they were. You can use this no simple idea that’s been installed in them to understand what functions are. You can build them up from here and then start giving them statements with a missing component so they can find a missing variable. Then finally, building them towards defining a function where you give them similar statements with a missing component so that they can start writing out their own equations. *Don’t forget to introduce input and output and that are function represent the relationship between out input (x) is having this operation done to it to get our output (y).

Mathematics Vertical Alignment, Prekindergarten-Grade 2 (texas.gov)

Introduction to Functions | Boundless Algebra (lumenlearning.com)

How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?

You could use different appearances in pop culture to get students to understand input and output, such as when you are playing video games you are putting your input on the controller to get the output on the screen. However, this may not have an association with function unless you want to start getting into detail about programming. Therefore, to bring about the topic of functions I would just use a word problem that associates with pop culture. You could also bring the business side of pop culture into the class, such as setting up an equation that shows how the more tickets bought makes and increased revenue for the production of a movie. For example, lets say a ticket cost $8.50 and the production get’s 40% of the profit. Then you could set up the equal as 0.40(8.5X)=Y with 0.40 representing 40% of the profit that the production team will receive of the $8.50 tickets.

How has this topic appeared in high culture (art, classical music, theatre, etc.)?

The topic of inputs and outputs can be touched on in reference to theatre. Both in lighting and sound, inputs and outputs are used. Therefore, the concept of this can be taught to the students. For lighting, you can talk about DMX which is what LED lights use so that the technology in the lights can pick up the functions that the computer is telling it to do. You connect the DMX in cord to the DMX in into the lighting board and then the DMX out of the lighting board to the DMX out on the lights. The same idea works with audio. However, the inputs are the microphones and the outputs are the speakers. You would take the microphone aux cord and plug that into the inputs on the Sound Board and then you would take the speaker cord and plug that into the outputs on the Sound Board. Therefore, that particular microphone is connected to that speaker and will only come out of that speaker.

“Welcome to Coolmath.” Cool Math – Free Online Cool Math Lessons, Cool Math Games & Apps, Fun Math Activities, Pre-Algebra, Algebra, Precalculus, www.coolmath.com/algebra/15-functions.

Constructing the Null and Alternate Hypotheses

Thoughts on Numerical Integration (Part 23): The normalcdf function on TI calculators

I end this series about numerical integration by returning to the most common (if hidden) application of numerical integration in the secondary mathematics curriculum: finding the area under the normal curve. This is a critically important tool for problems in both probability and statistics; however, the antiderivative of $\displaystyle \frac{1}{\sqrt{2\pi}} e^{-x^2/2}$ cannot be expressed using finitely many elementary functions. Therefore, we must resort to numerical methods instead.

In days of old, of course, students relied on tables in the back of the textbook to find areas under the bell curve, and I suppose that such tables are still being printed. For students with access to modern scientific calculators, of course, there’s no need for tables because this is a built-in function on many calculators. For the line of TI calculators, the command is normalcdf.

Unfortunately, it’s a sad (but not well-known) fact of life that the TI-83 and TI-84 calculators are not terribly accurate at computing these areas. For example:

TI-84: $\displaystyle \int_0^1 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx \approx 0.3413447\underline{399}$

Correct answer, with Mathematica: $0.3413447\underline{467}\dots$

TI-84: $\displaystyle \int_1^2 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx \approx 0.1359051\underline{975}$

Correct answer, with Mathematica: $0.1359051\underline{219}\dots$

TI-84: $\displaystyle \int_2^3 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx \approx 0.021400\underline{0948}$

Correct answer, with Mathematica: $0.021400\underline{2339}\dots$

TI-84: $\displaystyle \int_3^4 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx \approx 0.0013182\underline{812}$

Correct answer, with Mathematica: $0.0013182\underline{267}\dots$

TI-84: $\displaystyle \int_4^5 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx \approx 0.0000313\underline{9892959}$

Correct answer, with Mathematica: $0.0000313\underline{84590261}\dots$

TI-84: $\displaystyle \int_5^6 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx \approx 2.8\underline{61148776} \times 10^{-7}$

Correct answer, with Mathematica: $2.8\underline{56649842}\dots \times 10^{-7}$

I don’t presume to know the proprietary algorithm used to implement normalcdf on TI-83 and TI-84 calculators. My honest if brutal assessment is that it’s probably not worth knowing: in the best case (when the endpoints are close to 0), the calculator provides an answer that is accurate to only 7 significant digits while presenting the illusion of a higher degree of accuracy. I can say that Simpson’s Rule with only $n = 26$ subintervals provides a better approximation to $\displaystyle \int_0^1 \frac{e^{-x^2/2}}{\sqrt{2\pi}} \, dx$ than the normalcdf function.

For what it’s worth, I also looked at the accuracy of the NORMSDIST function in Microsoft Excel. This is much better, almost always producing answers that are accurate to 11 or 12 significant digits, which is all that can be realistically expected in floating-point double-precision arithmetic (in which numbers are usually stored accurate to 13 significant digits prior to any computations).

Engaging students: Making and interpreting bar charts, frequency charts, pie charts, and histograms

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Taylor Bigelow. Her topic, from Pre-Algebra: making and interpreting bar charts, frequency charts, pie charts, and histograms.

How could you as a teacher create an activity or project that involves your topic?

Charts allow for a lot of fun class activities. For example, we can have them take their own data for a table and create charts from that data. For my activity, I will give them all dice, which they should be very familiar with, and have them roll the dice 20 times and keep track of how many times it lands on each number in a table. From that table, they will make their own bar charts, frequency charts, and pie charts. After they roll their dice and make their charts, they will then answer questions interpreting the charts. This tests their ability to understand data and make all the different types of charts.

How has this topic appeared in the news?

Charts are all over in the news, especially recently. There were pie charts and frequency charts all over during the election cycle, and with covid, all we see is bar charts of covid data. An easy engage for this topic would be to make observations about these types of graphs that they’ll probably see all the time during election seasons and might even be familiar with. First, we will ask the students what news can benefit from graphs, and what news they have seen graphs in recently. I expect answers similar to elections, covid, and economics. Then we can look at some of the graphs that usually show up around election cycles. We will take a minute as a class to discuss what they notice about the graphs and what they mean. Questions like “what type of graph is this”, “what are the variables in this graph”, and “what information do you get from this graph”. 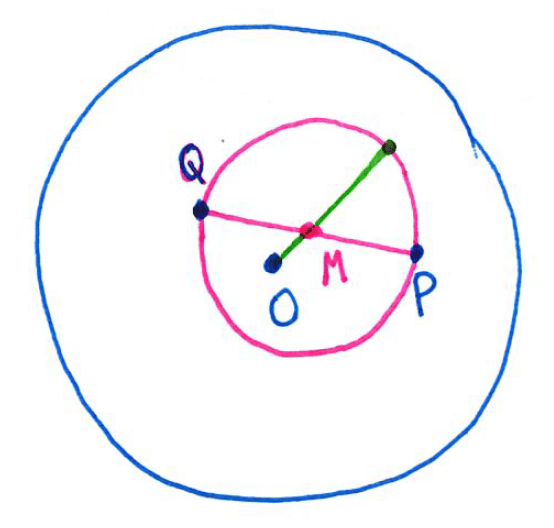This will show the students that being able to read these graphs has real life applications, and it also teaches them what important things to look for in the graphs during class time and homework.

How can technology be used to effectively engage students with this topic?

Technology is very useful for making graphs and being able to make and manipulate graphs can help them understand how to interpret the information given in graphs. Google sheets or excel can both be used to make and manipulate graphs. For this activity we would give the students some sample data and have them enter it into an online spreadsheet, and then make an appropriate graph to show this data. They then would answer questions about this graph, like “Why did you choose this type of graph to represent the data?”, “what is the independent variable and what is the dependent variable”, “What observations can you make about this graph?”, and “What would happen if you changed X to be # instead? Or if you added more information?” and other questions, especially about graphs with multiple variables. This helps students see how different information can be represented and lets them experiment with the information on their own, while also answering questions that steer them in the direction that the teacher wants them to know.