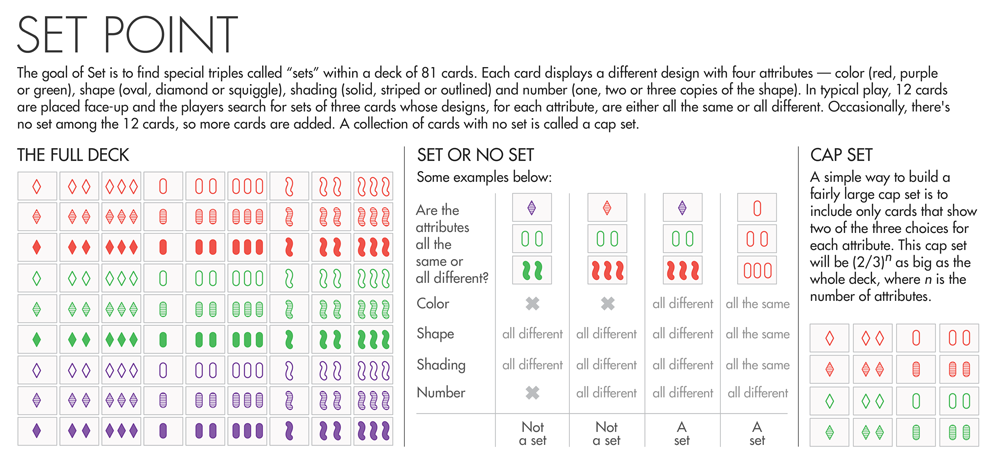
From http://devlinsangle.blogspot.com/2016/03/the-math-myth-that-permeates-math-myth.html:
March 1 saw the publication of the book The Math Myth: And Other STEM Delusions, by Andrew Hacker. MAA members are likely to recognize the author’s name from an opinion piece he published in the New York Times in 2012, with the arresting headline “Is Algebra Necessary?”
…
On page 48, Hacker presents a question he took from an MCAT paper. It provides some technical data and asks what happens to the ratio of two inverse-square law forces between charges of given masses when the distance between them is halved. The context Hacker provides for this question is that medical professionals needs to be able to read and understand the mathematics used in technical papers. His claim is that this requirement does not extend to the physics of electrical and gravitational forces. In that, he is surely correct… What this question is asking for is, Do you understand what a ratio is? Surely that is something that any medical professional who will have to read and understand journal articles would need to know. Hacker completely misses this simple observation, and presents the question as an example of baroque mathematical testing run amok.
On page 70, he presents a question from an admissions test for selective high schools. A player throws two dice and the same number comes up on both. The question asks the student to choose the probability that the two dice sum to 9 from the list 0, 1/6, 2/9, 1/2, 1/3. Hacker’s problem is that the student is supposed to answer this in 90 seconds. Now, I share Hacker’s disdain for time-limited questions, but in this case the answer can only be 0. It’s not a probability question at all, and no computation is required. It just requires you to recognize that you can never get a sum of 9 when two dice show the same number. As with the MCAT question, the question is simply asking, Do you understand numbers? In this case, do you recognize that the sum of two equal numbers can never be odd…
You get the pattern surely? Hacker’s problem is he is unable to see through the surface gloss of a problem and recognize that in many cases it is just asking the student if she or he has a very basic grasp of number, quantity, and relationships. Yet these are precisely the kinds of abilities he argues elsewhere in the book are crucial in today’s world. He is, I suspect, a victim of the very kind of math teaching he rightly decries—one that concentrates on learning rules and mastering formal manipulations, with little attention to understanding.
My favorite response came from a very perceptive high school students in the New York Times’ letters to the editor (http://www.nytimes.com/2016/02/19/opinion/maths-place-in-the-classroom.html?ref=topics&_r=1):
In “Who Needs Math? Not Everybody” (Education Life, Feb. 7), Andrew Hacker, who teaches quantitative reasoning at Queens College, says that since only 5 percent of people use algebra and/or geometry in their jobs, students don’t need to learn these subjects.
As a high school student, I strongly disagree.
The point of learning is to understand the world. If the only point of learning is job preparation, why should students learn history, or read Shakespeare?
And while your job may never require you to know the difference between a postulate and a theorem, it will almost certainly require other math-based skills, like how to prove something or how to understand a graph. If nothing else, people need math to understand finance, which is a part of everyone’s life.
I also disagree with the logic that if people are failing algebra, then they shouldn’t take algebra. If people approach life that way, they will get nowhere.
Algebra and geometry have a place in the classroom. If students are failing, then the way math is taught may need to change. But what is taught needs no alteration.
Which is crying shame, because Hacker does have good ideas about what a quantitative literacy course should look like (again, from Devlin):
The tragedy of The Math Myth is that Hacker is actually arguing for exactly the kind of life-relevant mathematics education that I and many of my colleagues have been arguing for all our careers. (Our late colleague Lynn Steen comes to mind.) Unfortunately, and I suspect because Hacker himself did not have the benefit of a good math education, his understanding of mathematics is so far off base, he does not recognize that the examples he holds up as illustrations of bad education only seem so to him, because he misunderstands them.
The real myth in The Math Myth is the portrayal of mathematics that forms the basis of his analysis. It’s the same myth you see propagated in Facebook posts from frustrated parents about Common Core math homework their children bring home from school.