Solving Problems Submitted to MAA Journals (Part 6a)

The following problem appeared in Volume 97, Issue 3 (2024) of Mathematics Magazine.

Two points $P$ and $Q$ are chosen at random (uniformly) from the interior of a unit circle. What is the probability that the circle whose diameter is segment $\overline{PQ}$ lies entirely in the interior of the unit circle?

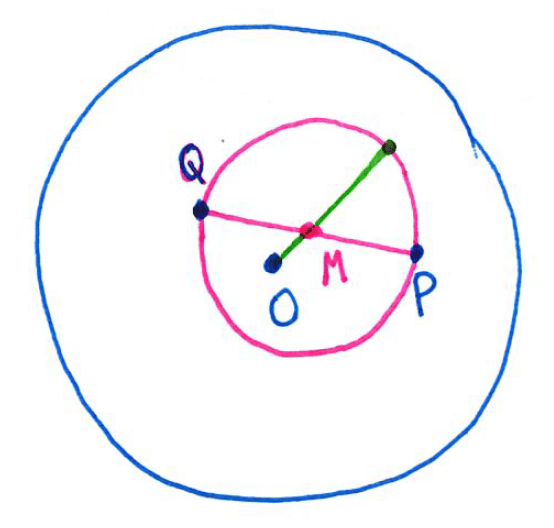
It took me a while to wrap my head around the statement of the problem. In the figure, the points $P$ and $Q$ are chosen from inside the unit circle (blue). Then the circle (pink) with diameter $\overline{PQ}$ has center $M$ , the midpoint of $\overline{PQ}$ . Also, the radius of the pink circle is $MP=MQ$ .

The pink circle will lie entirely the blue circle exactly when the green line containing the origin $O$ , the point $M$ , and a radius of the pink circle lies within the blue circle. Said another way, the condition is that the distance $MO$ plus the radius of the pink circle is less than 1, or

$MO + MP < 1$ .

As a first step toward wrapping my head around this problem, I programmed a simple simulation in Mathematica to count the number of times that $MO + MP < 1$ when points $P$ and $Q$ were chosen at random from the unit circle.

In the above simulation, out of about 61,000,000 attempts, 66.6644% of the attempts were successful. This leads to the natural guess that the true probability is $2/3$ . Indeed, the 95% confidence confidence interval $(0.666524, 0.666764)$ contains $2/3$ , so that the difference of $0.666644$ from $2/3$ can be plausibly attributed to chance.

I end with a quick programming note. This certainly isn’t the ideal way to perform the simulation. First, for a fast simulation, I should have programmed in C++ or Python instead of Mathematica. Second, the coordinates of $P$ and $Q$ are chosen from the unit square, so it’s quite possible for $P$ or $Q$ or both to lie outside the unit circle. Indeed, the chance that both $P$ and $Q$ lie in the unit disk in this simulation is $(\pi/4)^2 \approx 0.617$ , meaning that about $38.3\%$ of the simulations were simply wasted. So the only sense that this was a quick simulation was that I could type it quickly in Mathematica and then let the computer churn out a result. (I’ll talk about a better way to perform the simulation in the next post.)

Solving Problems Submitted to MAA Journals (Part 5e)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

Evaluate the following sums in closed form:

$f(x) = \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

and

$g(x) = \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} - \frac{x^5}{5!} \dots + (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$ .

By using the Taylor series expansions of $\sin x$ and $\cos x$ and flipping the order of a double sum, I was able to show that

$f(x) = -\displaystyle \frac{x \sin x}{2} \qquad \hbox{and} \qquad g(x) = \frac{x\cos x - \sin x}{2}$ .

I immediately got to thinking: there’s nothing particularly special about $\sin x$ and $\cos x$ for this analysis. Is there a way of generalizing this result to all functions with a Taylor series expansion?

Suppose

$h(x) = \displaystyle \sum_{k=0}^\infty a_k x^k$ ,

and let’s use the same technique to evaluate

$\displaystyle \sum_{n=0}^\infty \left( h(x) - \sum_{k=0}^n a_k x^k \right) = \sum_{n=0}^\infty \sum_{k=n+1}^\infty a_k x^k$

$= \displaystyle \sum_{k=1}^\infty \sum_{n=0}^{k-1} a_k x^k$

$= \displaystyle \sum_{k=1}^\infty k a_k x^k$

$= x \displaystyle \sum_{k=1}^\infty k a_k x^{k-1}$

$= x \displaystyle \sum_{k=1}^\infty \left(a_k x^k \right)'$

$= x \displaystyle \left[ (a_0)' + \sum_{k=1}^\infty \left(a_k x^k \right)' \right]$

$= x \displaystyle \sum_{k=0}^\infty \left(a_k x^k \right)'$

$= x \displaystyle \left( \sum_{k=0}^\infty a_k x^k \right)'$

$= x h'(x)$ .

To see why this matches our above results, let’s start with $h(x) = \cos x$ and write out the full Taylor series expansion, including zero coefficients:

$\cos x = 1 + 0x - \displaystyle \frac{x^2}{2!} + 0x^3 + \frac{x^4}{4!} + 0x^5 - \frac{x^6}{6!} \dots$ ,

so that

$x (\cos x)' = \displaystyle \sum_{n=0}^\infty \left( \cos x - \sum_{k=0}^n a_k x^k \right)$

$-x \sin x= \displaystyle \left(\cos x - 1 \right) + \left(\cos x - 1 + 0x \right) + \left( \cos x -1 + 0x + \frac{x^2}{2!} \right) + \left( \cos x -1 + 0x + \frac{x^2}{2!} + 0x^3 \right)$

$\displaystyle + \left( \cos x -1 + 0x + \frac{x^2}{2!} + 0x^3 - \frac{x^4}{4!} \right) + \left( \cos x -1 + 0x + \frac{x^2}{2!} + 0x^3 - \frac{x^4}{4!} + 0x^5 \right) \dots$

After dropping the zero terms and collecting, we obtain

$-x \sin x= \displaystyle 2 \left(\cos x - 1 \right) + 2 \left( \cos x -1 + \frac{x^2}{2!} \right) + 2 \left( \cos x -1 + \frac{x^2}{2!} - \frac{x^4}{4!} \right) \dots$

$-x \sin x = 2 f(x)$

$\displaystyle -\frac{x \sin x}{2} = f(x)$ .

A similar calculation would apply to any even function $h(x)$ .

We repeat for

$h(x) = \sin x = 0 + x + 0x^2 - \displaystyle \frac{x^3}{3!} + 0x^4 + \frac{x^5}{5!} + 0x^6 - \frac{x^7}{7!} \dots$ ,

so that

$x (\sin x)' = (\sin x - 0) + (\sin x - 0 - x) + (\sin x - 0 - x + 0x^2)$

$+ \displaystyle \left( \sin x - 0 - x + 0x^2 + \frac{x^3}{3!} \right) + \left( \sin x - 0 - x + 0x^2 + \frac{x^3}{3!} + 0x^4 \right)$

$+ \displaystyle \left( \sin x - 0 - x + 0x^2 + \frac{x^3}{3!} + 0x^4 - \frac{x^5}{5!} \right) + \left( \sin x - 0 - x + 0x^2 + \frac{x^3}{3!} + 0x^4 - \frac{x^5}{5!} + 0 x^6 \right) \dots$ ,

$x\cos x - \sin x = 2(\sin x - x) + \displaystyle 2\left(\sin x - x + \frac{x^3}{3!} \right) + 2 \left( \sin x - x + \frac{x^3}{3!} - \frac{x^5}{5!} \right) \dots$

$x \cos x - \sin x = 2 g(x)$

$\displaystyle \frac{x \cos x - \sin x}{2} = g(x)$ .

A similar argument applies for any odd function $h(x)$ .

Solving Problems Submitted to MAA Journals (Part 5d)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

Evaluate the following sums in closed form:

$f(x) = \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

and

$g(x) = \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} - \frac{x^5}{5!} \dots + (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$ .

In the previous two posts, I showed that

$f(x) = - \displaystyle \frac{x \sin x}{2} \qquad \hbox{and} \qquad g(x) = \displaystyle \frac{x \cos x - \sin x}{2}$ ;

the technique that I used was using the Taylor series expansions of $\sin x$ and $\cos x$ to write $f(x)$ and $g(x)$ as double sums and then interchanging the order of summation.

In the post, I share an alternate way of solving for $f(x)$ and $g(x)$ . I wish I could take credit for this, but I first learned the idea from my daughter. If we differentiate $g(x)$ , we obtain

$g'(x) = \displaystyle \sum_{n=0}^\infty \left( [\sin x]' - [x]' + \left[\frac{x^3}{3!}\right]' - \left[\frac{x^5}{5!}\right]' \dots + \left[(-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!}\right]' \right)$

$= \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{3x^2}{3!} - \frac{5x^4}{5!} \dots + (-1)^{n-1} \frac{(2n+1)x^{2n}}{(2n+1)!} \right)$

$= \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{3x^2}{3 \cdot 2!} - \frac{5x^4}{5 \cdot 4!} \dots + (-1)^{n-1} \frac{(2n+1)x^{2n}}{(2n+1)(2n)!} \right)$

$= \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

$= f(x)$ .

Something similar happens when differentiating the series for $f(x)$ ; however, it’s not quite so simple because of the $-1$ term. I begin by separating the $n=0$ term from the sum, so that a sum from $n =1$ to $\infty$ remains:

$f(x) = \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

$= (\cos x - 1) + \displaystyle \sum_{n=1}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$ .

I then differentiate as before:

$f'(x) = (\cos x - 1)' + \displaystyle \sum_{n=1}^\infty \left( [\cos x - 1]' + \left[ \frac{x^2}{2!} \right]' - \left[ \frac{x^4}{4!} \right]' \dots + \left[ (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right]' \right)$

$= -\sin x + \displaystyle \sum_{n=1}^\infty \left( -\sin x + \frac{2x}{2!} - \frac{4x^3}{4!} \dots + (-1)^{n-1} \frac{(2n) x^{2n-1}}{(2n)!} \right)$

$= -\sin x + \displaystyle \sum_{n=1}^\infty \left( -\sin x + \frac{2x}{2 \cdot 1!} - \frac{4x^3}{4 \cdot 3!} \dots + (-1)^{n-1} \frac{(2n) x^{2n-1}}{(2n)(2n-1)!} \right)$

$= -\sin x + \displaystyle \sum_{n=1}^\infty \left( -\sin x + x - \frac{x^3}{3!} + \dots + (-1)^{n-1} \frac{x^{2n-1}}{(2n-1)!} \right)$

$= -\sin x - \displaystyle \sum_{n=1}^\infty \left( \sin x - x + \frac{x^3}{3!} + \dots - (-1)^{n-1} \frac{x^{2n-1}}{(2n-1)!} \right)$ .

At this point, we reindex the sum. We make the replacement $k = n - 1$ , so that $n = k+1$ and $k$ varies from $k=0$ to $\infty$ . After the replacement, we then change the dummy index from $k$ back to $n$ .

$f'(x) = -\sin x - \displaystyle \sum_{k=0}^\infty \left( \sin x - x + \frac{x^3}{3!} + \dots - (-1)^{(k+1)-1} \frac{x^{2(k+1)-1}}{(2(k+1)-1)!} \right)$

$= -\sin x - \displaystyle \sum_{k=0}^\infty \left( \sin x - x + \frac{x^3}{3!} + \dots - (-1)^{k} \frac{x^{2k+1}}{(2k+1)!} \right)$

$= -\sin x - \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} + \dots - (-1)^{n} \frac{x^{2n+1}}{(2n+1)!} \right)$

With a slight alteration to the $(-1)^n$ term, this sum is exactly the definition of $g(x)$ :

$f'(x)= -\sin x - \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} + \dots - (-1)^1 (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$

$= -\sin x - \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} + \dots + (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$

$= -\sin x - g(x)$ .

Summarizing, we have shown that $g'(x) = f(x)$ and $f'(x) = -\sin x - g(x)$ . Differentiating $f'(x)$ a second time, we obtain

$f''(x) = -\cos x - g'(x) = -\cos x - f(x)$

$f''(x) + f(x) = -\cos x$ .

This last equation is a second-order nonhomogeneous linear differential equation with constant coefficients. A particular solution, using the method of undetermined coefficients, must have the form $F(x) = Ax\cos x + Bx \sin x$ . Substituting, we see that

$[Ax \cos x + B x \sin x]'' + A x \cos x + Bx \sin x = -\cos x$

$-2A \sin x - Ax \cos x + 2B \cos x - B x \sin x + Ax \cos x + B x \sin x = -\cos x$

$-2A \sin x + 2B \cos x = -\cos x$

We see that $A = 0$ and $B = -1/2,$ which then lead to the particular solution

$F(x) = -\displaystyle \frac{1}{2} x \sin x$

Since $\cos x$ and $\sin x$ are solutions of the associated homogeneous equation $f''(x) + f(x) = 0$ , we conclude that

$f(x) = c_1 \cos x + c_2 \sin x - \displaystyle \frac{1}{2} x \sin x$ ,

where the values of $c_1$ and $c_2$ depend on the initial conditions on $f$ . As it turns out, it is straightforward to compute $f(0)$ and $f'(0)$ , so we will choose $x=0$ for the initial conditions. We observe that $f(0)$ and $g(0)$ are both clearly equal to 0, so that $f'(0) = -\sin 0 - g(0) = 0$ as well.

The initial condition $f(0)=0$ clearly imples that $c_1 = 0$ :

$f(0) = c_1 \cos 0 + c_2 \sin 0 - \displaystyle \frac{1}{2} \cdot 0 \sin 0$

$0 = c_1$

To find $c_2$ , we first find $f'(x)$ :

$f'(x) = c_2 \cos x - \displaystyle \frac{1}{2} \sin x - \frac{1}{2} x \cos x$

$f'(0) = c_2 \cos 0 - \displaystyle \frac{1}{2} \sin 0 - \frac{1}{2} \cdot 0 \cos 0$

$0 = c_2$ .

Since $c_1 = c_2 = 0$ , we conclude that $f(x) = - \displaystyle \frac{1}{2} x \sin x$ , and so

$g(x) = -\sin x - f'(x)$

$= -\sin x - \displaystyle \left( -\frac{1}{2} \sin x - \frac{1}{2} x \cos x \right)$

$= \displaystyle \frac{x \cos x - \sin x}{2}$ .

Solving Problems Submitted to MAA Journals (Part 5c)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

Evaluate the following sums in closed form:

$f(x) = \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

and

$g(x) = \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} - \frac{x^5}{5!} \dots + (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$ .

In the previous post, we showed that $f(x) = - \frac{1}{2} x \sin x$ by writing the series as a double sum and then reversing the order of summation. We proceed with very similar logic to evaluate $g(x)$ . Since

$\sin x = \displaystyle \sum_{k=0}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!}$

is the Taylor series expansion of $\sin x$ , we may write $g(x)$ as

$g(x) = \displaystyle \sum_{n=0}^\infty \left( \sum_{k=0}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!} - \sum_{k=0}^n (-1)^k \frac{x^{2k+1}}{(2k+1)!} \right)$

$= \displaystyle \sum_{n=0}^\infty \sum_{k=n+1}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!}$

As before, we employ one of my favorite techniques from the bag of tricks: reversing the order of summation. Also as before, the inner sum is inner sum is independent of $n$ , and so the inner sum is simply equal to the summand times the number of terms. We see that

$g(x) = \displaystyle \sum_{k=1}^\infty \sum_{n=0}^{k-1} (-1)^k \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \sum_{k=1}^\infty (-1)^k \cdot k \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k \cdot 2k \frac{x^{2k+1}}{(2k+1)!}$ .

At this point, the solution for $g(x)$ diverges from the previous solution for $f(x)$ . I want to cancel the factor of $2k$ in the summand; however, the denominator is

$(2k+1)! = (2k+1)(2k)!$ ,

and $2k$ doesn’t cancel cleanly with $(2k+1)$ . Hypothetically, I could cancel as follows:

$\displaystyle \frac{2k}{(2k+1)!} = \frac{2k}{(2k+1)(2k)(2k-1)!} = \frac{1}{(2k+1)(2k-1)!}$ ,

but that introduces an extra $(2k+1)$ in the denominator that I’d rather avoid.

So, instead, I’ll write $2k$ as $(2k+1)-1$ and then distribute and split into two different sums:

$g(x) = \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k \cdot 2k \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k (2k+1-1) \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty \left[ (-1)^k (2k+1) \frac{x^{2k+1}}{(2k+1)!} - (-1)^k \cdot 1 \frac{x^{2k+1}}{(2k+1)!} \right]$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k (2k+1) \frac{x^{2k+1}}{(2k+1)!} - \frac{1}{2} \sum_{k=1}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k (2k+1) \frac{x^{2k+1}}{(2k+1)(2k)!} - \frac{1}{2} \sum_{k=1}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k \frac{x^{2k+1}}{(2k)!} - \frac{1}{2} \sum_{k=1}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!}$ .

At this point, I factored out a power of $x$ from the first sum. In this way, the two sums are the Taylor series expansions of $\cos x$ and $\sin x$ :

$g(x) = \displaystyle \frac{x}{2} \sum_{k=1}^\infty (-1)^k \cdot \frac{x^{2k}}{(2k)!} - \frac{1}{2} \sum_{k=1}^\infty (-1)^k \frac{x^{2k+1}}{(2k+1)!}$

$= \displaystyle \frac{x}{2} \cos x - \frac{1}{2} \sin x$

$= \displaystyle \frac{x \cos x - \sin x}{2}$ .

This was sufficiently complicated that I was unable to guess this solution by experimenting with Mathematica; nevertheless, Mathematica can give graphical confirmation of the solution since the graphs of the two expressions overlap perfectly.

Solving Problems Submitted to MAA Journals (Part 5b)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

Evaluate the following sums in closed form:

$f(x) = \displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

and

$g(x) = \displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} - \frac{x^5}{5!} \dots + (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$ .

We start with $f(x)$ and the Taylor series

$\cos x = \displaystyle \sum_{k=0}^\infty (-1)^k \frac{x^{2k}}{(2k)!}$ .

With this, $f(x)$ can be written as

$f(x) = \displaystyle \sum_{n=0}^\infty \left( \sum_{k=0}^\infty (-1)^k \frac{x^{2k}}{(2k)!} - \sum_{k=0}^n (-1)^k \frac{x^{2k}}{(2k)!} \right)$

$= \displaystyle \sum_{n=0}^\infty \sum_{k=n+1}^\infty (-1)^k \frac{x^{2k}}{(2k)!}$ .

At this point, my immediate thought was one of my favorite techniques from the bag of tricks: reversing the order of summation. (Two or three chapters of my Ph.D. theses derived from knowing when to apply this technique.) We see that

$f(x) = \displaystyle \sum_{k=1}^\infty \sum_{n=0}^{k-1} (-1)^k \frac{x^{2k}}{(2k)!}$ .

At this point, the inner sum is independent of $n$ , and so the inner sum is simply equal to the summand times the number of terms. Since there are $k$ terms for the inner sum ( $n = 0, 1, \dots, k-1$ ), we see

$f(x) = \displaystyle \sum_{k=1}^\infty (-1)^k \cdot k \frac{x^{2k}}{(2k)!}$ .

To simplify, we multiply top and bottom by 2 so that the first term of $(2k)!$ cancels:

$f(x) = \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k \cdot 2k \frac{x^{2k}}{(2k)(2k-1)!}$

$= \displaystyle \frac{1}{2} \sum_{k=1}^\infty (-1)^k \frac{x^{2k}}{(2k-1)!}$

At this point, I factored out a $(-1)$ and a power of $x$ to make the sum match the Taylor series for $\sin x$ :

$f(x) = \displaystyle -\frac{x}{2} \sum_{k=1}^\infty (-1)^{k-1} \frac{x^{2k-1}}{(2k-1)!} = -\frac{x \sin x}{2}$ .

I was unsurprised but comforted that this matched the guess I had made by experimenting with Mathematica.

Solving Problems Submitted to MAA Journals (Part 5a)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

Evaluate the following sums in closed form:

$\displaystyle \sum_{n=0}^\infty \left( \cos x - 1 + \frac{x^2}{2!} - \frac{x^4}{4!} \dots + (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

and

$\displaystyle \sum_{n=0}^\infty \left( \sin x - x + \frac{x^3}{3!} - \frac{x^5}{5!} \dots + (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$ .

When I first read this problem, I immediately noticed that

$\displaystyle 1 - \frac{x^2}{2!} + \frac{x^4}{4!} \dots - (-1)^{n-1} \frac{x^{2n}}{(2n)!} \right)$

is a Taylor polynomial of $\cos x$ and

$\displaystyle x - \frac{x^3}{3!} + \frac{x^5}{5!} \dots - (-1)^{n-1} \frac{x^{2n+1}}{(2n+1)!} \right)$

is a Taylor polynomial of $\sin x$ . In other words, the given expressions are the sums of the tail-sums of the Taylor series for $\cos x$ and $\sin x$ .

As usual when stumped, I used technology to guide me. Here’s the graph of the first sum, adding the first 50 terms.

I immediately notice that the function oscillates, which makes me suspect that the answer involves either $\cos x$ or $\sin x$ . I also notice that the sizes of oscillations increase as $|x|$ increases, so that the answer should have the form $g(x) \cos x$ or $g(x) \sin x$ , where $g$ is an increasing function. I also notice that the graph is symmetric about the origin, so that the function is even. I also notice that the graph passes through the origin.

So, taking all of that in, one of my first guesses was $y = x \sin x$ , which is satisfies all of the above criteria.

That’s not it, but it’s not far off. The oscillations of my guess in orange are too big and they’re inverted from the actual graph in blue. After some guessing, I eventually landed on $y = -\frac{1}{2} x \sin x$ .

That was a very good sign… the two graphs were pretty much on top of each other. That’s not a proof that $-\frac{1}{2} x \sin x$ is the answer, of course, but it’s certainly a good indicator.

I didn’t have the same luck with the other sum; I could graph it but wasn’t able to just guess what the curve could be.

Solving Problems Submitted to MAA Journals (Part 4)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

Let $A_1, \dots, A_n$ be arbitrary events in a probability field. Denote by $B_k$ the event that at least $k$ of $A_1, \dots A_n$ occur. Prove that $\displaystyle \sum_{k=1}^n P(B_k) = \sum_{k=1}^n P(A_k)$ .

I’ll admit when I first read this problem, I didn’t believe it. I had to draw a couple of Venn diagrams to convince myself that it actually worked:

Of course, pictures are not proofs, so I started giving the problem more thought.

I wish I could say where I got the inspiration from, but I got the idea to define a new random variable $N$ to be the number of events from $A_1, \dots A_n$ that occur. With this definition, $B_k$ becomes the event that $N \ge k$ , so that

$\displaystyle \sum_{k=1}^n P(B_k) = \sum_{k=1}^n P(N \ge k)$

At this point, my Spidey Sense went off: that’s the tail-sum formula for expectation! Since $N$ is a non-negative integer-valued random variable, the mean of $N$ can be computed by

$E(N) = \displaystyle \sum_{k=1}^n P(N \ge k)$ .

Said another way, $E(N) = \displaystyle \sum_{k=1}^n P(B_k)$ .

Therefore, to solve the problem, it remains to show that $\displaystyle \sum_{k=1}^n P(A_k)$ is also equal to $E(N)$ . To do this, I employed the standard technique from the bag of tricks of writing $N$ as the sum of indicator random variables. Define

$I_k = \displaystyle \bigg\{ \begin{array}{ll} 1, & A_k \hbox{~occurs} \\ 0, & A_k \hbox{~does not occur} \end{array}$

Then $N = I_1 + \dots + I_n$ , so that

$E(N) = \displaystyle \sum_{k=1}^n E(I_k) =\sum_{k=1}^n [1 \cdot P(A_k) + 0 \cdot P(A_k^c)] =\sum_{k=1}^n P(A_k)$ .

Equating the two expressions for $E(N)$ , we conclude that $\displaystyle \sum_{k=1}^n P(B_k) = \sum_{k=1}^n P(A_k)$ , as claimed.

Solving Problems Submitted to MAA Journals (Part 3)

The following problem appeared in Volume 53, Issue 4 (2022) of The College Mathematics Journal.

Define, for every non-negative integer $n$ , the $n$ th Catalan number by

$C_n := \displaystyle \frac{1}{n+1} {2n \choose n}$ .

Consider the sequence of complex polynomials in $z$ defined by $z_k := z_{k-1}^2 + z$ for every non-negative integer $k$ , where $z_0 := z$ . It is clear that $z_k$ has degree $2^k$ and thus has the representation

$z_k =\displaystyle \sum_{n=1}^{2^k} M_{n,k} z^n$ ,

where each $M_{n,k}$ is a positive integer. Prove that $M_{n,k} = C_{n-1}$ for $1 \le n \le k+1$ .

This problem appeared in the same issue as the probability problem considered in the previous two posts. Looking back, I think that the confidence that I gained by solving that problem gave me the persistence to solve this problem as well.

My first thought when reading this problem was something like “This involves sums, polynomials, and binomial coefficients. And since the sequence is recursively defined, it’s probably going to involve a proof by mathematical induction. I can do this.”

My second thought was to use Mathematica to develop my own intuition and to confirm that the claimed pattern actually worked for the first few values of $z_k$ .

As claimed in the statement of the problem, each $z_k$ is a polynomial of degree $2^k$ without a nontrivial constant term. Also, for each $z_k$ , the term of degree $n$ , for $1 \le n \le k+1$ , has a coefficient that is independent of $k$ which equal to $C_{n-1}$ . For example, for $z_4$ , the coefficient of $z^5$ (in orange above) is equal to

$C_4 = \displaystyle \frac{1}{5} {8 \choose 4} = \frac{8!}{4! 4! \cdot 5} = \frac{40320}{2880} = 14$ ,

and the problem claims that the coefficient of $z^5$ will remain 14 for $z_5, z_6, z_7, \dots$

Confident that the pattern actually worked, all that remained was pushing through the proof by induction.

We proceed by induction on $k$ . The statement clearly holds for $k=1$ :

$z_1 = z_0^2 + z = z + z^2 = C_0 z + C_1 z^2$ .

Although not necessary, I’ll add for good measure that

$z_2 = z_1^2 + z = (z^2+z)^2 + z = z + z^2 + 2z^3 + z^4 = C_0 z + C_1 z^2 + C_2 z^3 + z^4$

and

$z_3 = z^2 + z = (z^4+2z^3+z^2+z)^2 + z$

$= z + z^2 + 2z^3 + 5z^4 + 6z^5 + 6z^6 + 4z^7 + z^8$

$= C_0 z + C_1 z^2 + C_2 z^3 + C_3 z^4 + 6z^5 + 6z^6 + 4z^7 + z^8.$

This next calculation illustrates what’s coming later. In the previous calculation, the coefficient of $z^4$ is found by multiplying out

$(z^4+2z^3+z^2+z)(z^4+2z^3+z^2+z)$ .

This is accomplished by examining all pairs, one from the left product and one from the right product, so that the exponent works out to be $z^4$ . In this case, it’s

$(2z^3)(z) + (z^2)(z^2) + (z)(2z^3) = 5z^4$ .

For the inductive step, we assume that, for some $k \ge 1$ , $M_{n,k} = C_{n-1}$ for all $1 \le n \le k+1$ , and we define

$z_{k+1} = z + \left( M_{1,k} z + M_{2,k} z^2 + M_{3,k} z^3 + \dots + M_{2^k,k} z^{2^k} \right)^2$

Our goal is to show that $M_{n,k+1} = C_{n-1}$ for $n = 1, 2, \dots, k+2$ .

For $n=1$ , the coefficient $M_{1,k+1}$ of $z$ in $z_{k+1}$ is clearly 1, or $C_0$ .

For $2 \le n \le k+2$ , the coefficient $M_{n,k+1}$ of $z^n$ in $z_{k+1}$ can be found by expanding the above square. Every product of the form $M_{j,k} z^j \cdot M_{n-j,k} z^{n-j}$ will contribute to the term $M_{n,k+1} z^n$ . Since $n \le k+2 \le 2^k+1$ (since $k \ge 1$ ), the values of $j$ that will contribute to this term will be $j = 1, 2, \dots, n-1$ . (Ordinarily, the $z^0$ and $z^n$ terms would also contribute; however, there is no $z^0$ term in the expression being squared). Therefore, after using the induction hypothesis and reindexing, we find

$M_{n,k+1} = \displaystyle \sum_{j=1}^{n-1} M_{j,k} M_{n-j,k}$

$= \displaystyle\sum_{j=1}^{n-1} C_{j-1} C_{n-j-1}$

$= \displaystyle\sum_{j=0}^{n-2} C_j C_{n-2-j}$

$= C_{n-1}$ .

The last step used a recursive relationship for the Catalan numbers that I vaguely recalled but absolutely had to look up to complete the proof.

Solving Problems Submitted to MAA Journals (Part 2b)

The following problem appeared in Volume 53, Issue 4 (2022) of The College Mathematics Journal. This was the second-half of a two-part problem.

Suppose that $X$ and $Y$ are independent, uniform random variables over $[0,1]$ . Define $U_X$ , $V_X$ , $B_X$ , and $W_X$ as follows:

$U_X$ is uniform over $[0,X]$ ,

$V_X$ is uniform over $[X,1]$ ,

$B_X \in \{0,1\}$ with $P(B_X=1) = X$ and $P(B_X=0)=1-X$ , and

$W_X = B_X \cdot U_X + (1-B_X) \cdot V_X$ .

Prove that $W_X$ is uniform over $[0,1]$ .

Once again, one way of showing that $W_X$ is uniform on $[0,1]$ is showing that $P(W_X \le t) = t$ if $0 \le t \le 1$ .

My first thought was that the value of $W_X$ depends on the value of $X$ , and so it makes sense to write $P(W_X \le t)$ as an integral of conditional probabilities:

$P(W_X \le t) = \displaystyle \int_0^1 P(W_X \le t \mid X = x) f(x) \, dx$ ,

where $f(x)$ is the probability density function of $X$ . In this case, since $X$ has a uniform distribution over $[0,1]$ , we see that $f(x) = 1$ for $0 \le x \le 1$ . Therefore,

$P(W_X \le t) = \displaystyle \int_0^1 P(W_X \le t \mid X = x) \, dx$ .

My second thought was that $W_X$ really has a two-part definition:

$W_X = \displaystyle \bigg\{ \begin{array}{ll} U_X, & B_X = 1 \\ V_X, & B_X = 0 \end{array}$

So it made sense to divide the conditional probability into these two cases:

$P(W_X \le t) = \displaystyle \int_0^1 P(W_X \le t, B_X = 1 ~\hbox{or}~ B_X = 0 \mid X = x) \, dx$

$= \displaystyle \int_0^1 P(W_X \le t, B_X = 1 \mid X = x) \, dx + \int_0^1 P(W_X \le t, B_X = 0 \mid X = x) \, dx$

My third thought was that these probabilities can be rewritten using the Multiplication Rule. This ordinarily has the form $P(E \cap F) = P(E) P(F \mid E)$ . For an initial conditional probability, it has the form $P(E \cap F \mid G) = P(E \mid G) P(F \mid E \cap G)$ . Therefore,

$P(W_X \le t) = \displaystyle \int_0^1 P(B_X = 1 \mid X = x) P(W_X \le t \mid B_X = 1, X = x) \, dx$

$+ \displaystyle \int_0^1 P(B_X = 0 \mid X=x) P(W_X \le t \mid B_X = 0, X = x) \, dx$ .

The definition of $B_X$ provides the immediate computation of $P(B_X = 1 \mid X = x)$ and $P(B_X = 0 \mid X = x)$ :

$P(W_X \le t) =\displaystyle \int_0^1 x P(W_X \le t \mid B_X = 1, X = x) \, dx$

$+ \displaystyle \int_0^1 (1-x) P(W_X \le t \mid B_X = 0, X = x) \, dx$

Also, the two-part definition of $W_X$ provides the next step:

$P(W_X \le t) =\displaystyle \int_0^1 x P(U_X \le t \mid B_X = 1, X = x) \, dx$

$+ \displaystyle \int_0^1 (1-x) P(V_X \le t \mid B_X = 0, X = x) \, dx$

We split each of these integrals into an integral from $0$ to $t$ and then an integral from $t$ to $1$ . First,

$\displaystyle \int_0^1 x P(U_X \le t \mid B_X = 1, X = x) \, dx$

$= \displaystyle \int_0^t x P(U_X \le t \mid B_X = 1, X = x) \, dx + \displaystyle \int_t^1 x P(U_X \le t \mid B_X = 1, X = x) \, dx$ .

We now use the following: if $0 \le x \le 1$ and $U$ is uniform over $[0,x]$ , then

$P(U \le t) = \displaystyle \bigg\{ \begin{array}{ll} t/x, & t \le x \\ 1, & t > x \end{array}$

We observe that $t > x$ in the first integral, while $t \le x$ in the second integral. Therefore,

$\displaystyle \int_0^1 x P(U_X \le t \mid B_X = 1, X = x) \, dx = \int_0^t x \cdot 1 \, dx + \int_t^1 x \cdot \frac{t}{x} \, dx$

$= \displaystyle \int_0^t x \, dx + \int_t^1 t \, dx$ .

For the second integral involving $V_X$ , we again split into two subintegrals and use the fact that if $V$ is uniform on $[x,1]$ , then

$P(V \le t) = \displaystyle \bigg\{ \begin{array}{ll} 0, & t \le x \\ (t-x)/(1-x), & t > x \end{array}$

Therefore,

$\displaystyle \int_0^1 (1-x) P(V_X \le t \mid B_X = 0, X = x) \, dx$

$=\displaystyle \int_0^t (1-x) P(V_X \le t \mid B_X = 0, X = x) \, dx$

$+ \displaystyle \int_t^1 (1-x) P(V_X \le t \mid B_X = 0, X = x) \, dx$

$= \displaystyle \int_0^t (1-x) \cdot \frac{t-x}{1-x} \, dx + \int_t^1 (1-x) \cdot 0 \, dx$

$= \displaystyle \int_0^t (t-x) \, dx$ .

Combining, we conclude that

$P(W_X \le t) = \displaystyle \int_0^t x \, dx + \int_t^1 t \, dx + \displaystyle \int_0^t (t-x) \, dx$

$= \displaystyle \int_0^t [x + (t-x)] \, dx + \int_t^1 t \, dx$

$= \displaystyle \int_0^t t \, dx + \int_t^1 t \, dx$

$= \displaystyle \int_0^1 t \, dx$

$= t$ ,

from which we conclude that $W_X$ is uniformly distributed on $[0,1]$ .

As I recall, this took a couple days of staring and false starts before I was finally able to get the solution.

Solving Problems Submitted to MAA Journals (Part 2a)

The following problem appeared in Volume 53, Issue 4 (2022) of The College Mathematics Journal. This was the first problem that was I able to solve in over 30 years of subscribing to MAA journals.

Suppose that $X$ and $Y$ are independent, uniform random variables over $[0,1]$ . Now define the random variable $Z$ by

$Z = (Y-X) {\bf 1}(Y \ge X) + (1-X+Y) {\bf 1}(Y<X)$ .

Prove that $Z$ is uniform over $[0,1]$ . Here, ${\bf 1}[S]$ is the indicator function that is equal to 1 if $S$ is true and 0 otherwise.

The first thing that went through my mind was something like, “This looks odd. But it’s a probability problem using concepts from a senior-level but undergraduate probability course. This was once my field of specialization. I had better be able to get this.”

My second thought was that one way of proving that $Z$ is uniform on $[0,1]$ is showing that $P(Z \le t) = t$ if $0 \le t \le 1$ .

My third thought was that $Z$ really had a two-part definition:

$Z = \bigg\{ \begin{array}{ll} Y-X, & Y \ge X \\ 1-X+Y, & Y <X \end{array}$

So I got started by dividing this probability into the two cases:

$P(Z \le t) = P(Z \le t, Y \ge X ~\hbox{or}~ Y < X)$

$= P(Z \le t, Y \ge X ~\hbox{or}~ Z \le t, Y < X)$

$= P(Z \le t, Y \ge X) + P(Z \le t, Y < X)$

$= P(Y-X \le t, Y \ge X) + P(1 - X + Y \le t, Y < X)$

$= P(Y \le X + t, Y \ge X) + P( Y \le X + t - 1, Y < X)$

$= P(X \le Y \le X + t) + P(Y \le X + t - 1)$ .

In the last step, since $0 \le t \le 1$ , the events $Y \le X + t - 1$ and $Y < X$ are redundant: if $Y \le X + t - 1$ , then $Y$ will automatically be less than $X$ . Therefore, it’s safe to remove $Y < X$ from the last probability.

Ordinarily, such probabilities are computed by double integrals over the joint probability density function of $X$ and $Y$ , which usually isn’t easy. However, in this case, since $X$ and $Y$ are independent and uniform over $[0,1]$ , the ordered pair $(X,Y)$ is uniform on the unit square $[0,1] \times [0,1]$ . Therefore, probabilities can be found by simply computing areas.

In this case, since the area of the unit square is 1, $P(Z \le t)$ is equal to the sum of the areas of

$\{(x,y) \in [0,1] \times [0,1] : x \le y \le x + t \}$ ,

which is depicted in green below, and

$\{(x,y) \in [0,1] \times [0,1] : y \le x + t - 1 \}$ ,

which is depicted in purple.

First, the area in green is a trapezoid. The $y-$ intercept of the line $y = x+t$ is $(0,t)$ , and the two lengths of $t$ and $1-t$ on the upper left of the square are found from this $y-$ intercept. The area of the green trapezoid is easiest found by subtracting the areas of two isosceles right triangles:

$latex \displaystyle \frac{(1)^2}{2} – \frac{(1-t)^2}{2} = \frac{1-1+2t-t^2}{2} = \frac{2t-t^2}{2}.

Second, the area in purple is an isosceles right triangle. The $y-$ intercept of the line $y=x+t-1$ is $(0,t-1)$ , so that the distance from the $y-$ intercept to the origin is $1-t$ . From this, the two lengths of $1-t$ and $t$ are found. Therefore, the area of the purple right triangle is $\displaystyle \frac{t^2}{2}$ .

Adding, we conclude that

$P(Z \le t) = \displaystyle \frac{2t-t^2}{2} + \frac{t^2}{2} = \frac{2t}{2} = t$ .

Therefore, $Z$ is uniform over $[0,1]$ .

A closing note: after going 0-for-4000 in my previous 30+ years of attempting problems submitted to MAA journals, I was unbelievably excited to finally get one. As I recall, it took me less than an hour to get the above solution, although writing up the solution cleanly took longer.

However, the above was only Part 1 of a two-part problem, so I knew I just had to get the second part before submitting. That’ll be the subject of the next post.