Typographical error (perhaps)

Here’s a great typo that I saw on a paper submitted by one of my former students who aspires to be a secondary math teacher. Instead of writing “engaging one’s students,” she accidentally wrote “encaging one’s students.”

Infinite number of monkeys

From Wikipedia:

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare.

This can be formally proven using the second Borel-Cantelli Lemma, a topic which requires measure-theoretic probability. Thus leading me to one of the driest observations that I’ve ever read in a graduate-level textbook, following the proofs of the Borel-Cantelli Lemmas:

The record of a prolonged coin-tossing game is bound to contain every conceivable book in the Morse code [using heads for dot and tails for dash], from Hamlet to eight-place logarithmic tables. It has been suggested that an army of monkeys might be trained to pound typewriters at random in the hope that ultimately great works of literature would be produced. Using a coin for the same purpose may save feeding and training expenses and free the monkeys for other monkey business.

W. Feller, An Introduction to Probability Theory and Its Applications, Volume 1 (Chapter 8.3), page 202.

25 divided by 5 is 14

A good clean joke

Q: How do you tell the difference between an introverted math professor and an extroverted math professor?

A: The extroverted math professor will look at your shoes when talking to you.

Finite simple group of order 2

I like showing this to my students around Valentine’s Day. The singers were math grad students at Northwestern.

Infraction

While I can’t take credit for this one-liner, I’m more than happy to share it.

A colleague was explaining his expectations for simplifying expressions such as

$\displaystyle \frac{\displaystyle ~~~\frac{2x}{x^2+1}~~~}{\displaystyle ~~~\frac{x}{x^2-1}~~~}$

Of course, this isn’t yet simplified, but his students were balking about doing the required work. So, on the spur of the moment, he laid down a simple rule:

Not simplifying a fraction in a fraction is an infraction.

Utterly brilliant.

Ontologically

Case Study #465 of how not to teach a class.

Me: Ontologically, what kind of object is this?

Student: It might help if I knew what “ontologically” meant.

Independence

Once in my probability class, a student asked a reasonable question — could I intuitively explain the difference between “uncorrelated” and “independent”? My expert answer: it’s like the difference between “mostly dead” and “all dead.”

Greek letters

One evening, I was watching the Philadelphia Eagles play the Chicago Bears on NBC’s Sunday Night Football telecast. The bottom of the screen showed the score: “PHI 14 CHI 7.” As my wife walked by, she innocently asked, “Why are there Greek letters on the screen?”

We’ve been fans of $\phi$ and $\chi$ ever since.

Fun with Dimensional Analysis

The principle of diminishing return states that as you continue to increase the amount of stress in your training, you get less benefit from the increase. This is why beginning runners make vast improvements in their fitness and elite runners don’t.

J. Daniels, Daniels’ Running Formula (second edition), p. 13

In February 2013, I began a serious (for me) exercise program so that I could start running 5K races. On March 19, I was able to cover 5K for the first time by alternating a minute of jogging with a minute of walking. My time was 36 minutes flat. Three days later, on March 22, my time was 34:38 by jogging a little more and walking a little less. During that March 22 run, I started thinking about how I could quantify this improvement.

On March 19, my rate of speed was

$\displaystyle \frac{5000 \hbox{~m}}{36 \hbox{~min}} = \frac{5000 \hbox{~m}}{36 \hbox{~min}} \times \frac{1 \hbox{~min}}{60 \hbox{~sec}} \approx 2.3148 \hbox{~m/s}$ .

On March 22, my rate of speed was

$\displaystyle \frac{5000 \hbox{~m}}{34 \times 60 + 38 \hbox{~sec}} \approx 2.4062\hbox{~m/s}$ .

That’s a change of $2.4062 - 2.3148 \approx 0.0913 \hbox{~m/s}$ over 3 days (accounting for roundoff error in the last decimal place), and so the average rate of change is

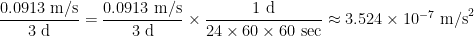$\displaystyle \frac{0.0913 \hbox{~m/s}}{3 \hbox{~d}} = \frac{0.0913 \hbox{~m/s}}{3 \hbox{~d}} \times \frac{1 \hbox{~d}}{24 \times 60 \times 60 \hbox{~sec}} \approx 3.524 \times 10^{-7} \hbox{~m/s}^2$ .

By way of comparison, imagine a keg of beer floating in space. The specifications of beer kegs vary from country to country, but I’ll use the U.S. convention that the mass is 72.8 kg and its height is 23.3 inches = 59.182 cm. Also, for ease of calculation, let’s assume that the keg of beer is a uniformly dense sphere with radius 59.182/2 = 29.591 cm. Under this assumption, the acceleration due to gravity near the surface of the sphere is the same as the acceleration 29.591 cm away from a point-mass of 72.8 kg. Using Newton’s Second Law and the Law of Universal Gravitation, we can solve for the acceleration:

$ma = \displaystyle \frac{GMm}{r^2}$ ,

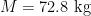where $G \approx 6.67384 \times 10^{-11} \hbox{~m}^3/\hbox{kg} \cdot \hbox{s}^2$ is the gravitational constant, $M = 72.8 \hbox{~kg}$ is the mass of the beer keg, $r = 0.29591 \hbox{~m}$ is the distance of a particle from the center of the beer keg, $m$ is the mass of the particle, and $a$ is the acceleration of the particle. Solving for $a$ , we find

$a = \displaystyle \frac{6.67384 \times 10^{-11} \times 72.8}{0.29591^2} \approx 5.5487 \times 10^{-8} \hbox{~m/s}^2$ .

Since this is only an approximation based on a hypothetical spherical keg of beer, let’s round off and define 1 beerkeg of acceleration to be equal to $5.5 \times 10^{-8} \hbox{~m/s}^2$ .

With this new unit, my improvement in speed from March 19 to March 22 can be quantified as

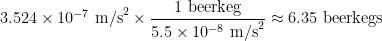$\displaystyle 3.524 \times 10^{-7} \hbox{~m/s}^2 \times \frac{1 \hbox{~beerkeg}}{5.5 \times 10^{-8} \hbox{~m/s}^2} \approx 6.35 \hbox{~beerkegs}$ .

I love physics: improvements in physical fitness can be measured in kegs of beer.

I chose the beerkeg as the unit of measurement mostly for comedic effect (I’m personally a teetotaler). If the reader desires to present a non-alcoholic version of this calculation to students, I’m sure that coolers of Gatorade would fit the bill quite nicely.

For what it’s worth, at the time of this writing (June 7), my personal record for a 5K is 26:58, and I’m trying hard to get down to 25 minutes. Alas, my current improvements in fitness have definitely witnessed the law of diminishing return and is probably best measured in millibeerkegs.