Engaging students: Proving that the angles of a convex n-gon sum to 180(n-2) degrees

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Jessica Trevizo. Her topic, from Geometry: Proving that the angles of a convex $n$ -gon sum to $180(n-2)$ degrees.

E.1 How can technology be used to effectively engage students with this topic?

This website allows the students to see that any polygon, whether regular, concave, or convex, the sum of the interior angles will not change. The students are able to drag any angle of their choice and either enlarge, shrink, or rotate the figure. As the student is able to change the figure, the angles automatically change and are shown on the right hand side of the screen. All of the angles are color coordinated so students are able to easily observe which angle measure goes with the corresponding angle they are moving. Also, this activity allows the students to explore with six different polygons which include the triangle, quadrilateral, pentagon, hexagon, heptagon, and octagon. The triangle and the quadrilateral include an animated clip which consists of a visual proof for the value of the angle sum. It is a simple proof that students will be able to see and understand at their level.

http://illuminations.nctm.org/Activity.aspx?id=3546

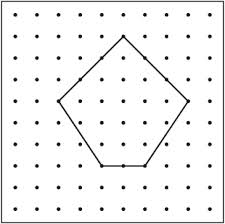
A1. How could you as a teacher create an activity or project that involves your topic?

Using geoboards will help the students derive the sum of interior angles formula on their own. For the activity every student will need a geoboard and a couple of rubber bands. The students will be asked to create a specific shape on the geoboard using the rubber bands. Once every student has completed the figure they will be asked to dissect the figure into triangles. Whenever the teacher gives the students the task he/she needs to make sure to state the rules before they begin. The rules are that the rubber bands cannot cross each other, and the rubber bands must start and end at a vertex of the figure. The students will need to fill out the worksheet provided in the link below. The worksheet is arranged to help them see the pattern after they do a couple of examples with different shapes. The goal is to try to help the student realize that the number of triangles that can be created in a certain figure will be (n-2), n being the number of sides. A higher level question for the students could be, “Why are you only able to create (n-2) triangles?”

http://www.scribd.com/doc/60173215/2-4-Finding-the-sum-of-interior-angles-of-polygons-Worksheet

D1. What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?

Euclid was a famous Greek mathematician that enjoyed the beauty of mathematics. He created a book called Euclid’s Elements where he gathered the knowledge of other famous mathematicians about the logical development of geometry. Pythagoras, Aristotle, Eudoxus, and Thales were some of the other men that influenced his work. Euclid’s Elements is compressed of 13 different volumes that are filled with geometrical theories. He proved the theories by using definitions as well as the axioms used in math.

Euclid was known as the “Father of Geometry” because he discovered geometry and gave it its value. The book contains over 467 propositions and they all include their proof. One of his propositions is about interior and exterior angles which is relevant to the sum of the interior angles topic. Proposition 32 states that an exterior angle is equal to the sum of the two opposite interior angles of a triangle, as well as the three interior angles of a triangle add up to two right angles. Since Euclid proves that a triangle is equal to 180ᵒ, it proves why we need to multiply (n-2)*180.

Engaging students: Introducting translation, rotation, and reflection of figures

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Isis Flores. Her topic, from Geometry: introducing translation, rotation, and reflection of figures.

B2: How does this topic extend what your students should have learned in previous courses?

In order for students to be able to be successful understanding, performing, and identifying translations, rotations and reflections there are a few things that they must have a grasp on from previous classes. Included in these topics is understanding the Cartesian plane and the different relationships between each quadrant. Knowledge of the plane will be extended when students began to work with different degrees of rotations around the plane. Students should also be able to perform several different tasks on the plane such as, plotting points and lines. Being able to perform such tasks will ease the transition of now working with more complex shapes on the plane. Since the topic deals with transformations of figures students must also have an understanding of the basic geometric figures and their different characteristics and classifications. Having a base knowledge of geometric shapes will aid the students when comparing different types of transformations. In previous courses students should also have acquired knowledge of the basic mathematical operations, (addition, subtraction, multiplication, division), which will enable them to perform specific dictated transformations better. The concept of basic mathematical operations will be extended to students as they explore how these operations may play out on a coordinate plane with geometric figures.

C2. How has this topic appeared in high culture (art, classical music, theatre, etc.)?

In any classroom there is always a variety of students with a variety of interests. One of these interests may include art, which can lend itself quite easily to the exploration of different transformations. A specific type of art which uses translations, rotations and reflections is called Geometric Abstraction. Geometric Abstraction became widely popular in the early 20^th century making it an even closer connection for students. The art form uses different types of geometric shapes to create abstract and quite modern looking pieces of work. The fact that the art form is quite new compared to other forms of art does not prevent pieces from being high end items, and the monetary aspect may be another way to engage students. Showing students different pieces of art which were composed using geometric transformations and also showing how highly priced they are, is a great way to show the relevancy and demand for the topic.

A2. How could you as a teacher create an activity or project that involves your topic?

As a teacher at times it is difficult to get students motivated and excited about a specific topic. A great way to give students motivation towards an activity is to give them a bit of autonomy. For translations, rotations and reflections a project that students may perform may be their own art work which would display their knowledge of the content. To even personalize the project even more students may be ask to include an object which is personal to them, for example if a student play soccer then a soccer ball would be an appropriate object for their art work. Students may be asked to also provide directions on their art work so that a classmate may replicate it. Perhaps to take a step further students may analyze each other’s art pieces and try to figure out what order of transformations created the finished piece. For students who may not feel as artistically inclined, or even as another class project, the option of going and finding a real life depiction of transformations may be offered. Students should provide evidence of their findings with an image. The task can be furthered challenged by asking students to find something in their school which depicts transformations. The first project will require students to show their proficiency in performing the transformation, while the second will call on them to show their understanding of what each transformation looks like.

References:

http://www.artspace.com/assume_vivid_astro_focus/starburst

http://www.artspace.com/magazine/art_101/art_101_geometric_abstraction

Engaging students: Finding the area of a square or rectangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Juan Guerra. His topic, from Geometry: finding the area of a square or rectangle.

E1. How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

The website below contains an activity that relates both perimeter and area. In particular, the activity stimulates the student’s mind by making them think of a way to get the amount of fencing that they would need in order to build the stable for animals. After the character in the game learns about perimeter, he is made to think about the area that would be created from the stable. Then the activity mentions the different possibilities of getting the same perimeter but at the same time, the area of each different possibility is also analyzed. The activity makes students realize that even though all stables have the same perimeter, the area was different most of the time. The activity also has the students practice taking measurements and finding the perimeter and area of rectangles. This activity targets multiple objectives and skills because students learn about perimeter, area, and go over measuring the sides with a virtual ruler. This website contains more interactive games that target multiple skills, which will be helpful to the teachers when planning a lesson. Aside from having interactive games, the website also contains videos on tutorials for some basic computations or definitions of terms in math.

http://www.mathplayground.com/area_perimeter.html

F3. How did people’s conception of this topic change over time?

Ancient civilizations have known how to compute the area of basic figures including the square and the rectangle. These civilizations include the Egyptians, Babylonians, and Hindus. The Babylonians actually had a different formula for the area of a square or rectangle. The formula we know today is a*b, where a and b are the lengths of the figure. The Babylonian formula for multiplying two numbers, which was essentially the same as finding the area was [(a + b)2 – (a – b)2]/4. Looking at the formula, it is clear that they had a different perception of what it was to find the product of two numbers and also the area of a square or rectangle. It turns out that the Babylonians were the only ones who used a different formula for the area of a rectangle or square, which means that they saw area differently than the other two civilizations. Another person that represented area was Euclid. In his book named Euclid’s Elements, he showed how multiplying two numbers would look geometrically, which was by taking a segment with length a and another segment with length b and putting them together so that they form a right angle at the ends and completing the rectangle by adding the other two missing sides. This method was used for visualizing the multiplication of numbers but it was also the representation of what area looked like geometrically although Euclid did not mention in his book that this was called area.

http://en.wikipedia.org/wiki/Egyptian_geometry

http://www-history.mcs.st-and.ac.uk/HistTopics/Babylonian_mathematics.html

B1. How can this topic be used in your students’ future courses in mathematics or science?

In the future, students will need to know the concept of area in general in order to solve other types of problems in courses like calculus. To illustrate a better example, suppose you have the equation $y = x$ . What if you wanted a student to find the area of the triangle formed on the interval from 0 to 5? It would seem obvious that when the student graphs it and creates the triangle from that interval, he or she would use the formula for the area of a triangle once they are able to find the base and the height of the triangle. Another example where they would have to find the area of a rectangle would be when they have an equation like $y = 5$ . Let’s say that you wanted to find the area of the rectangle formed from 0 to 4. The student would naturally use the formula that has been known to them for a long time and plug in the numbers. So what if we asked them to find the area of the function $y = x^2$ from 0 to 10? Would the student be able to use the formulas for area that he or she knows? This is where the concept of integration can be introduced to the student. The student might develop the curiosity of wanting to find out how it would be possible to find the area under a curve since the formulas for area that he or she has known all along do not apply. This is only one example where area can be seen in future courses but it seems like an activity like this would naturally lead into integration in a calculus class.

Engaging students: Area of a triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Erick Cordero. His topic, from Geometry: finding the area of a triangle.

B1. How can this topic be used in your students’ future courses in mathematics or science?

Students in high school usually take geometry during the first or second year, and after that they might not see it again until college. Three years might be the wait until a student sees geometry again, nevertheless, geometry does come back in the form of trigonometry. Trigonometry is a class taken right before pre-calculus and it is here where students truly see geometry again. The importance of the triangle in geometry is enormous and in fact, there would not be any trigonometry if it were not because of triangles. Students learn in this class different ways of getting the area of a triangle because they are no longer given the height and the length of the base, now students are given angles or other information and they have to somehow find the area. The topic of area is also used throughout college in math classes, although we are not always finding the area of a triangle, we are nonetheless finding the area of something. To make everything even better, those students who decide to become teachers have to take a course called foundations of geometry. Now it is here were the student really understands the triangles and the axiomatic method of doing proofs.

D1. What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?

http://www.britannica.com/EBchecked/topic/194880/Euclid

http://aleph0.clarku.edu/~djoyce/java/elements/toc.html

In ancient Greece, mathematicians did not deal with the concept of area as we do today. In fact, numbers were not used in geometry and mathematicians had other creative ways of expressing algebraic expression. The great mathematician, Euclid, whom was born in 300 BC, would be the person who would unify all the geometry that was around at the time. Euclid’s greatest contributions and perhaps the most famous book in the history of mathematics, The Elements, is a book that for hundreds of years was the standard way of doing geometry. Euclid’s approach is what is referred to as axiomatic geometry in which one proves geometric expression on the basis on a few assumptions that are assumed to be obvious. In many of his proofs, Euclid compares different triangles in order to learn more about the situation or scenario he is trying to prove. Euclid has a nice way of defining the area of a triangle. He first proves that one can construct a parallelogram and then he proves that two triangles fit into this parallelogram, and thus the area of a triangle is half a parallelogram.

Thus, Euclid defines the area of a triangle in terms of parallelograms. He proves this by using the basic properties of a parallelogram, such as the fact the opposite angles and sides are congruent, to prove that in fact two congruent triangles can fit into a parallelogram.

E. How can technology be used to effectively engage students with this topic?

http://aleph0.clarku.edu/~djoyce/java/elements/toc.html

The website above is a great website for high school students to look at, but because of the language (sounds ancient) I would prefer to go and explore this website with the students. This website contains Euclid’s elements and although the students would not be expect to know how to do all the proofs, I would expect them to know how to prove the formula for the area of a triangle using Euclidian methods. I think the history that this website contains is amazing and it also has diagrams of the way Euclid did his proofs and students like pictures, especially with math, so this would be good. The wording on the website could cause students some problems but for the immense knowledge they can learn from visiting this website, I believe its worth it. Students will get introduce to this beautiful way of proving geometric theorems, methods that were developed hundreds of years ago and are still being used in universities today. I believe this is something incredibly amazing and every student in geometry should at least be familiar with this method of proving things. I believe students will enjoy this way of doing proofs because it is new (it is new to them) and it is not so rigid and mechanical as algebra might have seemed to them. Also, I believe it is only right that they get to know, from reading some of the proofs, who this great mathematician that we know as Euclid was and the immense influence he had in the history of mathematics.

Engaging students: Using the undefined terms point, line, and plane

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Dorathy Scrudder. Her topic, from Geometry: using the undefined terms point, line, and plane.

A1. What interesting word problems using this topic can your students do now?

“Given the marching band coordinates shown in the picture, plot the points on the Cartesian coordinate plane and connect the points to show the line of where the band member will march.” This is an engaging warm up problem for the students because the problem covers all three aspects of the topic while engaging the students who are not normally the subject of the example. Normally, as teachers, we focus on involving the athletes due to stereotypes but we forget there are other students who are not interested in sports or math so they do not stay engaged in the lesson. Using band coordinates allows the band members to feel appreciated and they also get to help explain the marching process to their classmates who may not know how the band creates such intricate designs on the football field. The students should be able to plot the points on the plane and connect the lines before the main lesson. This will allow the teacher to scaffold the students into making connections between the undefined terms of point, line, and plane.

B1. How can this topic be used in your students’ future courses in mathematics or science?

This topic will be continuously used in every following math class and most science classes. Students will be expected to know how to find an equation of a line and graph the line on a plane in all future math courses. They will also be expected to plot points in both polar and rectangular coordinates. A lesson in using the undefined terms of point, line, and plane will come in use for multiple facets of their educational journey. Learning how to plot points on a plane should come fairly easy at this point. Students should be able to label their x and y axis and therefore can plot points. Graphing lines on a plane is a bit more difficult. Students will need to learn how to find the slope and understand what it means. With that information, the students will be able to graph a line when given two points, a point and a slope, and a y-intercept (a point) and a slope. Students will hopefully be able to transfer this knowledge to other topics and courses.

C2. How has this topic appeared in high culture (art, classical music, theatre, etc.)?

This topic has appeared in high culture through art, theatre, and dance. An artist must know their canvas they are working with. Whether the canvas is an actual canvas, a piece of clay, or a pile of scrap metal they will be welding together, the artist must understand the concept of how points, lines, and planes work together to create a masterpiece. A lighting designer must work with a director of a play to know where to point a spotlight, when to follow an actor walking in a line, and to know what altitude the spotlighted actor would be at (for example, if the actor is on a platform or flying in a harness). A dance choreographer must also be conscientious of points, lines, and planes so that the dancers can create formations that are pleasing to the eye. A dancer must understand points and lines so that he or she can move their body with the music and show the audience the lines and contorts of their body.

Engaging students: Circumference of a circle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Daniel Littleton. His topic, from Geometry: computing the circumference of a circle.

C3: How has this topic appeared in the news?

On January 29, 2014 an internet based publisher of medical news, news-medical.net, published an article as to the link between waist circumference and health risk factors. The article is entitled Waist Circumference Measurements Help to Detect Children and Adolescents with Cardiometabolic Risk. This study was conducted in Spain and concluded that including the measurement of waist circumference in clinical practices, in conjunction with traditional height and weight measurements, will allow an easier detection of risk factors for cardiometabolic disorders in children. Waist circumference is measured by placing a tape measure at the top of the hip bone and wrapping the tape around the body level with the navel. This measurement is the circumference, and this measurement can be used to determine the radius and diameter of a human body by knowing that circumference is equivalent to $2 \pi r$ where $r$ is the radius of the circle. This is certainly not the first use of waist circumference in determining health risk factors published in a medical article, however this is a very recent example. This story may be found at the following link: http://www.news-medical.net/news/20140129/Waist-circumference-measurements-help-to-detect-children-and-adolescents-with-cardiometabolic-risk.aspx.

A1: What interesting word problems using this topic can your students do now?

One example of an engaging word problem utilizing the concept of a circumference is as follows. “Aliens have invaded earth and they are establishing colonies on Earth. You are a member of the human resistance and you need to plant explosive traps for the alien soldiers. You know that you have enough materials to build one large bomb, one mid-size bomb, and one small bomb. The large bomb has an explosive diameter of 100 feet. The blast radius of the small bomb is one-fifth the distance of the large bombs diameter. The mid-size bomb has a blast radius that is 20 feet greater than the radius of the small bomb. What is the blast circumference of each of your bombs?” This problem requires the manipulation of both forms of the formula for circumference, $C=2\pi r$ and $C= \pi d$ where r is equal to the radius and d is equal to the diameter. The circumference of the large bomb can be calculated directly from the information provided in the problem. The circumference of the small bomb requires manipulation of the data provided. First, the diameter of the large bomb is divided by five. This determines the blast radius of the small bomb which can be used to determine the circumference. The blast radius of the mid-size bomb is determined by adding 20 feet to the blast radius of the small bomb, and then using this radius in the formula for circumference. The solutions for the circumference are as follows. Large bomb: $100\pi$ or 314.16 feet, Small bomb: $\latex 40\pi$ or 125.66 feet, Mid-size bomb: $60\pi$ or 188.50 feet. I believe that this problem would present an intriguing challenge to the students.

A2: How could you as a teacher create an activity or project that involves your topic?

An engaging activity that involves the determination of circumference will always need to include the manipulation of circles. One creative way to create circles is to form them through bubbles. The title I have chosen for this activity is “Bubblelicious Circumference.” This activity will require the following materials: bubble solution, straws, rulers, paper, and pencil. First the students will clear their desk surface, after which the instructor will pass out the straws, rulers, and pour approximately one tablespoon of bubble solution on the students’ desk. The instructor will also place a small container with bubble solution inside of it on the students’ desk. The students will first dip the end of the straw that will not go into their mouths into the container with bubble solution inside. Next, the students will place the wet end of the straw into the bubble solution on their desk and gently blow air into the bubble solution. The students will continue to blow air until a bubble forms and pops on their desk. Once the bubble pops it will leave a ring of liquid on the surface of their desk in a near perfect circle. The students will then use the ruler to determine the diameter of the circle that is on their desk. This measurement can then be used to determine both the circumference and the radius of the circle. The students will repeat this process at least 10 times, and as many times as the allotted time for the activity will allow. The circumference data will be recorded for each circle formed by each bubble blown on a piece of paper.

Engaging students: Midpoint formula

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Christine Gines. Her topic, from Geometry: deriving the midpoint formula.

How has this topic appeared in pop culture?

Finding the midpoint between two points is a fairly common situation we find ourselves in daily. Take for example cutting a sandwich into two equal halves. Here you are estimating the midpoint between the ends of the sandwich. Maybe you want the bigger half of the sandwich though. In this case you first find the middle and then move slightly away. Whether we realize it or not, finding midpoints happens all around us and bringing this to students’ attention is crucial for their development of connections.

One way to aid these connections is to demonstrate how midpoints appear in our cultures. In particular, I found a popular music video “Meet Me Half Way” by The Black Eyes Peas. The video/song is about Fergie and Will.I.Am being apart and missing each other. Fergie’s solution is “Can you meet me halfway? Right at the borderline. That’s where I’m gonna wait… for you.” Fergie and Will.I.Am’s beginning locations are the endpoints in this scenario and they will meet at their midpoint. In the video, Fergie has already reached midpoint. Here, her lyrics are “Took my heart to the limit, and this is where I’ll stay. I can’t go any further than this.” This can be interpreted as a unique midpoint. If Fergie goes any further, she will no longer be at the midpoint. Her limit is the one midpoint. At the end of the video, Fergie and Will.I.Am are reunited at their midpoint.

After this connection is made, it could be reinforced by giving students specific coordinates of Fergie and Will.I.Am and asking students to find their midpoint. For example, Fergie and Will.I.Am were shown to be on different planets in the video. So, the teacher could give them the coordinates to Jupiter and the earth. If they succeed with this problem, a follow up could be to find the endpoint when you have Will.I.Am’s endpoint and their midpoint.

How could you as a teacher create an activity or project that involves your topic?

A common issue students face regarding formulas is memorizing them without fully comprehending the formulas. They say, “give a man a fish and you feed him for a day; teach a man to fish and you feed him for a lifetime.” So, let’s not just give students a formula, but teach them how to derive the formula by letting them explore the concepts for themselves. A good activity to let students do this is as follows:

In this activity students will Investigate finding the midpoint of a line segment and derive the formula for the midpoint of two points on a coordinate plane.

Have students work in groups of 3 or 4. Each group will have a sheet of large graph paper, markers, a ruler, dice and a penny.

Procedures:

Students will find two points by rolling dice and tossing penny (Dice represents number and penny represents positive or negative) and plot them.
They will draw a line to connect these two points.
Next, students can use the ruler to estimate where the midpoint should be.
Have students investigate ways to accurately find the midpoint of the segment and challenge them to find a formula as well.

Students can create several graphs so that they can recognize the patterns. By letting them draw and plot their own graph, students will more readily realize that the midpoint is exactly in between the two x-values and the two y-values. This will then hopefully lead students to recall how to find the average of two numbers, which is essentially what the formula is. It is important that students make this connection to their previous knowledge and to guide students through this exploration, teacher can ask leading questions such as:

What could you use to represent the numbers so you can write a formula?
How did you find that midpoint?
Are you sure that is really the midpoint?
How can you find the number in between two different numbers?

I don’t know about you but I’ve always thought the best educational games are the ones that actually feels like a game and not just something your teacher is making you do. This is exactly how the game “Entrapment” by The Problem Site feels like. Entrapment is actually a puzzle game. The object of the game is to create line segments such that all the given dots are midpoints to these segments.

More specifically, every red dot must be the midpoint of a line segment connecting two gray dots on the playing field. In the image above, the player is one move away from finishing since there remains one red circle which is not a midpoint. This puzzle is not only addicting, but it teaches students to recognize the relationship of x and y (individually) to the midpoint. After completely only a few of these puzzles, this relationship becomes part of your strategy, which in turn pushes students further away from memorization and brings them closer to comprehension. This puzzle brings all these educational benefits, yet it just feels like you’re playing a game!

http://www.theproblemsite.com/games/entrapment.asp#.UxF5ImJdXHQ

Engaging students: Defining the terms acute triangle, right triangle, and obtuse triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Brittney McCash. Her topic, from Geometry: defining the terms acute triangle, right triangle, and obtuse triangle.

D2. How was this topic adopted by the mathematical community?

As the students are walking into class, I will already have a picture of just a standard (acute) triangle on the board (be it Promethean or white). As class begins, I will pose the question of, “Who can tell me what we are looking at?” Of course, the students will tell me a triangle. I will then proceed to show two more triangles, an obtuse and then a right triangle and ask the same question. The answer will be the same for each. After I show all three, I will put a picture of all three together and ask the students what some of the differences are in each. Once we state the obvious (That there are angles of bigger and smaller sizes in each), I will then post a picture of Euclid. I will ask if anyone knows who this is. More than likely no one will. I will then proceed to tell my students that in 300 BC this man, Euclid, wrote a book called Elements. In this book. We had 4 sub books that consisted of mainly triangles. When telling this fact I will put emphasis on the word “whole” to show how insane that is. By now, the students should be in awe that someone could write so much about triangles. Then I would state that inside this book, Euclid proved that there were 3 different types of triangles. There is obtuse, right, and acute. We could then discuss as a class what we think each triangle presented at the beginning of class is just by sheer guess, and then see if they were right by then going into the actual discussion of the definition of each term. This is a fun and knowledgeable way to bring in some historical background of what they are learning. This shows that it’s just not going to go away, that it has been around for a while, and is still being thoroughly discussed in classrooms, like ours.

A1. What interesting word problems using this topic can your students do now?

An interesting topic that is still around today, is the Bermuda Triangle. After a brief introduction of the definition of an obtuse, right, and acute triangle, I will pose this problem: (There will be a picture of the Bermuda triangle with points labeled, (posted below).)

You are captain of the ship Euclid and are sailing straight for the Bermuda triangle. Hearing of all the bad things that can happen inside the “triangle,” you want to avoid it as best as you can. Luckily for you, you have a super power. You are able to shift one point of triangle wherever you would like. Using your super power and the knowledge of triangles we discussed previously in class, decide which point you would move, and into what triangle so that you can sail past smoothly. You will need to draw your final result with a justification of why you chose that triangle and point.

This question is not only engaging, but it makes them think abstractly. They have to use their knowledge of triangles and produce a result that fits our discussion. Then not only do they have to draw it, they will need to discuss it as well. Talking about why they chose the method they did, helps students retain and process the information better. Take into account, there are multiple ways to answer this question.

B1. How can this topic be used in your students’ future courses in mathematics or science?

Triangles are such a widely used topic, that it is almost guaranteed you will see them again. Not only will you use them later on in our course (Geometry), but you will be using them in pre-calculus and so forth. The main triangle you will work with in the future is the right triangle. That is why it is so important for you to learn the difference now between the triangles. Later, you will be discover the different ways you can solve for sides and angles with a right triangle, you will be discovering the different properties that come with each triangle, and how you can draw them using circles. But before you can do any of that, you have to start with the basics, like knowing which triangle is which and their definitions. I would then go in to explain that now only would triangles be used in classes, but in the real-world as well. They are everywhere we look, literally. Every time we look, we are looking at a specific angle. In the video games we play, we are always making decisions based off of the angles we can use, it’s how we build things; it’s everywhere! To have a basic understanding of something so usable in our world, would be essential to success!

Resources:

http://en.wikipedia.org/wiki/Triangle

http://www.livescience.com/23435-bermuda-triangle.html

Engaging students: Dilations

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Candace Clary. Her topic, from Geometry: identifying dilations.

How could you as a teacher create an activity or project that involves your topic?

Dilations are types of transformation. One activity that I could create for my students is a matching game. I can create cards with index cards, or sheets of paper that have been cut up, that have pictures on them. Each one will be labeled and the students must classify them as dilations, why they are considered dilations, and how they were dilated. As a follow up to this activity, I could assign a topic to create their own city, or small town. They would be required to draw out their town, as well as model it using common crafts. After they do this, they will need to be able to dilate the buildings, and other such things, to make a life size city. They will not have to make the city with a model, but instead, they will need to make a blue print using their model in mind. On this blue print, they will need to inform me of the size of the dilations.

How can this topic be used in your students’ future courses in mathematics or science?

Dilations can be used in many different subjects. Dilations can be used to find sides of a triangle when learning about the triangle congruence theorems. These can be useful in algebra when finding side lengths of figures. This may not happen very often, but it is displayed in algebra. Another place that it will help, although it may not be math, it will help in math classes for architectural students, as well as help people in construction. Many science classes require science projects that work and simulate something real. Dilations can be used when making these projects because you can’t make a real river, but you can structure something that is a smaller figure to the real thing, same thing as a volcano. With architecture, dilations can help with making blue prints and can help in building these blue prints with dilations in mind. With construction, those are blue prints too. I’m not saying in order to build something you must know how to dilate something, but it will help tremendously.

How has this topic appeared in pop culture?

To get the students engaged in the topic, I could bring up the Disney channel movie ‘Honey I Shrunk The Kids.’ This will bring up a discussion with the kids when I ask them what the dad did with his shrink ray. Some ideas that may come up will be that he made them smaller, and then at the end of the movie he made then bigger, back to normal. But in the people were still the same people, they didn’t change, only the size did. At least I hope that is what happens in the discussion. I could then instruct the students into pretending that they had a shrink ray and ‘shrink’ some shapes, as well as other students. This activity, and their answers will be recorded on a chart that they will turn in at the end of class. They, themselves, can decide what size they want to shrink to, but they have to remember to bring the student back to normal at the end of class. I think this activity will be fun for the kids because they will never forget what a dilation is, since they have been ‘dilated’.

Engaging students: Finding the area of a right triangle

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Andrew Wignall. His topic, from Geometry: finding the area of a right triangle.

What interesting (i.e., uncontrived) word problems using this topic can your students do now? (You may find resources such as http://www.spacemath.nasa.gov to be very helpful in this regard; feel free to suggest others.)

To introduce the topic of the area of a right triangle early in a lesson, we can first examine the area of a rectangle, which students should already know how to do.

Say you have a large rectangular garden, 60 feet wide and 10 feet long. Home Depot sells sod (which is a pre-grown grass on a net that can be spread on the ground) at a rate of $3/square foot. What is the area of the garden, in square feet? How much sod should you order? How much would it cost to cover the entire garden with sod?

Instead of having the entire garden covered with sod, suppose you wanted to cover part of the garden with sod and leave the rest as soil for planting flowers. To make it more visually interesting, you decide to set the sod as a triangle? The sod triangle will have a base of 60 feet and a height of 10 feet. What is the area of this triangle in relation to the area of the entire garden? What is the area of this triangle? How much sod should you order? How much would it cost to cover the triangular area with sod?

Through this activity, we can investigate a relationship between right triangles and rectangles, and also the relation of the area of a triangle compared to the angle of a rectangle.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic? Note: It’s not enough to say “such-and-such is a great website”; you need to explain in some detail why it’s a great website

One tool to show the area of a right triangle quickly and easily is the Area Tool on Illuminations (http://illuminations.nctm.org/Activity.aspx?id=3567). With trapezoids, parallelograms, and triangles available, you can click and drag the three vertices of a triangle and instantly see how the area is affected. You can create a quick table and keep a running tally of the base, height, and area, so you can recalculate in front of the class.

Illuminations has a sample lesson plan available online for discovering the area of triangles, and integrates this tool into the plan. If not using this tool as part of a similar plan, we must understand that this tool will not be great for introducing the lesson, as there is no button to lock onto a right triangle. However, there is a button to lock the height, so when you move the vertex opposite the base, you can see how the area does not change, see how the height can be outside the triangle, and extend the formula for the area of a right triangle to the area of any triangle. This tool can then be used in further lessons when discussing the area of parallelograms and trapezoids.

How can this topic be used in your students’ future courses in mathematics or science?

Since triangles are one of the most basic shapes, the area of triangles comes up time and time again. Triangles will also be used to find the area of more complex polygons, such as hexagons and irregular polygons, by breaking down complex shapes into simple triangles and quadrelaterals. Trigonometry uses right (and non-right) triangles extensively; in Precalculus, we will revisit the area of triangles, and learn how to find the area of triangles without explicitly being given the base and height.

Outside the classroom, the area of a triangle is used extensively in architecture, as triangles are strong, and triangular trusses and frames are used in many steel structures. As the inside empty area of the triangle increases, then the stress on the triangle increases, and architects must take this into consideration.

Triangles are also used in 3d computer graphics, as the 3d shapes they design actually consist of lots of little triangles, and they have to fit textures of a certain size (say 512 pixels x 512 pixels) onto a few triangles, so it is important that they know how and where for these textures to lie.

References

Math is Fun, “Activity: Garden Area”. http://www.mathsisfun.com/activity/garden-area.html

Illuminations: Resources for Teaching Math, “Discovering the Area Formula for Triangles”. http://illuminations.nctm.org/Lesson.aspx?id=1874

Illuminations: Resources for Teaching Math, “Area Tool”. http://illuminations.nctm.org/Activity.aspx?id=3567

Home Depot, http://www.homedepot.com/p/StarPro-Greens-Centipede-Southwest-Synthetic-Lawn-Grass-Turf-Sold-by-15-ft-W-rolls-x-Your-L-2-97-Sq-Ft-Equivalent-RGB7/202025213

Math is Fun, “Heron’s Formula”. http://www.mathsisfun.com/geometry/herons-formula.html

Maths in the City, “Most stable shape – triangle”. http://www.mathsinthecity.com/sites/most-stable-shape-triangle

Andre LaMothe, “Texture Mapping Mania”. http://archive.gamedev.net/archive/reference/articles/article852.html