The antiderivative of 1/(x^4+1): Part 3

This antiderivative has arguable the highest ratio of “really hard to compute” to “really easy to write”:

$\displaystyle \int \frac{1}{x^4 + 1} dx$

To compute this integral, I will use the technique of partial fractions. In yesterday’s post, I used De Moivre’s Theorem to factor the denominator over the complex plane, which then led to the factorization of the denominator over the real numbers.

In today’s post, I present an alternative way of factoring the denominator by completing the square. However, unlike the ordinary method of completing the square, I’ll do this by adding and subtracting the middle term and not the final term:

$x^4 + 1= x^4 + 2x^2 + 1 - 2x^2$

$= (x^2 + 1)^2 - (x \sqrt{2})^2$

$= (x^2 + 1 + x\sqrt{2})(x^2 + 1 - x \sqrt{2})$ .

The quadratic formula can then be used to confirm that both of these quadratics have complex roots and hence are irreducible over the real numbers, and so I have thus factored the denominator over the real numbers:

$\displaystyle \int \frac{dx}{x^4 + 1} = \displaystyle \int \frac{dx}{\left(x^2 - x \sqrt{2} + 1 \right) \left(x^2 + x \sqrt{2} + 1\right)}$ .

and the technique of partial fractions can be applied.

There’s a theorem that says that any polynomial over the real numbers can be factored over the real numbers using linear terms and irreducible quadratic terms. However, as seen in this example, there’s no promise that the terms will have rational coefficients.

I’ll continue the calculation of this integral with tomorrow’s post.

Engaging students: Factoring polynomials

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Banner Tuerck. His topic, from Algebra: factoring polynomials.

A1. What interesting (i.e., uncontrived) word problems using this topic can your students do now?

In relation to a specific case one can generate a word problem well within their students reach by relating the factors of a said quadratic polynomial to the length and width of a rectangle or perfect square. Many online resources, such as http://www.purplemath.com/, offer diverse and elaborate examples one could use in order to facilitate this concept. Nevertheless, this way of viewing a factored polynomial may appear more comfortable to a class because it is applying the students preexisting knowledge of area to the new algebraic expressions and equations. Furthermore, it has been my experience that geometric activities interrelating algebra aid in straying students away from ignoring the variable in an expression as a value.

A garden measuring 12 meters by 16 meters is to have a pedestrian pathway installed all around it, increasing the total area to 285 square meters. What will be the width of the pathway?

The above problem is a prime example pulled from the Purple Math website one could use to illustrate a physical situation in which we need to actually determine the factors in order to formulate a quadratic expression to solve for the width. It should be noted that some of these particular word problems can quickly fall into a lesson relating more towards distributing and foiling factors to form an expanded form equation. However, as an instructor one can easily work backwards from an expanded equation to interpret what the factored form can tell us, say about the garden with respect to the example given above.

B1. How can this topic be used in your students’ future courses in mathematics or science?

Factoring polynomials allows students to further comprehend the properties of these expressions before they are later applied as functions in areas such as mathematics and physics. For example, projectile motion stands as a great real world topic capable of enlightening students further on the factors of the polynomial. Specifically, how these factors come about geometrically and how knowing their role will benefit our understanding of the functions potential real world meaning. Lastly, factoring polynomials and evaluating them as roots during middle and high school mathematics will definitely be used when students approach college level calculus courses in relation to indefinite and definite integrals. The previous are just a few examples of how factoring polynomials plays a role in students’ future courses.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

Doing a simple YouTube search of the phrase “factoring polynomials” allows anyone access to nearly 57,000 videos of various tutors, instructors, and professors discussing factoring and distributing respectfully. I would say that future generations will definitely not be without resources. That is not even to mention the revolutionary computation website that is www.wolframalpha.com. This website in and of itself will allow so many individuals to see various forms of a factored polynomial, as well as the graph, roots (given from factors), domain, range, etc. Essentially, computation websites like Wolfram Alpha are intended to allow students the opportunity to discover properties, relationships, and patterns independently. However, there is a potential risk for such websites to become a crutch the students use in order to get good grades as opposed to furthering their understanding. Similarly, with the advancing technology of graphing calculators students will become more engaged when discussing polynomial factorization for the first time in class. Many modern calculators have the ability to identify roots, give a table of coordinates, trace graphs, etc. Some even have a LCD screen or a backlit display to aid in viewing various graphs. Although, just as with computation engines, calculators could potentially distract students from thinking about their problem solving method by them just letting the calculator take over the calculation process. Therefore, I would suggest using caution regarding how soon calculators are introduced when initially engaging a class in factoring polynomials.

References:

http://www.purplemath.com/

http://www.purplemath.com/modules/quadprob2.htm

http://www.wolframalpha.com/

https://www.youtube.com/results?search_query=factoring+polynomials

Engaging students: Graphs of linear equations

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Nada Al-Ghussain. Her topic, from Algebra: graphs of linear equations.

How could you as a teacher create an activity or project that involves your topic?

Positive slope, negative slope, no slope, and undefined, are four lines that cross over the coordinate plane. Boring. So how can I engage my students during the topic of graphs of linear equations, when all they can think of is the four images of slope? Simple, I assign a project that brings out the Individuality and creativity of each student. Something to wake up their minds!

An individualized image-graphing project. I would give each student a large coordinate plane, where they will graph their picture using straight lines only. I would ask them to use only points at intersections, but this can change to half points if needed. Then each student will receive an Equation sheet where they will find and write 2 equations for each different type of slope. So a student will have equations for two horizontal lines, vertical lines, positive slope, and negative slope. The best part is the project can be tailored to each class weakness or strength. I can also ask them to write the slop-intercept form, point slope form, or to even compare slopes that are parallel or perpendicular. When they are done, students would have practiced graphing and writing linear equations many times using their drawn images. Some students would be able to recognize slopes easier when they recall this project and their specific work on it.

Example of a project template:

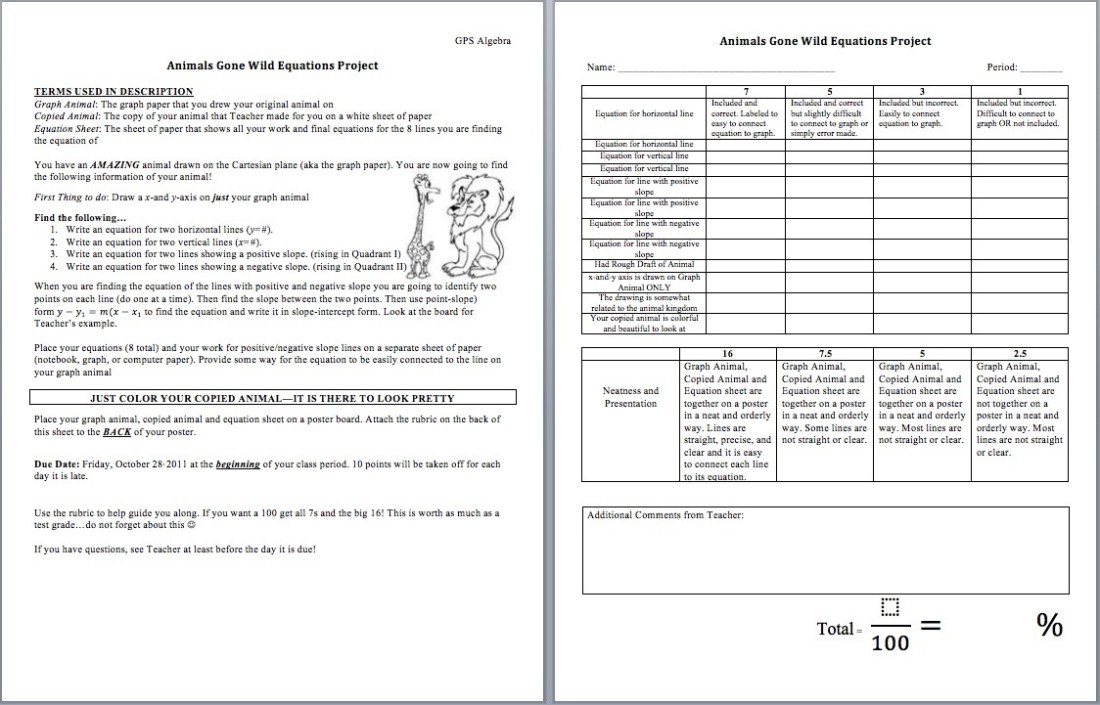
Examples of student work:

How has this topic appeared in the news?

Millions of people tune in to watch the news daily. Information is poured into our ears and images through our eyes. We cannot absorb it all, so the news makes it easy for us to understand and uses graphs of linear equations. Plus, the Whoa! Factor of the slopping lines is really the attention grabber. News comes in many forms either through, TV, Internet, or newspaper. Students can learn to quickly understand the meaning of graphs with the different slopes the few seconds they are exposed to them.

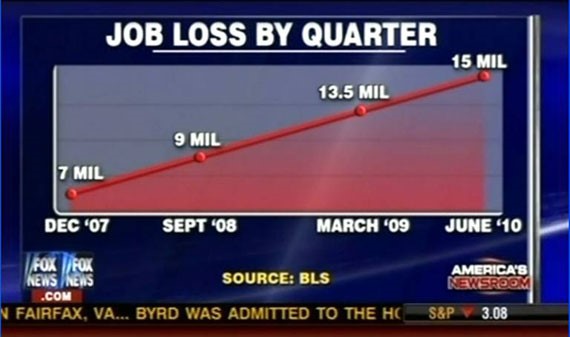
On television, FOX news shows a positive slope of increasing number of job losses through a few years. (Beware for misrepresented data!)

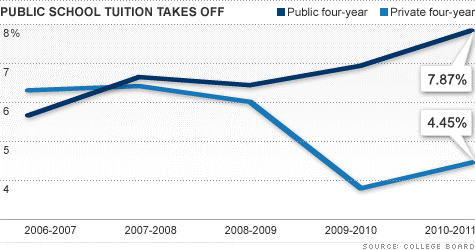
A journal article contains the cost of college increase between public and private colleges showing the negative slope of private costs decreasing.

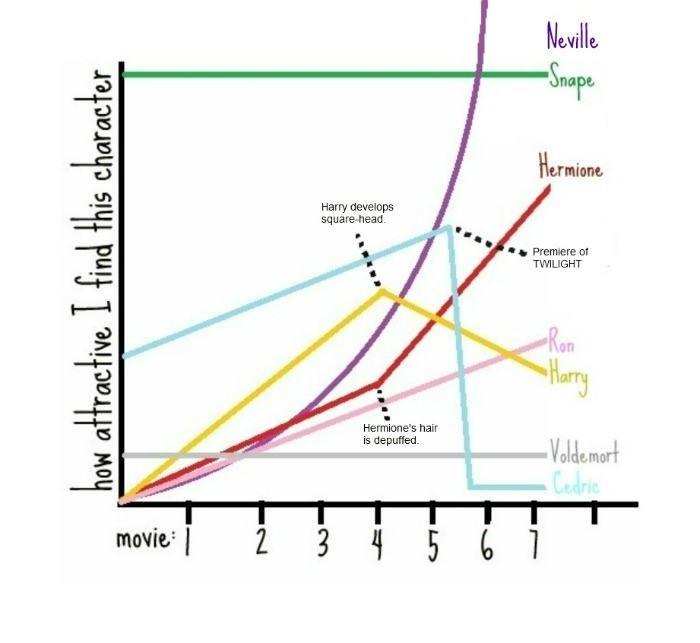
Most importantly line graphs can help muggles, half bloods, witches, and wizards to better understand the rise and decline of attractive characters through the Harry Potter series.

How can this topic be used in your students’ future courses in mathematics or science?

Students are introduced to simple graphs of linear equations where they should be able to name and find the equation of the slope. In a student’s future course with computers or tablets, I would use the Desmos graphing calculator online. This tool gives the students the ability to work backwards. I would ask a class to make certain lines, and they will have to come up with the equation with only their knowledge from previous class. It would really help the students understand the reason behind a negative slope and positive slope plus the difference between zero slope and undefined. After checking their previous knowledge, students can make visual representations of graphing linear inequalities and apply them to real-world problems.

References:

http://www.hoppeninjamath.com/teacherblog/?p=217

http://walkinginmathland.weebly.com/teaching-math-blog/animal-project-graphing-linear-lines-and-stating-equations

http://mediamatters.org/research/2012/10/01/a-history-of-dishonest-fox-charts/190225

http://money.cnn.com/2010/10/28/pf/college/college_tuition/

http://dailyfig.figment.com/2011/07/13/harry-potter-in-charts/

https://www.desmos.com/calculator

Functions that commute (Part 2)

Math With Bad Drawings had a nice post with pedagogical thoughts on the tendency of students to commute two functions that don’t commute:

The author’s proposed remedies:

Teach the distributive law more carefully. Draw pictures. Work examples. Talk about “bags.” Make sure they understand the meaning behind this symbolism.

Teach function notation much more carefully. Give them the chance to practice it. Think like Dan Meyer and seek activities that create the intellectual need for function notation.

Keep stamping out the “everything is linear” error when it crops up. Like the common cold, it’ll probably never be entirely eradicated, but good mathematical hygiene should reduce its prevalence.

I agree with all three points. Concerning the third point, here’s an earlier post of mine concerning these kinds of mistakes (and others), with a one-liner I’ll use to try to get students to remember not to make these kinds of mistakes:

I wish I could remember the speaker’s name, but I heard the following one-liner at a state mathematics conference many years ago, and I’ve used it to great effect in my classes ever since. Whenever I present a property where two functions commute, I’ll say, “In other words, the order of operations does not matter. This is a big deal, because, in real life, the order of operations usually is important. For example, this morning, you probably got dressed and then went outside. The order was important.”
If that fails, then I’ll cite Finding Nemo, trying to minimize frustration by keeping the mood light.

And if that fails, I’ll cite The Princess Bride. One of the most common student mistakes with logarithms is thinking that
$\log_b(x+y) = \log_b x + \log_b y$ .

When I first started my career, I referred to this as the Third Classic Blunder. The first classic blunder, of course, is getting into a major land war in Asia. The second classic blunder is getting into a battle of wits with a Sicilian when death is on the line. And the third classic blunder is thinking that $\log_b(x+y)$ somehow simplfies as $\log_b x + \log_b y$ .

Sadly, as the years pass, fewer and fewer students immediately get the cultural reference. On the bright side, it’s also an opportunity to introduce a new generation to one of the great cinematic masterpieces of all time.

15-year-old catches math error at the Boston Museum of Science

See the full article here: http://www.boston.com/news/local/massachusetts/2015/07/06/year-old-catches-math-error-the-museum-science/awhREamdn1KRg7nz2gGyPO/story.html?p1=Must_Reads

Is 2i less than 3i? (Part 4: Two other attempted inequalities)

In yesterday’s post, I demonstrated that there is no subset $\mathbb{C}^+ \subset \mathbb{C}$ of the complex numbers which satisfies the following four axioms:

If $z_1, z_2 \in \mathbb{C}^+$ , then $z_1+z_2 \in \mathbb{C}^+$
If $z_1, z_2 \in \mathbb{C}^+$ , then $z_1 z_2 \in \mathbb{C}^+$ .
For every $z \ne 0$ , either $z \in \mathbb{C}^+$ or $-z \in \mathbb{C}^+$ , but not both.
$0 \notin \mathbb{C}^+$

However, it’s instructive (and fun) to try to construct such a set. Yesterday I showed that the following subset satisfies three of the four axioms:

$\mathbb{C}^+ = \{x + iy : x > 0 \qquad \hbox{or} \qquad x = 0, y > 0\}$

Apostol’s calculus suggests two other subsets to try:

$\mathbb{C}^+ = \{x + iy : x^2 + y^2 > 0 \}$

and

$\mathbb{C}^+ = \{x + iy : x > y\}$

Neither of these sets work either, but I won’t spoil the fun for you by giving you the proofs. I leave a thought bubble if you’d like to try to figure out which of the four axioms are satisfied by these two notions of “positive” complex numbers.

Is 2i less than 3i? (Part 3: An inequality that almost works)

In yesterday’s post, I demonstrated that there is no subset $\mathbb{C}^+ \subset \mathbb{C}$ of the complex numbers which satisfies the following four axioms:

If $z_1, z_2 \in \mathbb{C}^+$ , then $z_1+z_2 \in \mathbb{C}^+$
If $z_1, z_2 \in \mathbb{C}^+$ , then $z_1 z_2 \in \mathbb{C}^+$ .
For every $z \ne 0$ , either $z \in \mathbb{C}^+$ or $-z \in \mathbb{C}^+$ , but not both.
$0 \notin \mathbb{C}^+$

However, it’s instructive (and fun) to try to construct such a set. One way of attempting this is defining

$\mathbb{C}^+ = \{x + iy : x > 0 \qquad \hbox{or} \qquad x = 0, y > 0\}$

This set $\mathbb{C}^+$ leads to the lexicographic ordering of the complex numbers: if $z_1 = a_1 + i b_1$ and $z_2 = a_2 + i b_2$ , where $a_1, a_2, b_1, b_2 \in \mathbb{R}$ , we say that $z_1 \prec z_2$ if

$a_1 < a_2 \qquad \hbox{or} \qquad a_1 = a_2, b_1 < b_2$

I used the symbol $z_1 \prec z_2$ because, as we’ll see, $\prec$ satisfies some but not all of the usual properties of an inequality. This ordering is sometimes called the “dictionary” order because the numbers are ordered like the words in a dictionary… the real parts are compared first, and then (if that’s a tie) the imaginary parts are compared. See Wikipedia and Mathworld for more information.

In any case, defining $\mathbb{C}^+$ in this way satisfies three of the four order axioms.

Suppose . It’s straightforward to show that . Let and , where . Then , and so .
- Case 1: If $a_1 + a_2 > 0$ , then clearly $z_1 + z_2 \in \mathbb{C}^+$ .
- Case 2: If $a_1 + a_2 = 0$ , that’s only possible if $a_1 = 0$ and $a_2 = 0$ . But since $z_1, z_2 \in \mathbb{C}^+$ , that means that $b_1 > 0$ and $b_2 > 0$ . Therefore, $b_1 + b_2 > 0$ . Since $a_1 + a_2 = 0$ , we again conclude that $z_1 + z_2 \in \mathbb{C}^+$ .
Suppose , where . Then or . We now show that, no matter what, or , but not both.
- Case 1: If $a > 0$ , then $-a < 0$ , and so $z \in \mathbb{C}^+$ but $-z \notin \mathbb{C}^+$ .
- Case 2: If $a < 0$ , then $-a > 0$ , and so $-z \in \mathbb{C}^+$ but $z \notin \mathbb{C}^+$ .
- Case 3: If , then since . Also, if , then , so that and .
  - Subcase 3A: If $b > 0$ , then $-b < 0$ , and so $z \in \mathbb{C}^+$ but $-z \notin \mathbb{C}^+$ .
  - Subcase 3B: If $b < 0$ , then $-b > 0$ , and so $-z \in \mathbb{C}^+$ but $z \notin \mathbb{C}^+$ .
By definition, $0 = 0 + 0i \notin \mathbb{C}^+$ .

However, the fourth property fails. By definition, $i = 0 + 1i \in \mathbb{C}^+$ . However, $i \cdot i = -1 + 0i \notin \mathbb{C}^+$ .

Because this definition of $\mathbb{C}^+$ satisfies three of the four order axioms, the relation $\prec$ satisfies some but not all of the theorems stated in the first post of this series. For example, if $z_1 \prec z_2$ and $z_2 \prec z_3$ , then $z_1 \prec z_3$ . Also, if $z_1 \prec z_2$ and $w_1 \prec w_2$ , then $z_1 + w_1 \prec z_2 + w_2$ .

I’ll leave it to the interested reader to determine which of the theorems are true, and which are false (and have counterexamples).

Is 2i less than 3i? (Part 2: Proof by contradiction)

Is $2i$ less than $3i$ ?

That’s a very natural question for a student to ask when first learning about complex numbers. The short answer is, “No… there isn’t a way to define inequality for complex numbers that satisfies all the properties of real numbers.”

I demonstrated this in a roundabout way in yesterday’s post. Today, let’s tackle the issue using a proof by contradiction. (I almost said, “Let’s tackle the issue more directly,” but avoided that phrase because a proof by contradiction is sometimes called an indirect proof, which would lead to the awkward sentence “Let’s tackle the issue more directly with an indirect proof.”)

Suppose that there’s a subset $\mathbb{C}^+ \subset \mathbb{C}$ of the complex numbers which satisfies the following four axioms:

If $z_1, z_2 \in \mathbb{C}^+$ , then $z_1+z_2 \in \mathbb{C}^+$
If $z_1, z_2 \in \mathbb{C}^+$ , then $z_1 z_2 \in \mathbb{C}^+$ .
For every $z \ne 0$ , either $z \in \mathbb{C}^+$ or $-z \in \mathbb{C}^+$ , but not both.
$0 \notin \mathbb{C}^+$

As discussed yesterday, the ordinary properties of inequalities derive from these four order axioms. Assuming these four order axioms are true for the complex numbers, let’s investigate whether $i$ is “positive” or not. According to the third axiom, either $i \in \mathbb{C}^+$ or $-i \in \mathbb{C}^+$ , but not both.

Case 1. $i \in \mathbb{C}^+$ . Then by the second axiom, $i \cdot i \in \mathbb{C}^+$ , or $-1 \in \mathbb{C}^+$ . Applying the second axiom again, since $i \in \mathbb{C}^+$ and $-1 \in \mathbb{C}^+$ , we have $i \cdot (-1) \in \mathbb{C}^+$ , or $-i \in \mathbb{C}^+$ . But that’s impossible because we assumed that $i \in \mathbb{C}^+$ .

Case 2. $-i \in \mathbb{C}^+$ . Then by the second axiom, $(-i) \cdot (-i) \in \mathbb{C}^+$ , or $-1 \in \mathbb{C}^+$ . Applying the second axiom again, since $-i \in \mathbb{C}^+$ and $-1 \in \mathbb{C}^+$ , we have $(-i) \cdot (-1) \in \mathbb{C}^+$ , or $i \in \mathbb{C}^+$ . But that’s impossible because we assumed that $-i \in \mathbb{C}^+$ .

Either way, we obtain a contradiction. Therefore, there is no subset $\mathbb{C}^+$ of the complex numbers that serves as the “positive” complex numbers, and so there’s no way to define inequalities for complex numbers that satisfies all of the usual properties of inequalities.

Is 2i less than 3i? (Part 1: Order Axioms)

Is $2i$ less than $3i$ ?

However, for this answer to make sense, we need to talk about how inequalities are defined in the first place.

Following Apostol’s calculus, there are four axioms from which the ordinary notions of inequality follow. We shall assume that there exists a certain subset $\mathbb{R}^+ \subset \mathbb{R}$ , called the set of positive numbers, which satisfies the following four order axioms:

If $x, y \in \mathbb{R}^+$ , then $x+y \in \mathbb{R}^+$
If $x, y \in \mathbb{R}^+$ , then $xy \in \mathbb{R}^+$ .
For every real $x \ne 0$ , either $x \in \mathbb{R}^+$ or $-x \in \mathbb{R}^+$ , but not both.
$0 \notin \mathbb{R}^+$

We then define the symbols $<$ , $\le$ , $>$ , and $\ge$ in the obvious way:

$x < y$ means that $y-x$ is positive.
$x > y$ means that $y < x$.
$x \le y$ means that either $x < y$ or $x=y$ .
$x \ge y$ means that $y \le x$

From only these four axioms, many familiar theorems about inequalities can be proven. For what it’s worth, when I was a student in Algebra I, I had to prove nearly all of these theorems.

If $a, b \in \mathbb{R}$ , then exactly one of the following three relations is true: $a < b$ , $a > b$ , $a = b$ .
If $a < b$ and $b < c$ , then $a < c$ .
If $a < b$ , then $a + c < b + c$ .
If $a < b$ and $c > 0$ , then $ac < bc$ .
If $a \ne 0$ , then $a^2 > 0$ .
$1 > 0$ .

We interrupt this list with a public-service announcement: Yes, there’s a proof that $1$ is greater than $0$ . When I tell this to students, I can usually see their heads start to spin, as they think, “Of course we know that!” Then I ask them what the definitions of $1$ and $0$ are. Usually, they have no idea. Then I’ll remind them that $0$ is defined to be the additive identity (so that $x + 0 = x$ and $0 + x = x$ for all real numbers $x$ ), while $1$ is defined to be the multiplicative identity (so that $x \cdot 1 = x$ and $1 \cdot x = x$ for all real numbers $x$ ). Based on those definitions alone, I then ask my students, is it obvious that the multiplicative identity has to be larger than the additive identity? The answer is no, which is why the above order axioms are needed.

Here are some more familiar theorems about inequalities that derive from the four order axioms.

If $a < b$ and $c < 0$ , then $ac > bc$ .
If $a < b$ , then $-a > -b$ .
If $a < 0$ , then $-a > 0$ .
If $ab > 0$ , then $a$ and $b$ are either both positive or both negative.
If $a < c$ and $b < d$ , then $a + b < c + d$ .
If $a < 0$ and $b < 0$ , then $a + b < 0$ .
If $a > 0$ , then $1/a > 0$ .
If $a < 0$ , then $1/a < 0$ .
If $0 < a < b$ , then $0 < 1/b < 1/a$ .
If $a \le b$ and $b \le c$ , then $a \le c$ .
If $a \le b \le c$ and $a = c$ , then $b = c$ .

These last two theorems are less familiar. They basically state that (1) there is no “biggest” real number and (2) there is no positive number that’s immediately to the right of 0.

There is no real number $a$ so that $x \le a$ for all real numbers $x$ .
If $0 \le x < h$ for every positive real number $h$ , then $x =0$ .

Here’s another important theorem that ultimately derives from the four order axioms, proving that a number system including $\sqrt{-1}$ is incompatible with the four order axioms.

There is no real number $x$ so that $x^2 + 1 = 0$ .

The proof of this theorem is simple, given the theorems above. If $x = 0$ , then $x^2 + 1 = 1$ , which is greater than 0. If $x \ne 0$ , then $x^2 > 0$ , and so $x^2 + 1 > 0 + 1 > 1$ . Since $1 > 0$ , it follows by transitivity that $x^2 > 0$ . Either way, $x^2 + 1 > 0$ , and so $x^2 + 1 \ne 0$ .

Proving theorems and special cases (Part 5): Mathematical induction

Today’s post is a little bit off the main topic of this series of posts… but I wanted to give some pedagogical thoughts on yesterday’s post concerning the following proof by induction.

Theorem: If $n \ge 1$ is a positive integer, then $5^n - 1$ is a multiple of 4.

Proof. By induction on $n$ .

$n = 1$ : $5^1 - 1 = 4$ , which is clearly a multiple of 4.

$n$ : Assume that $5^n - 1$ is a multiple of 4, so that $5^n - 1 = 4q$ , where $q$ is an integer. We can also write this as $5^n = 4q + 1$ .

$n+1$ . We wish to show that $5^{n+1} - 1$ is equal to $4Q$ for some (different) integer $Q$ . To do this, notice that

$5^{n+1} - 1 = 5^1 5^n - 1$

$= 5 \times 5^n - 1$

$= 5 \times (4q + 1) - 1$ by the induction hypothesis

$= 20q + 5 - 1$

$= 20q + 4$

$= 4(5q + 1)$ .

So if we let $Q = 5q +1$ , then $5^{n+1} - 1 = 4Q$ , where $Q$ is an integer because $q$ is also an integer.

My primary observation is that even very strong math students tend to have a weak spot when it comes to simplifying exponential expressions (as opposed to polynomial expressions). For example, I find that even very good math students can struggle through the logic of this sequence of equalities:

$2^n + 2^n = 2 \times 2^n = 2^1 \times 2^n = 2^{n+1}$ .

The first step is using the main stumbling block. Students who are completely comfortable with simplifying $x + x$ as $2x$ can be perplexed by simplifying $2^n + 2^n$ as $2 \times 2^n$ . I attribute this to lack of practice with this kind of simplification in lower grade levels.

Here’s another algoebraic stumbling block that I’ve often seen: at the beginning of the $n+1$ case, some students will make the following mistake:

$5^{n+1} - 1 = 5^1 5^n - 1 = 5 (4q) = 4 (5q) = 4Q$ .

Because these students end with a multiple of 4, they fail to notice that the second equality is incorrect since

$5^1 5^n - 1 \ne 5^1 (5^n - 1)$ .

Again, I attribute this to lack of practice with simplifying exponential expressions in lower grade levels… as well as being a little bit over-excited upon seeing $5^n - 1$ and wishing to use the induction hypothesis as soon as possible.