Engaging students: Graphing inequalities

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

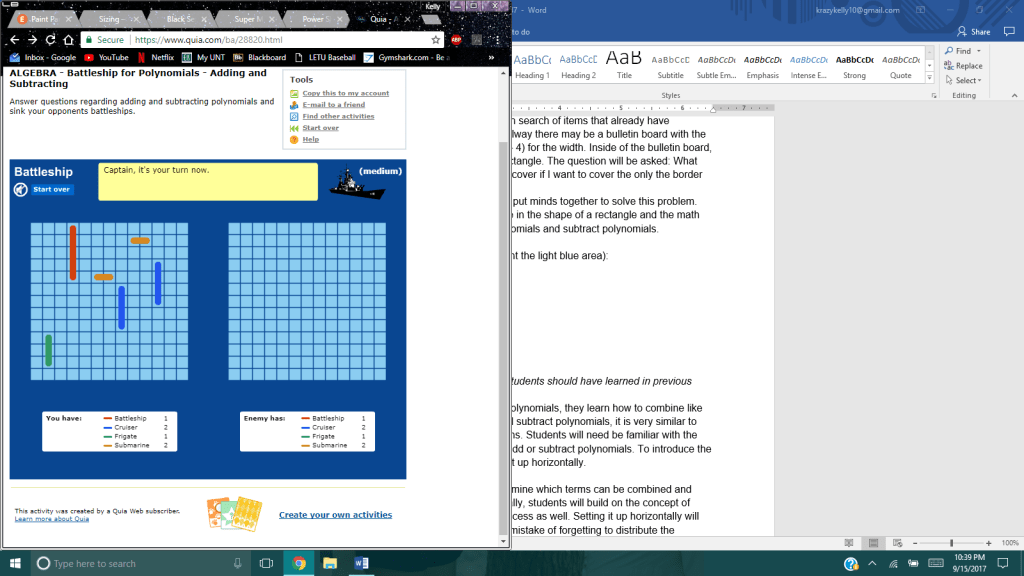
This student submission again comes from my former student Lyndi Mays. Her topic, from Algebra: graphing inequalities.

A1. Once students get to the point where they’re graphing inequalities, they should have a pretty good understanding of how to graph regular functions. I’ve noticed that where students have issues graphing inequalities is knowing which side of the graph should be shaded. Students get confused thinking that the graph should be shaded depending on the direction of the line instead of checking specific points. One activity that I would like to try in the classroom is giving them a worksheet where they graph inequalities on a small graph and when all the little graphs are graphed and shaded it creates a mosaic picture. I feel like there needs to be some sort of pattern or picture so that the students are sure that they’re doing the questions correctly. Another reason I like this activity is because it reaches the intelligence of artistic students. It’s not often that a math lesson can reach artistic intelligences.

C1. One thing the students might find interesting about linear inequalities is that they appeared in the popular TV series, Numbers. In this particular episode, there is a blackout from attacks on an electrical substation. In order to figure out where the attack was located they mapped out where the blackouts were happening. Once they filled in all the different places that were blacking out, they realized it was one big section. Then they drew lines as if the map was on the coordinate plane. From there they are able to target the location where the attack happened.
Students also might be interested in knowing that this is also the way that policeman use to locate a cell phone. They mark the three closest cell towers that the cell phone pinged off of and are then able to draw a section and use linear functions to find the cell phone.

E1. https://us.sofatutor.com/mathematics/videos/graphing-linear-inequalities

This video shows students how to solve for a variable and graph with inequalities. I liked the way it was set up because it was a word problem set up like a story and then solved. I know that students can become intimidated by having to learn new material and then having to apply it to a word problem. But this video kind of walks them through it which I believe could be helpful. Another thing was that the thing we were solving for was very realistic and might help students see why they would need to know how to graph linear equations in the future. The video also showed what x represented (cookies) and what y represented (lemonade). This lets the students know that x and y actually mean something instead of just being an arbitrary variable. I also liked that the video checked for specific points for the shading portion since many students forget that that’s a possibility and end up guessing where to shade.

References:
Sayfan, Sayfan. Graphing Linear Inequalities. https://us.sofatutor.com/mathematics/videos/graphing-linear-inequalities.

Engaging students: Simplifying rational expressions

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Peter Buhler. His topic, from Algebra II/Precalculus: simplifying rational expressions.

A2. How could you as a teacher create an activity or project that involves your topic?

One activity that could be performed when introducing rational expressions is to demonstrate the reason for simplifying. Before teaching students to simplify, instead ask them to evaluate the expressions given various x values. As they struggle through the painstaking process of taking squares, distributing, multiplying, adding and subtracting as they attempt to evaluate the rational expression, take note of how long it may take the students. Then have several students share their method. Following the student sharing, show your efficient method that allows you to simplify the expression before beginning to evaluate.
This not only shows the students that it is quicker, but it often provides more accurate answers to the process that must be taken to “cancel” the terms and then evaluate. Students should be more willing to participate in the following lesson on simplification due to the desire to do less work. This could also be an opportunity to discuss why it is often helpful to look for “shortcuts” or tools that can be used to simplify long or tricky problems into something manageable, even by high school students.

B2. How does this topic extend what your students should have learned in previous courses?

This topic actually extends several previous topics seen in middle school mathematics. One of these topics is reducing fractions. This actually builds on the topic of finding the greatest common factor (GCF), which students learn in elementary school. To reduce a fraction, students find a GCF from both the top and bottom of the fraction, and then simply eliminate that factor leaving the expression in a simplified form. This could be utilized to introduce the idea of simplifying rational expressions, as students will likely be familiar with reducing fractions to their most simplified form.
This can also be applied to multiplying by fractions, as the GCF can be pulled out of the top and bottom of the fractions and simplified, making the multiplication of the fraction simpler. One last possible application could be in solving proportions, as students are typically taught to simplify the proportions before attempting to solve. The common theme in all of these is simplifying in order to make a problem easier and is a more efficient process for most students.

D2. How was this topic adopted by the mathematical community?

There are many advanced applications of simplifying rational expressions. One such function is the Pade approximant, which is an approximation of a rational function of a given order. It was created by Henri Pade in 1890 and has been used to model certain rational functions. While this is certainly an advanced rational expression, it still holds true as there is a polynomial on the top and the bottom, which can be factored and simplified.
Rational functions have also been commonly used to model certain equations in STEM field such as functions of wave patterns for molecular particles, various forces in physics, and other fields that take mathematical ideas and apply them to a science. As a teacher introducing the topic of simplifying these expressions, one could display various applications of these functions and how they are used in a day-to-day setting. Students should be able to see beyond the cut-and-dry steps of simplifying the expressions and understand the implications beyond what they are doing.

References:

If Simplifying Rational Expressions Is Aspirin Then How Do You Create The Headache?

https://en.wikipedia.org/wiki/Rational_function

Engaging students: Solving one- or two-step inequalities

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Michelle Contreras. Her topic, from Algebra: solving one- or two-step inequalities.

A.2 How could you as a teacher create an activity or project that involves your topic?

One way that I could create an activity for my students is by modifying a worksheet that I’ve seen around the internet and make it something enjoyable and engaging for students. The original worksheet is called “Who broke the Vase?” from teacherspayteachers.com and the students are supposed to solve the one and two step inequalities and match the answer with the letter of the question to figure out who broke the vase. The students are to cut the lettered puzzle and match them to the answer. I believe tweaking this worksheet and make it a group scavenger hunt activity will be a good idea because the students will be split into a group of 3 or 4 and each group will have particular letters assigned to solve.

The scavenger hunt will be around the class so the students have an opportunity to work with other students but also to walk around and be active. I will have the lettered puzzle cut into pieces so each group can match their answerers to a letter and put it up in the overhead so everyone can see everyone else’s answers and progress. I believe this 20 minute activity will be best used after a lesson in one or two step inequalities giving the students an opportunity to work with their peers, to ask questions, and to address any misconceptions. This gives the teacher an opportunity to clarify ideas and to see how well students are understanding inequalities.

B.1 How can this topic be used in your students’ future courses in mathematics or science?

Having a good understanding on how to solve for one or two step inequalities is an important skill to acquire. There are many classes that use this concept of inequalities over and over again, so if the foundation of this topic is not set right other math topics and concepts may not make sense. Personally I have made use of my knowledge of inequalities in calculus 1, solving for inequalities trying to prove limits and the squeeze theorem. Last semester in real analysis class there was a theorem called the triangle inequality which just by the name you have an idea of what it’s about. The theorem compares the sum of two lengths of a triangle to the length of the third side. Talking with your students about different instances that you will come across a certain topic may help them want to learn and gain a better understanding.
Comparing inequalities and equations is important and helps the students draw connections and remember better what to do since the properties of inequalities are very similar to equations. Stressing to your students that when you divide by a negative number on both sides that you should always flip the sign is essential. Students struggle to remember this properties since with equations you normally don’t do anything when you divide by a negative number. Having all the properties imbedded into your student’s memory will benefit them and prepare them for the future.

E.1 How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

You Tube in my opinion has great learning videos, which are a great tool for the classroom. Most often than not I refer to You Tube to get a deeper understanding about a topic, even more now that I’m in college. Searching for inequality videos that would be engaging was a pretty tough because I was looking for a precise video that was not only educational but I guess “fun” to watch. The video that I believe is a great tool for the students who are trying to remember all the rules for solving inequalities is called “Inequalities Rap”. This video makes reference to a show that I used to watch when I was little “Power Puff Girls” so automatically it grabbed my attention.
The video which was made by a group of students for a math project contains the voices of the actual students rapping about the properties of inequalities and going over the steps to solve one or two step inequalities. The video is just short of 2 minutes and is very enjoyable to watch which I believe will grab the students attention since there is some rapping/singing involved. I could also ask my students to memorize all the lyrics to the rap song and rap it to the entire class if their up for it. Giving those particular students 5-6 free homework passes that could be used throughout the year.

References
“Who broke the vase?” https://www.teacherspayteachers.com/Product/Solving-One-Step-Equations-Fun-Engaging-Worksheet-Activity-124604

“Inequalities Rap” https://www.youtube.com/watch?v=FpWm_wL73LY

Engaging students: Adding and subtracting polynomials

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Kelly Bui. Her topic, from Algebra: multiplying polynomials.

A2. How could you as a teacher create an activity or project that involves your topic?
The main idea of the activity will be finding an expression to represent the area of the border given the dimensions of the outer rectangle and the inner rectangle. The students will need to know how to multiply binomials and add or subtract polynomials. Therefore, this activity would be towards the end of the unit. Students will be asked to roam around the classroom or the hallway in search of items that already have dimensions labeled. For example, in the hallway there may be a bulletin board with the dimensions (2x² – 7) for the length and (3x – 4) for the width. Inside of the bulletin board, there will be the dimensions of a smaller rectangle. The question will be asked: What expression will represent the area I want to cover if I want to cover the only the border with paper?
Students may work in partners or groups to put minds together to solve this problem. Every object labeled with dimensions will be in the shape of a rectangle and the math involved will require students to multiply binomials and subtract polynomials.

B2. How does this topic extend what your students should have learned in previous courses?
Before students learn to add and subtract polynomials, they learn how to combine like terms such as 3x and 5x. When we add and subtract polynomials, it is very similar to combining like terms in algebraic expressions. Students will need be familiar with the concept of combing like terms before they add or subtract polynomials. To introduce the topic of combining polynomials, it can be set up horizontally.

Such as: (3x² – 5x + 6) – (6x² – 4x + 9)

By setting it up this way, students can determine which terms can be combined and which terms need to be left alone. Additionally, students will build on the concept of combining like terms as it applies to this process as well. Setting it up horizontally will also increase the chance of preventing the mistake of forgetting to distribute the negative sign throughout the second polynomial. Once students are comfortable doing it this way, the addition and subtraction can be set up as a vertical problem where students must now take the step to align the like terms together in order to add or subtract. By taking the step to set up the polynomials horizontally before vertically, it will give the students a deeper understanding of what concept is actually behind adding and subtracting polynomials.

E1. How can technology be used to effectively engage students with this topic?

The website http://www.quia.com provides a multitude of activities relating to different subjects. The game I chose to correlate adding and subtracting polynomials is identical to the actual game Battleship. The game can be played by anyone with access to the internet and Adobe. This game is interactive because you won’t have to perform math on every single shot fired at the enemy. If the student does hit one of the vessels, in order to actually “hit” the enemy’s ship, the student must successfully add or subtract two polynomials. If a student hits a vessel but is unable to solve the polynomial correctly, the game will highlight the hit area so that the student can try again. This game can either engage the students to see who can sink all of the enemy’s ships first, or it can be assigned as a homework assignment that requires showing work and screenshotting the end result of the game. Lastly, you can choose the level of difficulty of the game. For example, on the hard level, you must determine the missing addend or minuend to the expression, or add or subtract polynomials of different degrees.
The website also offers an option to create your own activities, so if Battleship isn’t panning out as desired, it is possible to create your own game for your students.
Game: https://www.quia.com/ba/28820.html

References:

Area of the Border: https://www.sophia.org/concepts/adding-and-subtracting-polynomials-in-the-real-world

Combining Like Terms: https://courses.lumenlearning.com/boundless-algebra/chapter/introduction-to-polynomials/

Battleship: https://www.quia.com/ba/28820.html

Engaging students: Using the point-slope equation of a line

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Rachel Delflache. Her topic, from Algebra: using the point-slope equation of a line.

A2: How could you as a teacher create an activity that involves the topic?

An adaptation of the stained-glass window project could be used to practice the point-slope formula (picture beside). Start by giving the students a piece of graph paper that is shaped like a traditional stained-glass window and then let they students create a window of their choosing using straight lines only. Once they are done creating their window, ask them to solve for and label the equations of the lines used in their design. While this project involves the point slope formula in a rather obvious way, giving the students the freedom to create a stained-glass window that they like helps to engage the students more than a normal worksheet. Also, by having them solve for the equations of the lines they created it is very probable that the numbers they must use for the equation will not be “pretty numbers” which would add an addition level of difficulty to the assignment.

B2: How does this topic extend what your students should have learned in previous courses?

The point-slope formula extends from the students’ knowledge of the slope formula

m = (y2-y1)/(x2-x1)
(x2-x1)m = y2-y1
y-y1 = m(x-x1).

This means that the students could solve for the point-slope formula given the proper information and prompts. By allowing students to solve for the point-slope formula given the previous knowledge of the formula for slope, it gives the students a deeper understanding of how and why the point-slope formula works the way it does. Allowing the students to solve for the point-slope formula also increases the retention rate among the students.

C1&3: How has this topic appeared in pop culture and the news?

Graphs are everywhere in the news, like the first graph below. While they are often time line charts, each section of the line has its own equation that could be solved for given the information found on the graph. One of the simplest way to solve for each section of the line graph would be to use point slope formula. The benefit of using point slope formula to solve for the equations of these graphs is that there is very minimal information needed—assuming that two coordinates can be located on the graph, the linear equation can be solved for. Another place where graphs appear is in pop culture. It is becoming more common to find graphs like the second one below. These graphs are often time linear equation for which the formula could be solved for using the point slope formula. These kinds of graphs could be used to create an activity where the students use the point slope formula to solve to the equations shown in either the real world or comical graph.

References:

Stained glass window-

Stained Glass Window Graphing Project

iPhone sales-
https://www.usatoday.com/story/tech/news/2017/06/28/iphones-smartphone-revolution-4-graphs/103216746/

Halloween graph-
https://www.buzzfeed.com/agh/halloween-charts-and-graphs?utm_term=.hpXrNWPm9#.qpvwGmxp0

Engaging students: Finding the slope of a line

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Deanna Cravens. Her topic, from Algebra: finding the slope of a line.

C3. How has this topic appeared in high culture (art/sports)?

While one might not think of ski jumping as an art but more of a sport, there is definitely an artistic way about doing the jumping. The winter Olympics is one of the most popular sporting events, besides the summer Olympics that the world watches. This is a perfect engage for the beginning of class, not only is it extremely humorous but it is extremely engaging. It will instantly get a class interested in the topic of the day. I would first ask the students what the hill the skiers going down is called. Of course the answer that I would be looking for is the “ski slope.” This draws on prior knowledge to help students make a meaningful connection to the mathematical term of slope. Then I would ask students to interpret the meaning of slope in the context of the skiers. This allows for an easy transition into the topic for finding the slope of a line.

C1. How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?

Look at this scene from Transformers, it shows a perfect example of a linear line on the edge of the pyramid that the Decepticon is destroying. This video easily catches the attention of students because it is from the very popular Transformer movie. I would play the short twenty second clip and then have some student discussion at the beginning of class. This could be done as an introduction to the topic where students could be asked “how can we find the steepness of that edge of the pyrmaid?” Then the students can discuss with a partner and then group discussion can ensue. It could also be done as a quick review, where students are asked to recall how to find the slope of a line and what it determines. The students would be asked to draw on their knowledge of slope and produce a formula that would calculate it.

How can this topic be used in your students’ future courses in mathematics or science?
Finding the slope of a line is an essential part of mathematics. It is used in statistics, algebra, calculus, and so much more. One could say it is an integral part of calculus (pun intended). Not only is it used in mathematics classes, but it is also very relevant to science. One specific example is chemistry. There are specific reaction rates of solutions. These rates are expressed in terms of change in concentration divided by the change in time. This is exactly the formula that is used in math classes to find the slope. However, it is usually expressed in terms of change in y divided by change in x. Slope is also used in physics when working with velocity and acceleration of objects. While one could think of slope in the standard way of ‘rise over run,’ in these advanced classes whether math or science, it usually better thought of as ∆y/∆x.

References:

Engaging students: Solving linear systems of equations with matrices

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Danielle Pope. Her topic, from Algebra II: solving linear systems of equations with matrices.

B2. How does this topic extend what your students should have learned in previous courses?

Based off of the TEKS, matrices are introduced in Algebra 2. In previous math courses, students are already going to learn basic arithmetic from elementary school and solving equations in middle and high school. By the time students get to high school, they should have solving single equations down. This concept is then expanded with a system of equations, which is taught with the help of matrices. A matrix is just an “array of numbers” so that’s why this method of solving can be used with linear equations. Once the matrix is set up there are 2 main ways to solve for the solutions. The one I will be discussing is reduced row echelon form. This method of solving systems utilizes the basic arithmetic that students already know. There are 3 row operations that students already know how to use in general not related to matrices. Those are multiplying a row by a constant, switching two rows, and adding a constant times a row to another row. Even though these specific operations are used for matrices, kids have seen how to multiply 2 constants or variables, switching variables, and adding constants or variables in their previous courses. Matrices just add another element to their basic arithmetic abilities.

D4. What are the contributions of various cultures to this topic?

Matrices have been around for much longer than some people may realize. One of the earliest civilizations that matrices were traced back to were the Babylonians. This was just one of the many contributions that they contributed to mathematics. The Chinese wrote a book, Nine Chapters of the Mathematical Art, Written during the Han Dynasty in China gave the first known example of matrix methods”. During the same era, around 200 BC, a Chinese mathematician Liu Hui solved linear equations using matrices. In the 1800s, Germany started taking a look at matrices. German mathematician, Carl Jacobi, brought the idea of determinants and matrices into the light. Carl Gauss, another German mathematician, took this idea of determinants and developed it. It wasn’t until Augustin Cauchy, a French mathematician, used and defined the word determinant how was use it today. James Sylvester, an English mathematician, “used the term matrix in 1850”. Sylvester also worked with mathematician Arthur Cayley who “first published an abstract definition of matrix” in his memoir on the Theory of Matrices in 1858. This final definition of a determinant is still used today in classrooms to help solve complex system of equations.

E1. How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

In a classroom today, students should be able to access use of a graphing calculator. The matrix feature on these can easily check the work of students just learning how to row-reduce or solve for determinants and inverse matrices. In the classroom, I would use this technology like a race for the right answer to get them engaged in matrices. Give students an easy 2-equation system and have them solve for the variables. Each new problem add an equation or add a variable. While students are solving by hand, the teacher will be using the calculator to see which person can get the answer first. Overtime the problems will be too daunting to do by hand so students will be more engaged to learn this faster shortcut using the calculator. Another resource that can be used out of the classroom is Khan Academies’ videos on solving system of equations with matrices. These videos can be used to fill in any gaps if students have questions at home. These videos can also be used as the lecture in a flipped classroom environment.

References

https://www.mathsisfun.com/algebra/systems-linear-equations-matrices.html
http://www.sparknotes.com/math/algebra2/matrices/section4.rhtml
http://math.nie.edu.sg/bwjyeo/it/MathsOnline_AM/livemath/the/IT3AMMatricesHistory.html

http://math.nie.edu.sg/bwjyeo/it/MathsOnline_AM/livemath/the/IT3AMMatricesHistory.html
http://www.storyofmathematics.com/mathematicians.html

https://www.khanacademy.org/math/precalculus/precalc-matrices/solving-equations-with-inverse-matrices/v/matrix-equations-systems

Engaging students: Parallel and perpendicular lines

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Cody Jacobs. His topic, from Algebra: parallel and perpendicular lines.

D1. What interesting things can you say about the people who contributed to the discovery and/or the development of this topic?

Euclid is one of the most famous mathematicians of all time. His fame rests mostly on his 13 books commonly referred to as Euclid’s Elements. Euclid’s Elements are said to have a greater impact on the human mind that any other book except for the bible. Euclid contributed to the development of this topic based off the fact that his Elements have been used for centuries for teaching foundational geometry. The importance of Euclid’s books come from the minimal assumptions made, and the natural progression from simple results to more complex results. Euclid starts of listing 23 definitions and 5 postulates in which uses to prove theorems. His books contain over 400 theorems and proofs which layout the guidelines for how we use geometry today.

E1. How can technology be used to effectively engage students with this topic?

Desmos.com is a great website website that allows you to pick out activities your students can do. They have some activities regarding parallel and perpendicular lines where students shift the lines to make them parallel or perpendicular. I have used this website before regarding parabolas and students are fully engaged. Desmos has plenty of activities to choose from to find the right fit for your class, so do not be afraid to look around for a while. You can sign in as a teacher and make a code for your students to get into the activity. There are even some word problems so you can get a better understanding of what your students are thinking. I think Desmos is best used at the end of a topic, more as a general review over everything because the activities go through topics pretty fast.

B1. How can this topic be used in your students’ future courses in mathematics or science?

Students will continue to use parallel and perpendicular equations throughout their mathematical career. I am now in vector calculus and I am still using parallel and perpendicular lines in 3-dimensional planes. With that being said parallel and perpendicular lines are not going to disappear as you go further into math, in fact you have to start using different methods to find the parallel and perpendicular lines the farther you go. Soon it will no longer be as simple as duplicating the slope or finding the reciprocal. Parallel and perpendicular lines also play a key part in physics regarding vectors just as they do in vector calculus, when you try to find equilibrium forces.

Engaging students: Approximating data by a straight line

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Caroline Wick. Her topic, from Algebra: approximating data to a straight line.

B1. Curriculum

How can this topic be used in your students’ future courses in mathematics or science?

Though approximating data by a straight line is a subject that is brought up in Algebra 2, it is something that students will need to use in a number of subjects down the line. Probably the most obvious subject would be statistics. Finding an approximate trend line is extremely important for a statistician so that they can predict future, unobserved data. Another example that might not be as readily noticeable would be anthropology. Anthropology is the study of humans in various parts of life. In this case, according to Brian Hopkins, anthropology can be used by stores to figure out what types of products they should stock on their shelves during different types of the year. They do this by collecting the data, then approximating the trend lines to predict how the product will sell during the same season of the next year. For example, Orange Juice and tissues are known to be sold more often during the winter seasons, so stores know that they want to stock up on orange juice and tissue during the colder season each year.

A1: Applications

What interesting (i.e., uncontrived) word problems using this topic can your students do now?
Using the data given below:
(a) plot the points on a graph
(b) Then, using a ruler, do your best to approximate a trend line that fits the points
(c) Write an equation (y=mx+b) that best fits the trend line
(d) Approximate the next four numbers on the line using the equation you created.

Population growth in squirrels in TX from 1950-1980 (in millions)*
Year (x) 1950 1955 1960 1965 1970 1975 1980
Pop. (y) 12 12.7 13.1 13 13.6 13.7 14

From here the student would create his/her graph with the plotted points, find a line that best fits the points with equal numbers over and under the line. They would then use the data and the line to find an equation that best fits the scatter plot data that they graphed. They would then find the approximate squirrel population for 1985, 1990, 1995, and 2000.

This could be either an assignment or it could turn into a project for students with different sets of data. Students could even collect their own data to formulate the graph and equation.

*not real data, fabricated for this problem specifically.

Culture
How has this topic appeared in pop culture (movies, TV, current music, video games, etc.)?

The approximation of data through trend lines has been used in pop culture since the birth of popular culture in the mid twentieth century. More relevantly, it is used to map certain cultural trends. When a new movie is coming out, statisticians use previous data from people who watched/reviewed the movie before its release to map out how they believe it will be appreciated by the public. A movie that did will before its release will likely have a positive trend line that continues upward at a somewhat steady rate. It will get more tickets at the box office than a movie that was not as well liked that might have a less-steep slope. Statisticians use this same trend approximation with TV shows and whether they should run another season, or in music when it hits the top of the charts. The more people listen to a song, the more likelihood it has to be listened to other people, thus the trend continues upward until is slowly dies off.

Take for instance, Taylor Swift’s “Look What You Made Me Do” that was released August 25th of this year. From its release and popularity, statisticians were able to track the data and predict that the song would be number 1 on the top 100 just a few weeks after its release.

References:

B1: https://www.cio.com/article/2372429/enterprise-architecture/the-anthropology-of-data.html
C1: http://www.billboard.com/articles/news/7949029/taylor-swift-look-what-you-made-me-do-timeline-reputation

Engaging students: Factoring polynomials

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Brittnee Lein. Her topic, from Algebra: factoring polynomials.

1. How can technology be used to effectively engage students with this topic?

There are many great websites that can help to provide students a conceptual framework for factoring polynomials in lieu of simple lecture. This website lets students explore polynomial equations with online algebra tiles.

https://illuminations.nctm.org/activity.aspx?id=3482

Algebra tiles are effective in teaching factoring because they provide a visual representation of abstract concepts and allow students to understand that the symbol “=” in an equation really means equivalence (i.e. what you do to one side of the equation, you must do to the other side). I also think algebra tiles are very beneficial in teaching students about zero pairs. There are other websites –such as wolfram alpha– that are especially great supplements to go alongside topics such as factoring polynomials because students can see the graphical meaning of the roots of a quadratic equation. When combined, these websites can aid students in gaining a both conceptual and procedural understanding of the topic.

How could you as a teacher create an activity or project that involves your topic?

There is an activity called “Factor Draft” where students set up a ‘playing field’ of cards. In this field, there are factor cards such as (x+2), (x-12), etc. sum (5x), (12x), etc., and product cards (1), (42), and so on. The goal of the game is to draw a winning hand of two factor cards and a corresponding sum and product card. Each card is color coded to their type. Each turn a player draws one card from the field of face up cards. The player must pay mind to not only his/her own cards but also those of their opponent’s –as the first person to get two factor cards and their corresponding sum and product card wins. This activity is beneficial in furthering student understanding between the relationships between each term in a quadratic polynomial. For example $(x+4)(x-3) = x^2 + 1x - 12$ and the corresponding factor cards would be (x+4) and (x-3) the sum card would be (1x) and the product card would be (-12). This activity allows students to intuitively get a sense of the process of factoring and gives them practice multiplying out polynomials.

2. How can this topic be used in your students’ future courses in mathematics or science?
• Factoring polynomials is used in many important future science and mathematics concepts. When a quadratic equation cannot be factored simply, teachers must introduce the quadratic formula. This slides into the introduction of complex roots of an equation and complex numbers. When factoring polynomials of higher degree than 2, synthetic division (another topic in high school mathematics) is useful in finding the roots of the equation. If a student is able to understand the meaning of the roots of an equation, that will aid in solving many interesting physics and mathematics problems. Factoring is used quite often to find the domain of a rational equation such as $f(x) = (x+2)/ (x^2+ 4x+3)$ . A student must also have a strong basis in factoring polynomials to learn concepts such as completing the square.

References

• National Library of Virtual Manipulatives, nlvm.usu.edu/en/nav/vlibrary.html.

• Cleveland, James. “The Factor Draft.” The Roots of the Equation, 23 May 2014, rootsoftheequation.wordpress.com/2014/05/22/the-factor-draft/.