The following problem appeared in Volume 131, Issue 9 (2024) of The American Mathematical Monthly.
Let
and
be independent normally distributed random variables, each with its own mean and variance. Show that the variance of
conditioned on the event
is smaller than the variance of
alone.
Not quite knowing how to start, I decided to begin by simplifying the problem and assume that both and
follow a standard normal distribution, so that
and
. After solving this special case, I then made a small generalization by allowing
to be arbitrary. Solving these two special cases boosted my confidence that I would eventually be able to tackle the general case, which I start to consider with this post.
We suppose that ,
,
, and
. The goal is to show that
.
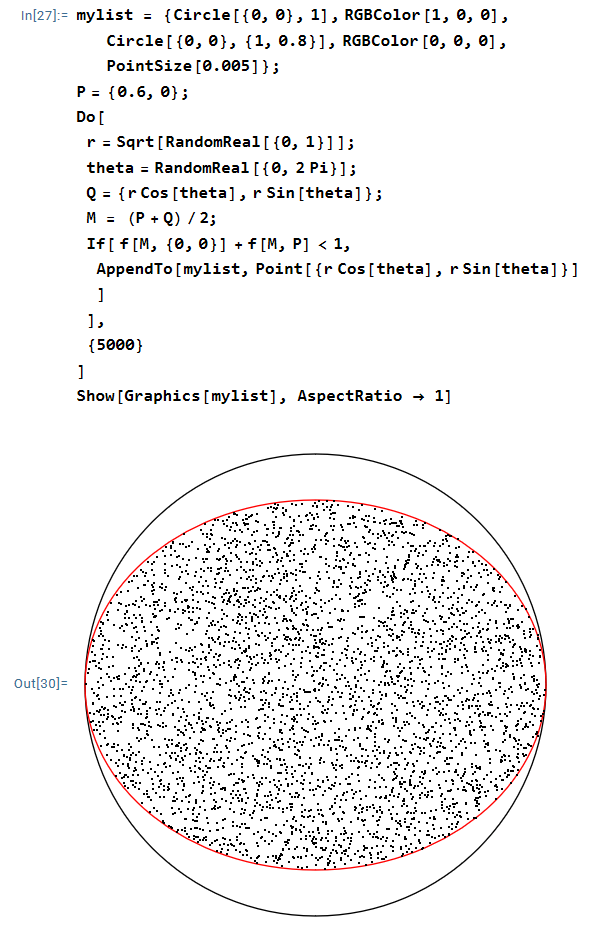
Based on the experience of the special cases, it seems likely that I’ll eventually need to integrate over the joint probability density function of and
. However, it’s a bit easier to work with standard normal random variables than general ones, and so I wrote
and
, where
and
are independent standard normal random variables.
We recall that
,
and so we’ll have to compute . We switch to
and
:
,
where we define and
for the sake of simplicity. Since
and
are independent, we know that
will also be a normal random variable with
and
.
Therefore, converting to standard units,
,
where and
is the cumulative distribution function of the standard normal distribution.
We already see that the general case is more complicated than the two special cases we previously considered, for which was simply equal to
.
In future posts, we take up the computation of and
.