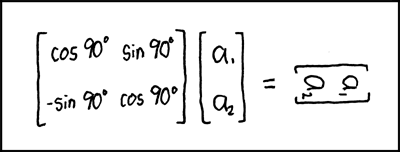Tag: xkcd

Factoring the time

factoring_the_time

True story: one way that I commit large numbers to (hopefully) short-term memory is by factoring. If I take the time to factor a big number, then I can usually remember it for a little while.

This approach has occasional disadvantages. For example, I now have stuck in my brain the completely useless information that, many years ago, my seat at a Texas Rangers ballgame was somewhere in Section 336 (which is 6 \times 7 \times 8).

Source: http://www.xkcd.com/247/

Unsolved problems: the Collatz conjecture

Students at all levels — elementary, middle, secondary, and college — tend to think that either (1) all the problems in mathematics have already been solved, or else (2) some unsolved problems remain but only an expert can understand even the statement of the problem.

There are plenty of famous unsolved problems in mathematics. And the Collatz conjecture is an easily stated unsolved problem that can be understood by most fourth and fifth graders.

Here’s the statement of the problem.

  • Start with any positive integer.
  • If the integer is even, divide it by 2. If it’s odd, multiply it by 3 and then add 1.
  • Repeat until (and if) you reach 1.

That’s it. From Wikipedia:

For instance, starting with 6, one gets the sequence 6, 3, 10, 5, 16, 8, 4, 2, 1.

Starting with 11, for example, takes longer to reach 1: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

The sequence for 27 takes 111 steps, climbing to 9232 before descending to 1: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1

The longest progression for any initial starting number less than 100 million is 63,728,127, which has 949 steps. For starting numbers less than 1 billion it is 670,617,279, with 986 steps, and for numbers less than 10 billion it is 9,780,657,630, with 1132 steps.

Here’s the question: Does this sequence eventually reach 1 no matter the starting value? Or is there a number out there that you could use as a starting value that has a sequence that never reaches 1?

Like I said, this is an easily stated problem that most fourth graders could understand. And no one knows the answer. Every number that’s been tried by computer has produced a sequence that eventually reaches 1. But that doesn’t mean that there isn’t a bigger number out there that doesn’t reach 1.

I’ll refer to the above Wikipedia page (and references therein) for further reading about the Collatz conjecture. Pedagogically, I suggest that casually mentioning this unsolved problem in class might inspire students to play with mathematics on their own, rather than think that all of mathematics has already been solved by somebody.

xkcdcollatz_conjecture

Source: http://www.xkcd.com/710/

Statistical significance

When teaching my Applied Statistics class, I’ll often use the following xkcd comic to reinforce the meaning of statistical significance.

significant

The idea that’s being communicated is that, when performing an hypothesis test, the observed significance level P is the probability that the null hypothesis is correct due to dumb luck as opposed to a real effect (the alternative hypothesis). So if the significance level is really about 0.05 and the experiment is repeated about 20 times, it wouldn’t be surprising for one of those experiments to falsely reject the null hypothesis.

In practice, statisticians use the Bonferroni correction when performing multiple simultaneous tests to avoid the erroneous conclusion displayed in the comic.

Source: http://www.xkcd.com/882/