Calculators and complex numbers (Part 8)

In this series of posts, I explore properties of complex numbers that explain some surprising answers to exponential and logarithmic problems using a calculator (see video at the bottom of this post). These posts form the basis for a sequence of lectures given to my future secondary teachers.

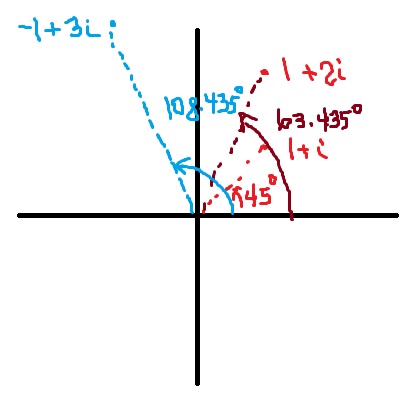
To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

where $r = |z| = \sqrt{a^2 + b^2}$ and $\tan \theta = b/a$ , with $\theta$ in the appropriate quadrant. As noted before, this is analogous to converting from rectangular coordinates to polar coordinates.

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

In the previous three posts, we discussed De Moivre’s Theorem:

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

Let’s now use this theorem to solve an algebraic equation.

Find all $z$ so that $z^3 = -27$ .

When I present this to my students, their kneejerk reaction is always to answer “ $-3$ .” To which I politely point out, “This is a cubic equation. So how many roots does it have?” Of course, they answer “Three.” To which I respond, “OK, so how do we find the other two roots?”

With enough patience, a student will usually volunteer that $z^3 + 27 = 0$ has a known root of $z = -3$ , and so the remaining roots can be found using synthetic division by dividing $z+3$ into $z^3 + 27$ , yielding

$z^3 + 27 = (z+3)(z^2 - 3z + 9)$

So the other two roots can be found using the quadratic formula:

$z = \displaystyle \frac{3 \pm \sqrt{9 - 36}}{2} = \displaystyle \frac{3}{2} \pm \frac{3\sqrt{3}}{2} i$

So there are indeed three roots. Though I usually won’t take class time to do it, I encourage my students to cube these two answers to confirm that they indeed get $-27$ .

As an aside, before moving on to the use of De Moivre’s Theorem, I usually point out to my students that there is a formula for factoring the sum of two cubes:

$a^3 + b^3 = (a+b)(a^2 - ab + b^2)$

And there’s a formula for the difference of two cubes:

$a^3 - b^3 = (a-b)(a^2 + ab + b^2)$

My experience is that even math majors are not familiar with these two formulas. They know the difference of two squares formula, but they’re either not proficient with these two formulas or else they’ve never seen them before. These can be generalized for any odd positive exponent and any positive exponent, respectively.

In tomorrow’s post, I’ll describe how these three roots can be found by using De Moivre’s Theorem.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 7)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

This post builds off the previous two posts by completing the proof of De Moivre’s Theorem.

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

The proof has two parts:

For $n \ge 0$ : proof by induction.
For $n < 0$ : let $n = -m$ , and then use part 1.

In the previous post, I presented how I describe the proof of step 1 to students. Today, I’ll discuss how I present step 2.

My personal opinion is that the proof of step 2 goes easiest when a numerical example is done first. Let $n = -5$ . Students can usually volunteer the successive steps of this special case:

$\left[ r (\cos \theta + i \sin \theta) \right]^{-5} = \displaystyle \frac{1}{ \left[ r (\cos \theta + i \sin \theta) \right]^{5} }$

$= \displaystyle \frac{1}{r^5 (\cos 5 \theta + i \sin 5 \theta)}$

At this point, students usually want to multiply by the conjugate of the denominator. There’s nothing wrong with doing that, of course, but it’s more elegant to write the numerator in trigonometric form:

$= \displaystyle \frac{1(\cos 0 + i \sin 0)}{r^5 (\cos 5 \theta + i \sin 5 \theta)}$

$= r^{-5} (\cos [0-5\theta] + i \sin[0-5\theta] )$

$= r^{-5} (\cos [-5\theta] + i \sin[ - 5\theta])$ ,

which matches what we would have expected. Students are now prepared for the proof, which I try to place alongside the above computation for $n = -5$ .

Proof for $n < 0$ . Let $n = -m$ . I tell students to imagine that $n$ is $-5$ , so that $m$ is equal to (students volunteer) $5$ . In other words, $n$ is negative and $m$ is positive. Then

$\left[ r (\cos \theta + i \sin \theta) \right]^{n} = \displaystyle \frac{1}{ \left[ r (\cos \theta + i \sin \theta) \right]^{-n} }$

I again remind everyone that $-n = m$ is positive, and so (like a good MIT freshman) the previous work applies:

$= \displaystyle \frac{1}{ \left[ r (\cos \theta + i \sin \theta) \right]^m }$

The remaining steps mirror the calculation above:

$= \displaystyle \frac{1}{r^m (\cos m \theta + i \sin m \theta)}$

$= \displaystyle \frac{1(\cos 0 + i \sin 0)}{r^m (\cos m \theta + i \sin m \theta)}$

$= r^{-m} (\cos [0-m\theta] + i \sin[0-m\theta] )$

$= r^{-m} (\cos [-m\theta] + i \sin[ - m \theta])$

$= r^{n} (\cos [n\theta] + i \sin[ n \theta])$ ,

thus ending the proof. green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 6)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

In the previous post, I used a numerical example to justify De Moivre’s Theorem:

Theorem. If $n$ is an integer, then $\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

The proof has two parts:

For $n \ge 0$ : proof by induction.
For $n < 0$ : let $n = -m$ , and then use part 1.

In this post, I describe how I present part 1 to students in class. The next post will cover part 2. As noted before, I typically present this theorem and its proof after a numerical example so that students can guess the statement of the theorem on their own.

Proof for $n \ge 0$ .

Base Case: $n = 0$ . This is trivial, as the left-hand side is

$\left[ r (\cos \theta + i \sin \theta) \right]^0 = 1$ ,

while the right-hand side is

$r^0 (\cos 0 \theta + i \sin 0 \theta) = 1(\cos 0 + i \sin 0) = 1(1 + 0i) = 1$ .

Assumption. We now assume, for a given integer $latex $n$, that

$\left[ r (\cos \theta + i \sin \theta) \right]^n = r^n (\cos n \theta + i \sin n \theta)$ .

Inductive Step. We now use the above assumption to prove the statement for $n+1$ . On the board, I write the left-hand side on the top and the right-hand side on the bottom, leaving plenty of space in between:

$\left[ r (\cos \theta + i \sin \theta) \right]^{n+1}$

$\quad$

$= r^{n+1} (\cos [n+1] \theta + i \sin [n+1] \theta)$ .

All we have to do is fill in the space to transform the left-hand side into the target on the right-hand side. (I like to call the right-hand side “the target,” as it suggests the direction in which the proof should aim.) I also tell the class that we’re more than two-thirds done with the proof, since we’ve finished the first two steps and have made some headway on the third. This usually produces knowing laughter since the hardest part of the proof is creatively converting the left-hand side into the target.

The first couple steps of the proof are usually clear to students:

$\left[ r (\cos \theta + i \sin \theta) \right]^{n+1} = \left[ r (\cos \theta + i \sin \theta) \right]^n \cdot \left[ r (\cos \theta + i \sin \theta) \right]$

$= \left[ r^n (\cos n \theta + i \sin n \theta) \right] \cdot \left[ r (\cos \theta + i \sin \theta) \right]$

by induction hypothesis. (I’ll also remind students that, as a general rule, when doing a proof by induction, it’s important to actually use the inductive assumption someplace.) At this point, most students want to distribute to get the right answer. This will eventually produce the correct answer using trig identities. However, I again try to encourage them to think like MIT freshmen and use previous work. After all, the distances multiply and the angles add, so the next step can be

$=r^n \cdot r (\cos [n \theta + \theta] + i \sin [n \theta + \theta])$

$= r^{n+1} (\cos [n+1]\theta + i \sin [n+1]\theta)$ .

In tomorrow’s post, I’ll talk about how I present the second part of the proof to my students.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 5)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

The trigonometric form of a complex number permits a geometric interpretation of multiplication, given in the following theorem.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

While this theorem doesn’t seem all that helpful — just multiplying complex numbers seems easier — this theorem will be a great help for the following problem:

Compute $(\sqrt{3} + i)^{2014}$ . (When teaching this in class, I usually choose the exponent to be the current year.)

Let’s discuss the options for evaluating this expression.

Method #1: Multiply it out. (Students reflexively wince in pain — or knowing laughter — when I make this suggestion.)

Method #2: Use the 2014th row of Pascal’s triangle. (More pain and/or laughter.)

Method #3: Use the above theorem. It’s straightforward to write $\sqrt{3} + i$ as $2 \displaystyle \left( \cos \frac{\pi}{6} + i \sin \frac{\pi}{6} \right)$ … for reasons that will become apparent later, I tell my students that I’ll use radians and not degrees for this one. Most students can recognize — and this is important, before I formally prove De Moivre’s Theorem — that they need to multiply $2$ by itself 2014 times and add $\displaystyle \frac{\pi}{6}$ to itself 2014 times. Therefore,

$(\sqrt{3} + i)^{2014} = \displaystyle 2^{2014} \left( \cos \frac{2014\pi}{6} + i \sin \frac{2014\pi}{6} \right) = \displaystyle 2^{2014} \left( \cos \frac{1007\pi}{3} + i \sin \frac{1007\pi}{3} \right)$

I then try to coax my students to compute $\displaystyle \cos \frac{1007\pi}{3}$ without a calculator. With some prodding, they’ll recognize that $\displaystyle \frac{1007}{3} = \displaystyle {335}\frac{2}{3}$ , and so they can subtract $334\pi$ (not $335\pi$ ) without changing the values of sine and cosine. Therefore,

$(\sqrt{3} + i)^{2014} = \displaystyle 2^{2014} \left( \cos \frac{5\pi}{3} + i \sin \frac{5\pi}{3} \right)$

$= 2^{2014} \left( \frac{1}{2} - i \frac{\sqrt{3}}{2} \right)$

$= 2^{2013} (1-i\sqrt{3})$

By this point, students absolutely believe that the trigonometric form of a complex number serves a useful purpose. Also, this numerical example has prepared students for the formal proof of DeMoivre’s Theorem, which will be the subject of the next two posts.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 4)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

In the previous post, I proved the following theorem which provides a geometric interpretation for multiplying complex numbers.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

Perhaps unsurprisingly, there’s also a theorem for dividing complex numbers. Students can using guess the statement of this theorem.

Theorem. $\displaystyle \frac{ r_1 (\cos \theta_1 + i \sin \theta_1) }{ r_2 (\cos \theta_2 + i \sin \theta_2) } = \displaystyle \frac{r_1}{r_2} (\cos [\theta_1-\theta_2] + i \sin [\theta_1-\theta_2])$ .

Proof. The proof begins by separating the $r_1$ and $r_2$ terms and then multiplying by the conjugate of the denominator:

$\displaystyle \frac{ r_1 (\cos \theta_1 + i \sin \theta_1) }{ r_2 (\cos \theta_2 + i \sin \theta_2) }$

$= \displaystyle \frac{r_1}{r_2} \cdot \frac{ \cos \theta_1 + i \sin \theta_1 }{ \cos \theta_2 + i \sin \theta_2 } \cdot \frac{ \cos \theta_2 - i \sin \theta_2 }{ \cos \theta_2 - i \sin \theta_2 }$

$= \displaystyle \frac{r_1}{r_2} \cdot \frac{ (\cos \theta_1 + i \sin \theta_1)( \cos \theta_2 - i \sin \theta_2) } {\cos^2 \theta_2 - i^2 \sin^2 \theta_2}$

$= \displaystyle \frac{r_1}{r_2} \cdot \frac{ (\cos \theta_1 + i \sin \theta_1)( \cos \theta_2 - i \sin \theta_2) } {\cos^2 \theta_2 + \sin^2 \theta_2}$

$= \displaystyle \frac{r_1}{r_2} (\cos \theta_1 + i \sin \theta_1)( \cos \theta_2 - i \sin \theta_2)$

At this juncture in the proof, there are two legitimate ways to proceed.

Method #1: Multiply out the right-hand side. After all, this is how we proved the theorem yesterday. For this reason, students naturally gravitate toward this proof, and the proof works after recognizing the trig identities for the sine and cosine of the difference of two angles.

However, this isn’t the most elegant proof.

Method #2: I break out my old joke about the entrance exam at MIT and the importance of using previous work. I rewrite the right-hand side as

$= \displaystyle \frac{r_1}{r_2} (\cos \theta_1 + i \sin \theta_1)( \cos [-\theta_2] + i \sin [-\theta_2])$ ;

this also serves as a reminder about the odd/even identities for sine and cosine, respectively. Then students observe that the right-hand side is just a product of two complex numbers in trigonometric form, and so the angle of the product is found by adding the angles.

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 3)

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

Why is this important? When students first learn to multiply complex numbers like $1+i$ and $2+i$ , they are taught to just distribute (or, using the nomenclature that I don’t like, FOIL it out):

$(1+i)(1+2i) = 1 + 2i + i + 2i^2 = 1 + 3i - 2 = -1 + 3i$ .

The trigonometric form of a complex number permits a geometric interpretation of multiplication, given in the following theorem.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

Proof. As above, we distribute (except for the $r_1$ and $r_2$ terms):

$\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right]$

$= r_1 r_2 (\cos \theta_1 \cos \theta_2 + i \cos \theta_1 \sin \theta_2 + i \sin \theta_1 \cos \theta_2 + i^2 \sin \theta_1 \sin \theta_2$

$= r_1 r_2 (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 + i[ \sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2])$

$= r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

When actually doing this in class, the big conceptual jump for students is the last step. So I make a big song-and-dance routine out of this:

Cosine of the first times cosine of the second minus sine of the first times sine of the second… where have I seen this before?

The idea is for my students to search deep into their mathematical memories until they recall the appropriate trig identity.

For the original multiplication problem, we see that

$1+i = \sqrt{2} \left( \cos 45^\circ + i \sin 45^\circ \right)$

$1 + 2i = \sqrt{5} \left( \cos[\tan^{-1} 2] + i \sin[\tan^{-1} 2] \right) \approx \sqrt{5} \left( \cos 63.435^\circ + i \sin 63.435^\circ \right)$

Therefore, the product of $1+i$ and $1+2i$ will be a distance of $\sqrt{2} \cdot \sqrt{5} = \sqrt{10}$ from the origin, and the angle from the positive real axis will be $45^\circ + \tan^{-1} 2 \approx 45^\circ + 63.435^\circ = 108.435^\circ$ . Indeed,

$-1 + 3i \approx \sqrt{10} \left( \cos 108.435^\circ + i \sin 108.435^\circ \right)$ .

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Two ways of doing an integral (Part 2)

A colleague placed the following problem on an exam, expecting the following solution:

$\displaystyle \int \frac{dx}{\sqrt{4x-x^2}} = \sin^{-1} \left( \displaystyle \frac{x-2}{2} \right) + C$

However, one student produced the following solution (see yesterday’s post for details):

$\displaystyle \int \frac{dx}{\sqrt{4x-x^2}} = 2 \sin^{-1} \left( \displaystyle \frac{\sqrt{x}}{2} \right) + C$

As he couldn’t find a mistake in the student’s work, he assumed that the two expressions were equivalent. Indeed, he differentiated the student’s work to make sure it was right. But he couldn’t immediately see, using elementary reasoning, why they were equivalent. So he walked across the hall to my office to ask me if I could help.

Here’s how I showed they are equivalent.

Let $\alpha = \displaystyle \sin^{-1} \left( \frac{x-2}{2} \right)$ and $\beta = \sin^{-1} \left( \displaystyle \frac{\sqrt{x}}{2} \right)$ . Then

$\displaystyle \sin(\alpha - 2\beta) = \sin \alpha \cos 2\beta - \cos \alpha \sin 2\beta$ .

Let’s evaluate the four expressions on the right-hand side.

First, $\sin \alpha$ is clearly equal to $\displaystyle \frac{x-2}{2}$ .

Second, $\cos 2\beta = 1 - 2 \sin^2 \beta$ , so that

$\cos 2\beta = \displaystyle 1 - 2\left( \frac{\sqrt{x}}{2} \right)^2 = \displaystyle 1 - \frac{x}{2} = \displaystyle -\frac{x-2}{2}$ .

Third, to evaluate $\cos \alpha$, I’ll use the identity $\displaystyle \cos \left( \sin^{-1} x \right) = \sqrt{1 - x^2}$ :

$\cos \alpha = \displaystyle \sqrt{1 - \left( \frac{x-2}{2} \right)^2 } = \displaystyle \frac{\sqrt{4x-x^2}}{2}$

Fourth, $\sin 2\beta = 2 \sin \beta \cos \beta$ . Using the above identity again, we find

$\sin 2\beta = \displaystyle 2 \left( \frac{ \sqrt{x} }{2} \right) \sqrt{ 1 - \left( \frac{ \sqrt{x} }{2} \right)^2 }$

$= \sqrt{x} \sqrt{1 - \displaystyle \frac{x}{4}}$

$= \displaystyle \frac{\sqrt{4x-x^2}}{2}$

Combining the above, we find

$\sin(\alpha - 2 \beta) = \displaystyle -\left( \frac{x-2}{2} \right)^2 - \left( \frac{\sqrt{4x-x^2}}{2} \right)^2$

$\sin(\alpha - 2 \beta) = \displaystyle \frac{-(x^2 - 4x + 4) - (4x - x^2)}{4}$

$\sin(\alpha - 2 \beta) = -1$

$\alpha - 2 \beta = \displaystyle -\frac{\pi}{2} + 2\pi n$ for some integer $n$

Also, since $-\pi/2 \le \alpha \le \pi/2$ and $0 \le -2\beta \le \pi$ , we see that $-\pi/2 \le \alpha - 2 \beta \le 3\pi/2$ . (From its definition, $\beta$ is the arcsine of a positive number and therefore must be nonnegative.) Therefore, $\alpha - 2\beta = -\pi/2$ .

In other words,

$\sin^{-1} \left( \displaystyle \frac{x-2}{2} \right)$ and $2 \sin^{-1} \left( \displaystyle \frac{\sqrt{x}}{2} \right)$

differ by a constant, thus showing that the two antiderivatives are equivalent.

Trig identity

Why do we still require students to rationalize denominators?

Which answer is simplified: $\displaystyle \frac{1}{2 \sqrt{2}}$ or $\displaystyle \frac{ \sqrt{2} }{4}$ ? From example, here’s a simple problem from trigonometry:

Suppose $\theta$ is an acute angle so that $\sin \theta = \displaystyle \frac{1}{3}$ . Find $\tan \theta$ .

To solve, we make a right triangle whose side opposite of $\theta$ has length $1$ and hypotenuse with length $3$ . The adjacent side has length $\sqrt{3^2 - 1^2} = \sqrt{8} = 2\sqrt{2}$ . Therefore,

$\tan \theta = \displaystyle \frac{ \hbox{Opposite} }{ \hbox{Adjacent} } = \displaystyle \frac{1}{2 \sqrt{2}}$

This is the correct answer, and it could be plugged into a calculator to obtain a decimal approximation. However, in my experience, it seems that most students are taught that this answer is not yet simplified, and that they must rationalize the denominator to get the “correct” answer:

$\tan \theta = \displaystyle \frac{1}{2 \sqrt{2}} \cdot \frac{ \sqrt{2} }{ \sqrt{2} } = \displaystyle \frac{ \sqrt{2} }{4}$

Of course, this is equivalent to the first answer. So my question is philosophical: why are students taught that the first answer isn’t simplified but the second is? Stated another way, why is a square root in the numerator so much more preferable than a square root in the denominator?

Feel free to correct me if I’m wrong, but it seems to me that rationalizing denominators is a vestige of an era before cheap pocket calculators. Let’s go back in time to an era before pocket calculators… say, 1927, when The Jazz Singer was just released and stars of silent films, like Don Lockwood, were trying to figure out how to act in a talking movie.

Before cheap pocket calculators, how would someone find $\displaystyle \frac{1}{2 \sqrt{2}} ~~$ or $~~ \displaystyle \frac{ \sqrt{2} }{4}$ to nine decimal places? Clearly, the first step is finding $\sqrt{2}$ by hand, which I discussed in a previous post. So these expressions reduce to

$\displaystyle \frac{1}{2 (1.41421356\dots)}$ or $\displaystyle \frac{1.41421356\dots}{4}$

Next comes the step of dividing. If you don’t have a calculator and had to use long division, which would rather do: divide by $4$ or divide by $2.82842712\dots$ ?

Clearly, long division with $4$ is easier.

It seems to me that ease of computation was the reason that rationalizing denominators was required of students in previous generations. So I’m a little bemused why rationalizing denominators is still required of students now that cheap calculators are so prevalent.

Lest I be misunderstood, I absolutely believe that all students should be able to convert $\displaystyle \frac{1}{2 \sqrt{2}}$ into $\displaystyle \frac{ \sqrt{2} }{4}$ . But I see no compelling reason why the “simplified” answer to the above trigonometry problem should be the second answer and not the first.

Engaging students: right-triangle trigonometry

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Kelsie Teague. Her topic, from Precalculus: right-triangle trigonometry.

How has this topic appeared in popular culture?

In the famous T.V. show Numbers they do an episode using trig to find the angle of origin of the blood spatter. In forensic science they use trig every day to determine where the victim was originally injured. They can also use this to find the angle of impact, area/point of convergence, and area of origin. The following power point goes into more detail: http://cmb.physics.wisc.edu/people/gault/Blood%20Splatter%20Trig.pdf

If the blood was dropped by a 90-degree angle, the stain will appear to be an almost perfect circle.

We could get out some long paper and colored water and experiment with the idea of change of angle in the drop of blood and calculate the angles.

Angle of Impact =Sin (theta)= Width of drop/Length of drop.

How can technology (YouTube, Khan Academy [khanacademy.org], Vi Hart, Geometers Sketchpad, graphing calculators, etc.) be used to effectively engage students with this topic?

YouTube is a great website for engagement because you can find many videos to start the lesson off with some previous knowledge that they will be using for that days lesson. The following video would be a good way to engage the students when talking about right triangle trig.

It’s to a song that they probably have already heard and it’s teaching them something they already know. Since the students already have knowledge of this, the video isn’t teaching them the topic but refreshing their memory in a entertaining fashion.

When looking for a good video, I ran across many that would work for this lesson, but this one seemed like it would grab the student’s attention more and keep their attention.

The above video is also a good one, and it shows the lyrics in the description so you can make sure what they are saying is mathematically correct so it doesn’t give the students any misconceptions.

How could you as a teacher create an activity or project that involves your topic?

If I was teaching at a school that was close to a hill or a mountain outside I could take my students outside and have them figure out how far up the mountain they would have to walk to get to the top. We could use a tap measure to measure how high they had the protractor in the air and then we could look up the height and distance away of the mountain. They then could use the protractor to find the angle between themselves and the top of the mountain. We could then use this information inside the classroom to solve how far to travel up the mountain.

Similar to the above picture except they will know the height of the mountain. This would show the length of the hypotenuse of the right triangle. They will have to subtract the height they have the protractor at from the height of the mountain to be accurate since the height of the mountain is from the ground up.