In the previous posts of this series, I described two methods of deriving the formula

The first method concerned reversing the terms of the sum (or, almost equivalently, taking the terms in pairs). The second method used mathematical induction.
Mathematical induction can be applied to arithmetic series as well as other series. However, the catch is that you have to know the answer before proving that the answer actually is correct. By contrast, the first method did not require us to know the answer in advance — it just fell out of the calculation — but it cannot be applied to series that are not arithmetic.
Here’s a third method using the principle of telescoping series. This method has the strengths of the previous two methods: it does not require us to know the answer in advance, and it can also be applied to some other series which are not arithmetic.
To begin, consider the sum
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D&bg=ffffff&fg=000000&s=0&c=20201002)
At this early point, students often object, “Where did that come from?” I’ve said it before but I’ll say it again: I tell them my usual tongue-in-cheek story that this idea comes from the patented Bag of Tricks. Socrates gave the Bag of Tricks to Plato, Plato gave it to Aristotle, it passed down the generations, my teacher taught the Bag of Tricks to me, and I teach it to my students.
In any event, I will evaluate this sum in two different ways.
Step 1. Just write out the terms of the series, starting from  and ending with
and ending with  .
.
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = [1^2 - 0^2] + [2^2 - 1^2] + [3^2 - 2^2] + \dots + [n^2 - (n-1)^2]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+%5B1%5E2+-+0%5E2%5D+%2B+%5B2%5E2+-+1%5E2%5D+%2B+%5B3%5E2+-+2%5E2%5D+%2B+%5Cdots+%2B+%5Bn%5E2+-+%28n-1%29%5E2%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Notice that, on the right-hand side, the 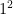 terms cancel, the
terms cancel, the  terms cancel, and so on. In fact, almost everything cancels. The only two terms that aren’t cancelled are the
terms cancel, and so on. In fact, almost everything cancels. The only two terms that aren’t cancelled are the 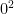 and
and 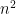 terms. Therefore,
terms. Therefore,
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = n^2 - 0^2 = n^2](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+n%5E2+-+0%5E2+%3D+n%5E2&bg=ffffff&fg=000000&s=0&c=20201002)
Step 2. Next, we’ll rewrite the original sum by expanding out the terms inside of the sum:
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = \displaystyle \sum_{k=1}^n [k^2 - (k^2 -2k + 1)]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k%5E2+-2k+%2B+1%29%5D&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = \displaystyle \sum_{k=1}^n [2k-1]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5B2k-1%5D&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = \displaystyle \sum_{k=1}^n 2k - \displaystyle \sum_{k=1}^n 1](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+2k+-+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+1&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = 2\displaystyle \sum_{k=1}^n k - \displaystyle \sum_{k=1}^n 1](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+2%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+k+-+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+1&bg=ffffff&fg=000000&s=0&c=20201002)
Step 3. Of course, these different looking answers from Steps 1 and 2 have to be the same, so let’s set them equal to each other:

There is one unknown in this equation,  . The second sum is just the constant
. The second sum is just the constant 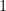 added to itself
added to itself  times, and so
times, and so 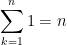 . Therefore, we solve for the unknown:
. Therefore, we solve for the unknown:



 The beauty of this approach is that this approach can be continued. For example, to obtain
The beauty of this approach is that this approach can be continued. For example, to obtain  , we begin with
, we begin with
![\displaystyle \sum_{k=1}^n [k^3 - (k-1)^3]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E3+-+%28k-1%29%5E3%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Step 1. By telescoping series,
![\displaystyle \sum_{k=1}^n [k^3 - (k-1)^3] = n^3 - 0^3 = n^3](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E3+-+%28k-1%29%5E3%5D+%3D+n%5E3+-+0%5E3+%3D+n%5E3&bg=ffffff&fg=000000&s=0&c=20201002)
Step 2. Using the binomial theorem,
![\displaystyle \sum_{k=1}^n [k^3 - (k-1)^3] = \displaystyle \sum_{k=1}^n [k^3 - (k^3 -3k^2+3k- 1)]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E3+-+%28k-1%29%5E3%5D+%3D+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E3+-+%28k%5E3+-3k%5E2%2B3k-+1%29%5D&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = 3\displaystyle \sum_{k=1}^n k^2 - 3\displaystyle \sum_{k=1}^n k + \displaystyle \sum_{k=1}^n 1](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+3%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+k%5E2+-+3%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+k+%2B+%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+1&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \sum_{k=1}^n [k^2 - (k-1)^2] = 3\displaystyle \sum_{k=1}^n k^2 - 3\left( \frac{n(n+1)}{2} \right) + n](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+%5Bk%5E2+-+%28k-1%29%5E2%5D+%3D+3%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En+k%5E2+-+3%5Cleft%28+%5Cfrac%7Bn%28n%2B1%29%7D%7B2%7D+%5Cright%29+%2B+n&bg=ffffff&fg=000000&s=0&c=20201002)
Step 3. Setting these two expressions equal to each other,

And we eventually conclude that:
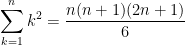
And then this could be continued to obtain closed-form expressions for higher exponents of  .
.
,
